Werner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse is also true. this is summed up in what we now call the Heisenberg uncertainty principal. The equation is Δx.Δ(mv)≥h4π
The uncertainty is the position or in the momentum of a macroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electron is small enough for the uncertainty to be relatively large and significant.
If the uncertainty in velocity and position is same, then the uncertainty in momentum will be
√hm4π
m√h4π
√h4πm
1m√h4π
The correct Answer is:A
Δx.Δp=h4π
Topper's Solved these Questions
Similar Questions
Complete the following reaction
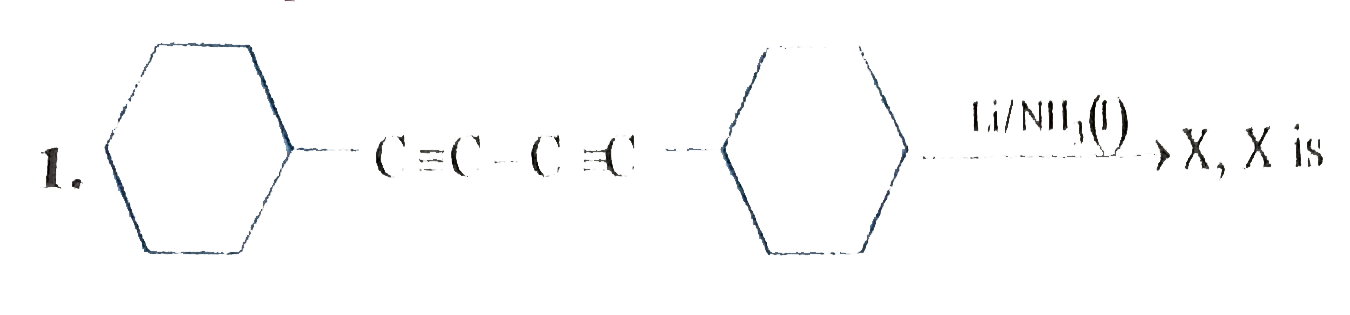
View Solution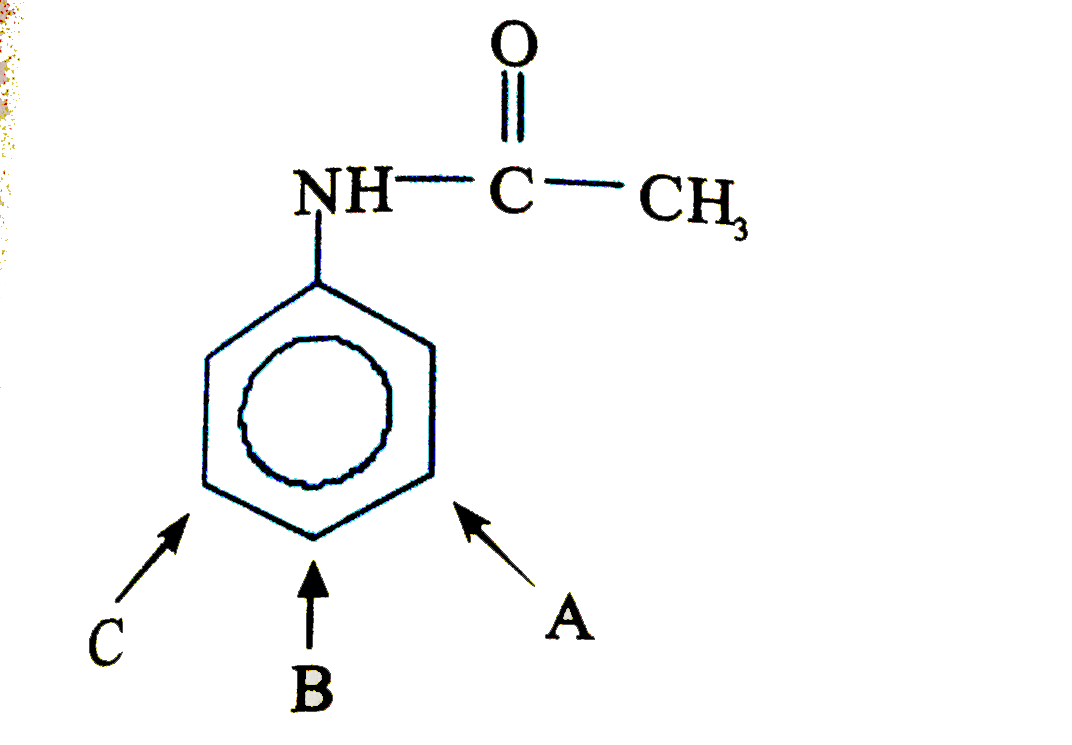
Identify the position where electrophilic aromatic substitution EAS) is most favourable
View SolutionWerner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse also true. This is summed up in what we now call the Heisenberg uncertainty principle.
The equation si δx.δ(mv)≥h4π
The uncertainty in the position or in the momentum of a marcroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electon is small enough for the uncertainty to be relatively large and significant.
If the uncertainties in position and momentum are equal, the uncertainty in the velocity is :
View SolutionWerner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse also true. This is summed up in what we now call the Heisenberg uncertainty principle.
The equation si δx.δ(mv)≥h4π
The uncertainty in the position or in the momentum of a marcroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electon is small enough for the uncertainty to be relatively large and significant.
If the uncertainty in velocity and position is same, then the uncertainty in momentum will be :
View SolutionWerner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse also true. This is summed up in what we now call the Heisenberg uncertainty principle.
The equation si δx.δ(mv)≥h4π
The uncertainty in the position or in the momentum of a marcroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electon is small enough for the uncertainty to be relatively large and significant.
What would be the minimum uncetaintty in de-Broglie wavelength of a moving electron accelerated by potential difference of 6 volt and whose uncetainty in position is 722 nm?
View SolutionWerner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse is also true. this is summed up in what we now call the Heisenberg uncertainty principal. The equation is Δx.Δ(mv)≥h4π
The uncertainty is the position or in the momentum of a macroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electron is small enough for the uncertainty to be relatively large and significant.
If the uncertainties in position and momentum are equal, the uncertainty in the velocity is:
View Solutionप्रक्कथन : एक इलेक्ट्रॉन सूक्ष्मदर्शी के द्वारा इलेक्ट्रॉन की सही स्थिति का निर्धारण किया जा सकता है।
कारण : संवेग के मापन में अनिश्चितता तथा स्थिति के मापन में अनिश्चितता का गुणनफल परिमित सीमा से कम नहीं हो सकता।
View SolutionWerner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse also true. This is summed up in what we now call the Heisenberg uncertainty principle.
The equation si δx.δ(mv)≥h4π
The uncertainty in the position or in the momentum of a marcroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electon is small enough for the uncertainty to be relatively large and significant.
If the uncertainty in velocity and position is same, then the uncertainty in momentum will be :
View SolutionIf uncertainity in position is zero, the uncertainity in momentum of an electron will be
View SolutionHiesenberg.s uricertainty principle states that it is impossible to determine simultaneously the position and momentum of a particle. He considered the limits of how precisely we can measure properties of an e^- (or)other microscopic particles like electron. The more accurately we measure the momentum of a particle, less accurately we can determine its position. The police are monitoring an automobile of mass 2.0 tons speeding along a high way. They are certain about location of the vehicle only to with in Im, what is the minimum uncertainty in the speed of the vehicle ?
View SolutionHiesenberg.s uricertainty principle states that it is impossible to determine simultaneously the position and momentum of a particle. He considered the limits of how precisely we can measure properties of an e^- (or)other microscopic particles like electron. The more accurately we measure the momentum of a particle, less accurately we can determine its position. If uncertainty in measurement of position and momentuin are equal calculate the uncertainty in velocity
View SolutionHow can we measure growth ?
View SolutionWerner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse also true. This is summed up in what we now call the Heisenberg uncertainty principle.
The equation si δx.δ(mv)≥h4π
The uncertainty in the position or in the momentum of a marcroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electon is small enough for the uncertainty to be relatively large and significant.
If the uncertainties in position and momentum are equal, the uncertainty in the velocity is :
View SolutionWerner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse also true. This is summed up in what we now call the Heisenberg uncertainty principle.
The equation si δx.δ(mv)≥h4π
The uncertainty in the position or in the momentum of a marcroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electon is small enough for the uncertainty to be relatively large and significant.
What would be the minimum uncetaintty in de-Broglie wavelength of a moving electron accelerated by potential difference of 6 volt and whose uncetainty in position is 722 nm?
View SolutionWerner Heisenberg considered the limits of how precisely we can measure the properties of an electron or other microscopic particle. He determined that there is a fundamental limit to how closely we can measure both position and momentum. The more accurately we measure the momentum of a particle, the less accurately we can determine its position. The converse also true. This is summed up in what we now call the Heisenberg uncertainty principle.
The equation si δx.δ(mv)≥h4π
The uncertainty in the position or in the momentum of a marcroscopic object like a baseball is too small to observe. However, the mass of microscopic object such as an electon is small enough for the uncertainty to be relatively large and significant.
If the uncertainties in position and momentum are equal, the uncertainty in the velocity is :
View Solution
