For a single electron atom or ion the wave number of radiation emitted during the transition of electron from a higher energy state (n=n2) to a lower energy state (n=n1) is given by the expression:
¯v=1λ=RH.z2(1n21−1n22) ...(1)
where RH=2π2mk2e4h3c= Rydberg constant for H-atom
Where the terms have their usual meanings. Considering the nuclear motion, the most accurate expression would have been to replace mass of electron (m) by the reduced mass (μ) in the above expression, defined as
μ=m'.mm'+m where m'= mass of nucleus
For Lyman series: n1=1 (fixed for all the lines)
while n2=2,3,4... for successive lines i.e. 1st,2nd,3rd... lines, respectively. For Balmer series: n1=2 (fixed for all the lines) while n2=3,4,5... for successive lines.
If proton in H-nucleus be replaced by positron having the same mass as that of electron but same charge as that of proton, then considering the nuclear motion, the wavenumber of the lowest energy transition of He+ ion in Lyman series will be equal to
2RH
3RH
4RH
RH
The correct Answer is:B
¯v=RHz2[1n21−1n22]=3RH
Topper's Solved these Questions
Similar Questions
Complete the following reaction
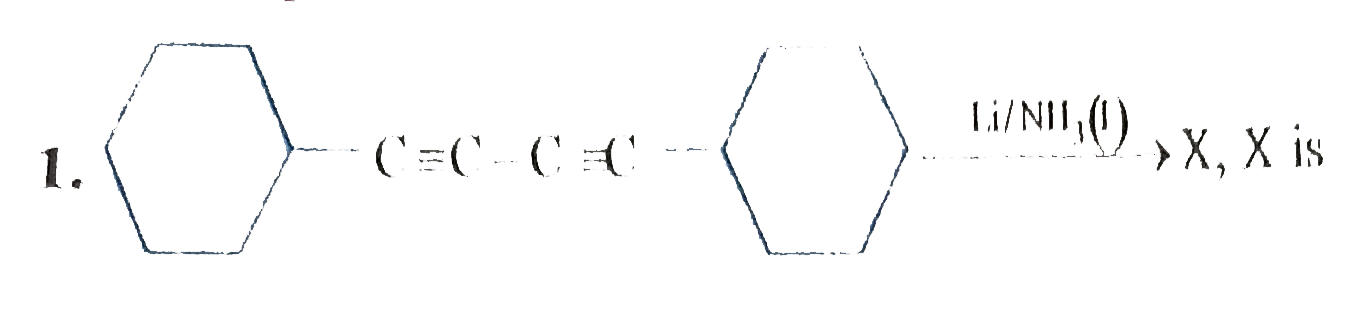
View Solution
Identify the position where electrophilic aromatic substitution EAS) is most favourable
View SolutionExcited atoms emit radiations consisting of only certain discrete frequencise or wavelengths. In spectroscopy it is often more convenient to use freuquencies and wave numbers are proportional ot energy and spectroscopy involves transitions between different energy levels . The line spectrum shown by a single electron excited atom (a finger print of an atom) can be given as 1/(lambda)=barvR_(H).Z^(2)[(1)/(n_(1)^(2))-(1)/(n_(2)^(2))] where Z is atomic number of single electron atom and n_(1),n_(2) are integers and if n_(2)gt n_(1), then emission spectrum is noticed and if n_(2)ltn_(1), then absorption spectrum is noticed. Every line in spectrum can be represented as a difference of two terms (R_(H)Z^(2))/(n_(1)^(2)) "and"(R_(H)Z^(2))/(n_(2)^(2)). H-atoms in ground state (13.6 eV) are excited by monochromatic radiations of photon of energy 12.09 eV. The number of different spectral lines emitted in H-atoms will be:
View SolutionIf n1+n2=4andn22−n21=8, then calculate maximum value of wavelength emitted in transition form n2→n1forLi2+in nm[GivenRH=107m−1].
View SolutionFor the Paschen series thr values of n_(1) and n_(2) in the expression Delta E = R_(H)c [(1)/(n_(1)^(2))-(1)/(n_(2)^(2))] are
View SolutionThe electron in a hydrogen atom makes a transition n1→n2 where n1 and n2 are the principal qunatum numbers of the two states. Assume the Bohr model to be valid. The frequency of orbital motion of the electron in the initial state is 1/27 of that in the final state. The possible values of n1 and n2 are
View SolutionFor a single electron atom or ion the wave number of radiation emitted during the transition of electron from a higher energy state (n=n2) to a lower energy state (n=n1) is given by the expression:
¯v=1λ=RH.z2(1n21−1n22) ...(1)
where RH=2π2mk2e4h3c= Rydberg constant for H-atom
Where the terms have their usual meanings. Considering the nuclear motion, the most accurate expression would have been to replace mass of electron (m) by the reduced mass (μ) in the above expression, defined as
μ=m'.mm'+m where m'= mass of nucleus
For Lyman series: n1=1 (fixed for all the lines)
while n2=2,3,4... for successive lines i.e. 1st,2nd,3rd... lines, respectively. For Balmer series: n1=2 (fixed for all the lines) while n2=3,4,5... for successive lines.
The ratio of the wave numbers for the highest energy transition of e− in Lyman and Balmer series of H-atom is:
View SolutionFor emission line of atomic hydrogen from ni=8 to nf=n, the plot of wave number (¯v) against(1n2) will be (The Rydberg constant, RH is in wave number unit)
View SolutionWhen a transition of electron in He+ takes place from n2 to n1 then wave number in terms of Rydberg constant R will be
(Given n1+n2=4,n2−n1=2)
View SolutionAccording to the Bohr theory for the atomic spectrum of hydrogen the energy levels of the proton -electron system depends, on the quantum number n. In an electron transition from a higher quantum level , n_(2) to the lower level n_(1) , radiation is emitted. The frequency, v of the radiation is given by h v = (E_(n_(2)) - E_(n_(1))) where, h is Planck.s constant and E_(n_(2)), E_(n_(1)) are the energy level values for the quantum number n_(2) and n_(1) . A useful formula for the wavelength, lambda = c//v is given by = lambda(Å) = (912)/(Z^(2)) xx ((n_(2)^(2)n_(1)^(2))/(n_(2)^(2)-n_(1)^(2))) where, Z = atomic number of any one electron species viz H, He^(+), Li^(2+), Be^(3+) ,..... For hydrogen Z=1 In the above formula, when n_(2) rarr oo , we have lambda = (912)/(1^(2)) xx n_(1)^(2) . This values of lambda is known as the series limit for the given value of n_(1) . Calculate the value of n_(1) for the series limit lambda = 8208 Å
View SolutionAccording to the Bohr theory for the atomic spectrum of hydrogen the energy levels of the proton -electron system depends, on the quantum number n. In an electron transition from a higher quantum level , n_(2) to the lower level n_(1) , radiation is emitted. The frequency, v of the radiation is given by h v = (E_(n_(2)) - E_(n_(1))) where, h is Planck.s constant and E_(n_(2)), E_(n_(1)) are the energy level values for the quantum number n_(2) and n_(1) . A useful formula for the wavelength, lambda = c//v is given by = lambda(Å) = (912)/(Z^(2)) xx ((n_(2)^(2)n_(1)^(2))/(n_(2)^(2)-n_(1)^(2))) where, Z = atomic number of any one electron species viz H, He^(+), Li^(2+), Be^(3+) ,..... For hydrogen Z=1 Calculating n_(2) for the series limit = 22800 Å. Calculate lambda for the transition (n_(2) + 1) to (n_(1) - 1)
View SolutionFor the Paschen series the values of n_(1) and n_(2) in the expression DeltaE=R_(H).c(1/(n_(1)^(2))-1/(n_(2)^(2)))
View SolutionFor emission line of atomic hydrogen from n_(i)=8 to n_(f)=n, the plot of wave number (barv) against ((1)/(n^(2))) will be (The Rydberg constant, R_(H) is in wave number unit)
View SolutionFor emission line of atomic hydrogen from ni=8 to nf=n, the plot of wave number (¯v) against(1n2) will be (The Rydberg constant, RH is in wave number unit)
View SolutionWhen a transition of electron in He+ takes place from n2 to n1 then wave number in terms of Rydberg constant R will be
(Given n1+n2=4,n2−n1=2)
View Solution
