In the Rutherford's experiment, a particles were bombarded towards the copper atoms so as to arrives a distance of 10−13 metre from the nucleus of copper and then getting either deflected or traversing back. The a-particles did not move further closer
It can also be concluded that the electrostatic potential energy is equal to
14πε0q1q2r
14πε05Ze2mv2
Ze2r
mv2
The correct Answer is:A
14πε0q1q2r
Topper's Solved these Questions
Similar Questions
With what velocity should as α- particle travel toward the nucless of a copper atom at a distance of 1013m from the nucless of the copper atom ?
View SolutionWith what velocity should an α-particle travel towards the nucleus of a Cu atom so as to arrive at a distance 10−13 metre from the nucleus of the Cu atom? (Cu=29,e=1.6×10−19C,ε0=8.85×10−12J−1C2m−1,me=9.1×10−31kg)
View Solution
Knowledge Check
In the Rutherford's experiment, a particles were bombarded towards the copper atoms so as to arrives a distance of 10−13 metre from the nucleus of copper and then getting either deflected or traversing back. The a-particles did not move further closer
The velocity of the a-particles must beA8.32×108cm/secB6.32×108cm/secC6.32×108m/secD6.32×108km/secIn the Rutherford's experiment, a particles were bombarded towards the copper atoms so as to arrives a distance of 10−13 metre from the nucleus of copper and then getting either deflected or traversing back. The a-particles did not move further closer
The velocity of the a-particles must beANαsin(+θ2)BNdσdΩα1sin4θCNdσdΩα1sin4(θ/2)DN=sin.θ2With what velocity should an α paricle travel towards the nucleus of a copper atom so as to arrive at a distance 10−13m from the nucleus of the copper atom?
A6.34×106m/secB63.4×106m/secC0.634×106m/secD6.34×10−6m/sec
Rutherford model: The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α-scattering experiment. If an α-particle is projected from infinity with speed v towards the nucleus having Z protons, then the α-particle which is reflected back or which is deflected by 180∘ must have approached closest to the nucleus .It can be approximated that α particle collides with the nucleus and gets back. Now if we apply the energy conservation equation at initial point and collision point then:
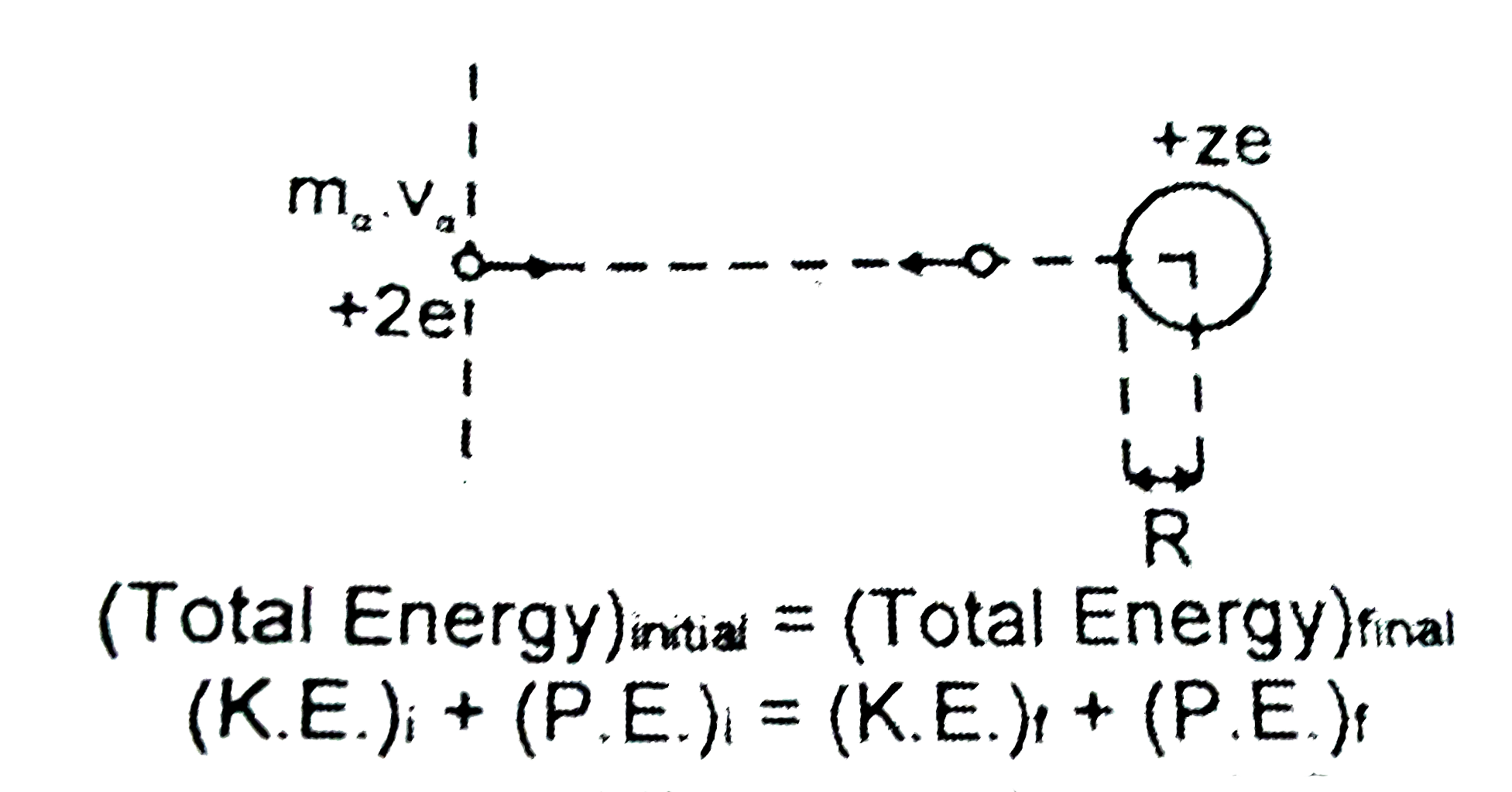
(P.E.)i=0, since P.E. of two charge system separated by infinite distance is zero. Finally the particle stops and then starts coming back.
12mαv2α+0=0+Kq1q2R⇒12mαv2α=K2e×ZeR⇒R=4KZe2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it
An α-particle with initial speed v0 is projected from infinity and it approaches up to r0 distance from a nuclie. Then, the initial speed of α-particle, which approaches upto 2r0 distance from the nucleus is :
View SolutionRead the following passage and then answer questions (a) - (e) on the basis of your understanding of the passage and the related studied concepts.
Rutherford was the pioneer who established the existence of the atomic nucleus. Result of Geiger and Marsden experiment on the scattering of a-particles from thin gold foils, performed at Rutherford’s suggestion, revealed that the distance of closest approach to a gold nucleus of an a-particle of kinetic energy 5.5 MeV is about 4.0×10−14m. The said scattering effect was explained by Rutherford by assuming that the Coulombian repulsive force was solely responsible for scattering. Since the positive charge is confined to the nucleus, the actual size of the nucleus has to be less than 4.0×10−14m.
If we use a-particles of higher energies, the distance of closest approach to the gold nucleus will be still smaller. At some point the scattering will begin to be affected by the short range nuclear forces and differ from Rutherford’s calculations. From the distance at which deviations set it, nuclear size can be inferred.
(a) Define MeV and express its value in terms of SI unit of energy.
(b) What is distance of closest approach ?
(c) Write an expression for distance of closest approach of a-particle to a gold nucleus.
(d) What was Rutherford’s hypothesis regarding the existence of the atomic nucleus ?
(e) How can you show that volume of the nucleus of an element is proportional to its mass number ?
View SolutionRead the following passage carefully and answer the questions
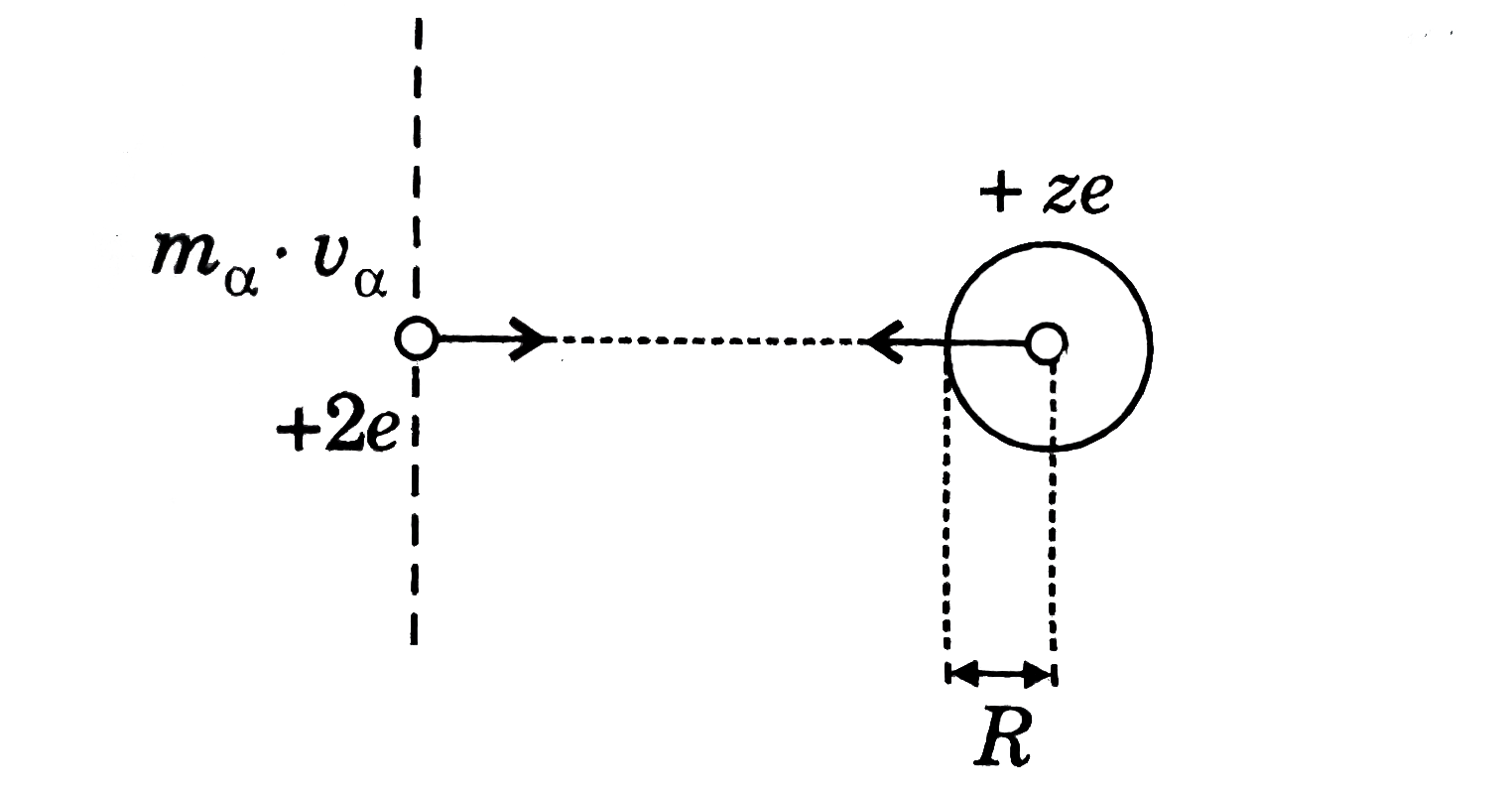
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α−scattering experiment. If an α−perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha−perticle which is reflected back or which is deflected by 180∘ must have approach closest to the nucleus. It can be approximated that α−particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
(Total Energy)initial=(Total Enregy)final
(KE)i+(PE)i=(KE)f+(PE)f
(PE)i=0,sincePE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
12mαv2α+0=0+kq1q2R
⇒12mαv2α=k2e×zeR⇒R=4kze2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
R=R0(A)1/3
where R0=1.2×10−15m
A= atomic mass number
R=radius of nucleus
If α−particle with speed v0 is projected from infinity and it approaches upto r0 distance from the nuclei. Then the speed of α−particle which approaches 2r0 distance from the nucleus is
View SolutionRead the following passage carefully and answer the questions
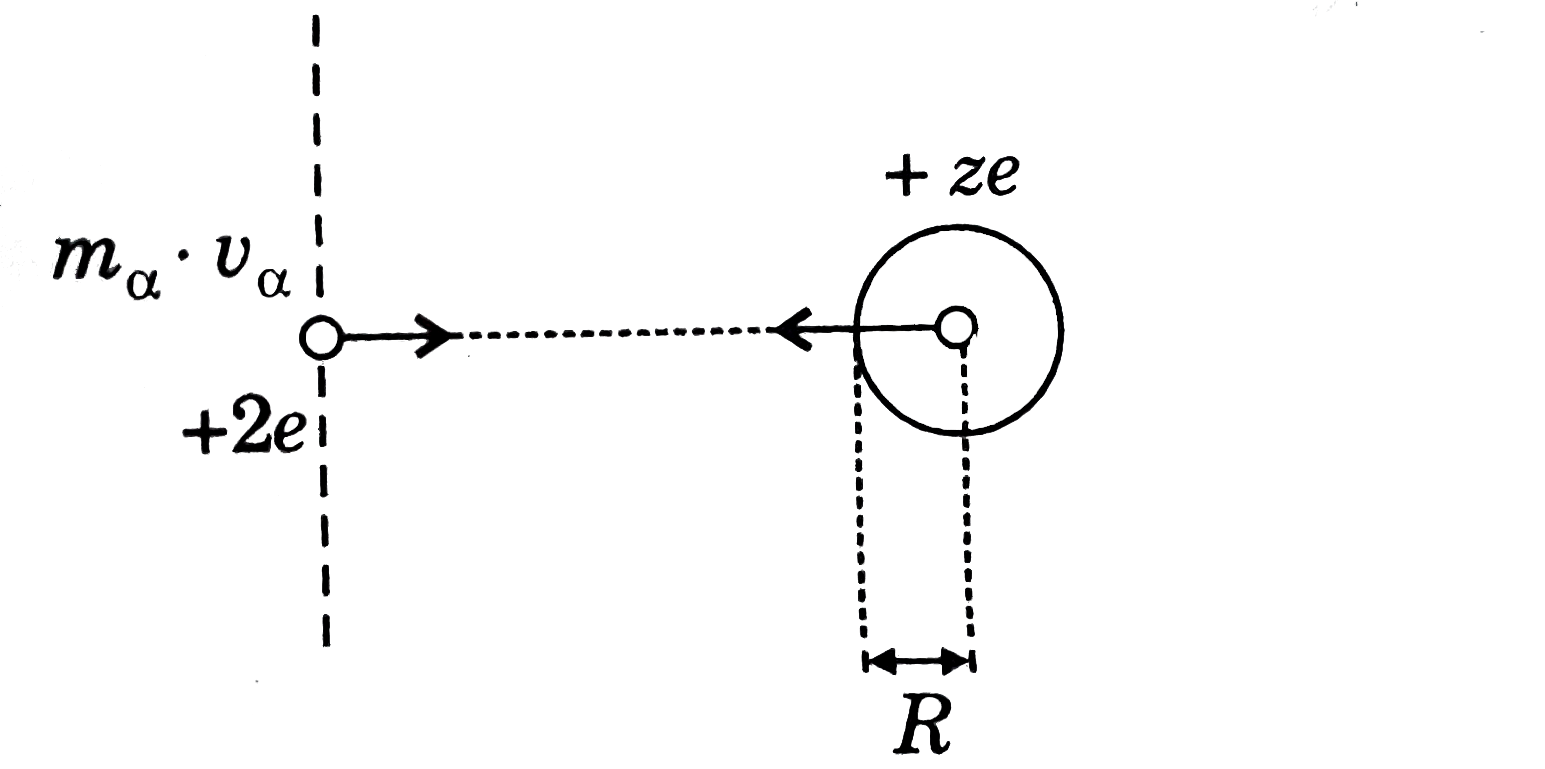
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α−scattering experiment. If an α−perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha−perticle which is reflected back or which is deflected by 180∘ must have approach closest to the nucleus. It can be approximated that α−particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
(Total Energy)initial=(Total Enregy)final
(KE)i+(PE)i=(KE)f+(PE)f
(PE)i=0,sincePE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
12mαv2α+0=0+kq1q2R
⇒12mαv2α=k2e×zeR⇒R=4kze2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
R=R0(A)1/3
where R0=1.2×10−15m
A= atomic mass number
R=radius of nucleus
Radius of a particular nucleus is calculated by the projection of α−particle from infinity at a particular speed. Let this radius be the true radius. If the radius calculation for the same nucleus is made by , α−particle with half of the earlier speed then the percentage error involved in the radius calculation is :
View SolutionThe potential energy at a point, relative to the reference point is always defined as the negative of work done by the force as the object moves from the reference point to the point considered. The value of potential energy at the reference point itself can be set equal to zero because we are always concerned only with differences of potential energy between two points and the associated change of kinetic energy. A particles A is fixed at origin of a fixed coordinate system. A particle B which is free to move experiences an force →F=(−2ar3+βr2)ˆr due to particle A where ˆr is the position vector of particle B relative to A. It is given that the force is conservative in nature and _potential energy at infinity is zero. If B has to be removed from the influence of A, energy has to be supplied for such a process. The ionization energy E 0 is work that has to be done by an external agent to move the particle from a distance r0 to infinity slowly. Here r0 is the equilibrium position of the particle
What is potential energy function of particle as function of r.
View Solution
