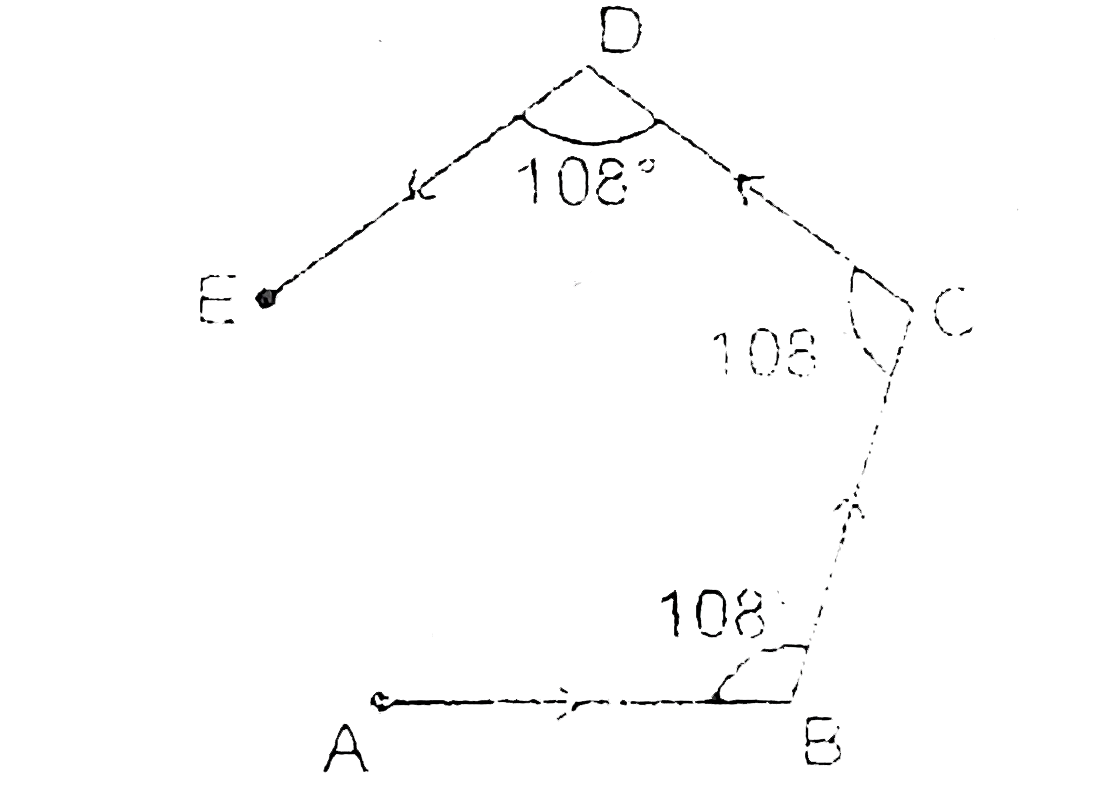
A particle moves in a plane from A to E along the shown path. It is given that Ab=BC=CD=DE=10 metre. Then the magnitude of net displacement of particle is :
 .
.
10m
15m
5m
20m
The correct Answer is:A
Appying polygon law of addition,
¯¯¯¯¯¯AB+¯¯¯¯¯¯BC+¯¯¯¯¯¯CD+¯¯¯¯¯¯DE=¯¯¯¯¯¯AE
∣∣¯¯¯¯¯¯AE∣∣=10m
Topper's Solved these Questions
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (A)
Explore 32 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART (B)
Explore 3 Videos
- TEST PAPERSBook:BANSALChapter:TEST PAPERSExercise:PHYSICS PART- C
Explore 4 Videos
- SEMICONDUCTORSBook:BANSALChapter:SEMICONDUCTORSExercise:CBSE Question
Explore 32 Videos
Similar Questions
A particle travels along the path ABC, as shown in the figure given below, AB = BC = l, calculate the path length and displacement of the particle
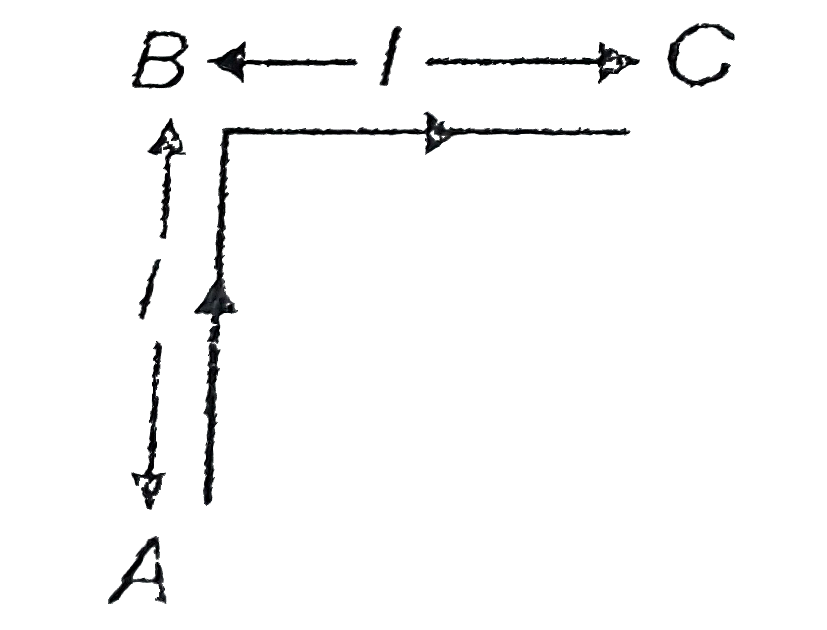
View SolutionA particle goes along a quadrant of a circle of radius 10m from A to B as shown in fig. Find the magnitude of displacement and distance along the path AB, and angle between displacement vector and x-axis ?
View Solution
Knowledge Check
A particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:
 A10mB5√2mC9mD7√2m
A10mB5√2mC9mD7√2mA particle travels from A to B path shown in figure, then the displacement of particle is :
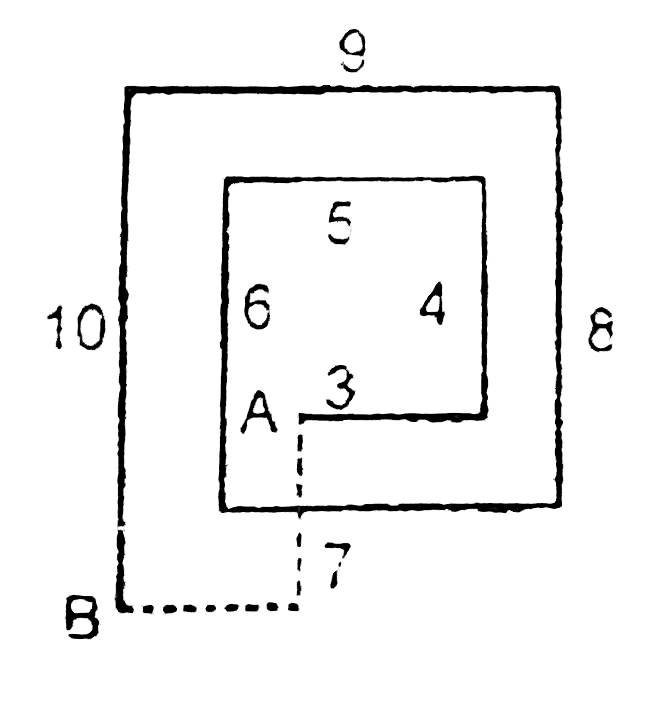 .A2√2mB4√2mC52mDnone of these
.A2√2mB4√2mC52mDnone of theseA particle moves from A to B in a circular path of radius R covering an angle θ as shown in figure. Find the ratio of magnitude of distance and magnitude of displacement of the particle.
 Aθ2.sinθBθ2sin.θ2Cθ2sinθDθsin.θ2
Aθ2.sinθBθ2sin.θ2Cθ2sinθDθsin.θ2
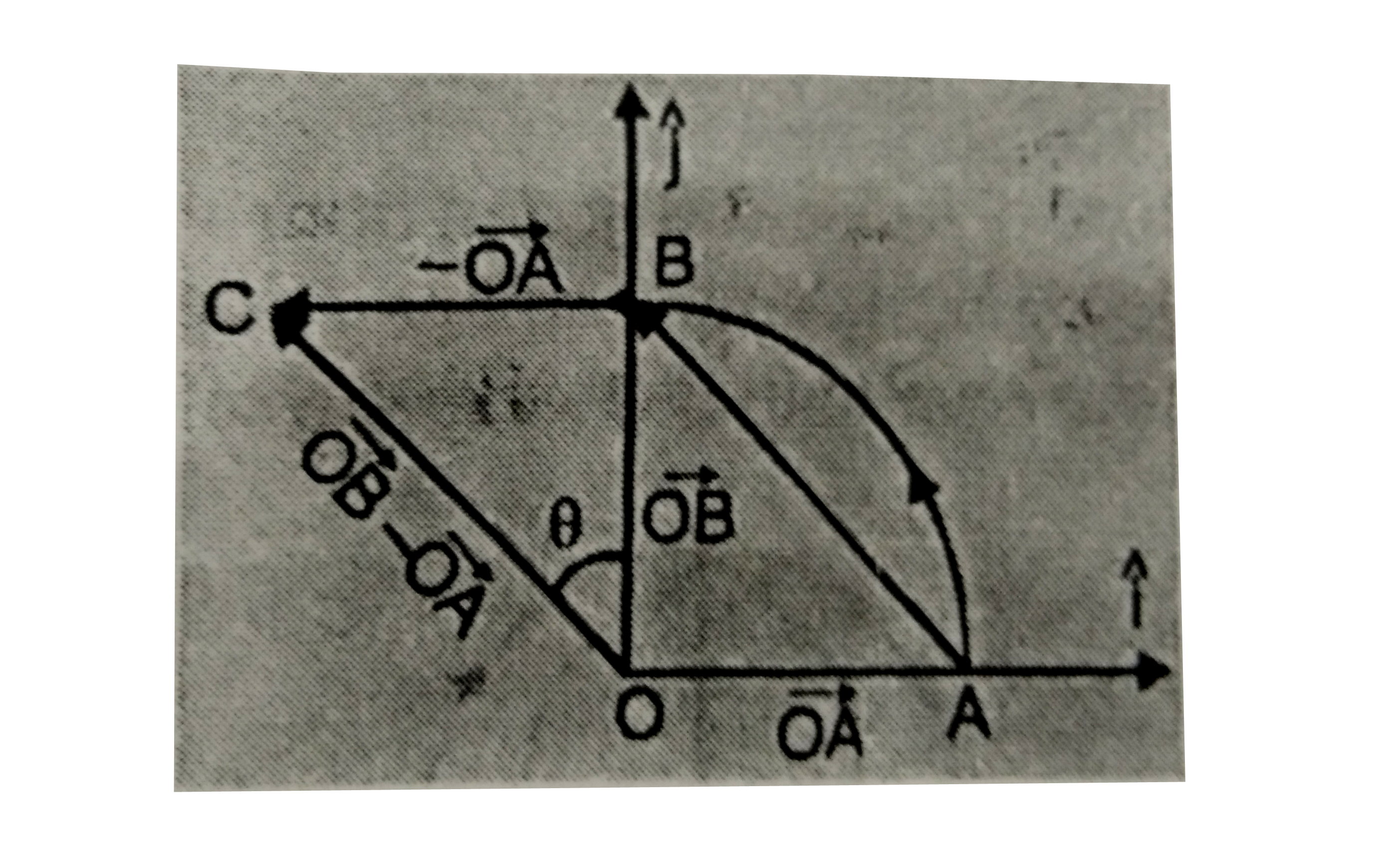
An object moves from position (3,4) to (6,5) in the xy-plane. Find the magnitude and direction of displacement vector of the particle.
View SolutionA particle is moving along a circular path with a constant speed 10ms−1.What is the magnitude of the change in velocity of the particle ,when it moves through an angle of 60∘ around the center of the circle ?
View SolutionA car moves from O to D along the path OABCD shown in fig.
What is distance travelled and net displacement.
View SolutionA particle moves in x−y plane, starting from A along straight line path AB and BC as shown in the graph. When it is at point P, the angle between directions of its average velocity and instantaneous velocity is [tan37∘=3/4]

View SolutionThe velocity - time graph of a particle moving along a straight line is shown in the figure given below
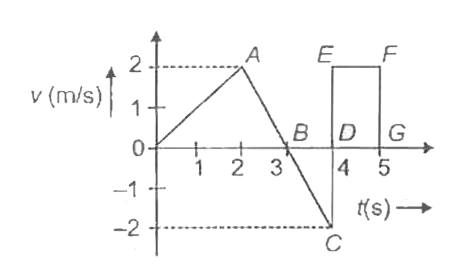
The displacement of the particle in 5 second is
View Solution