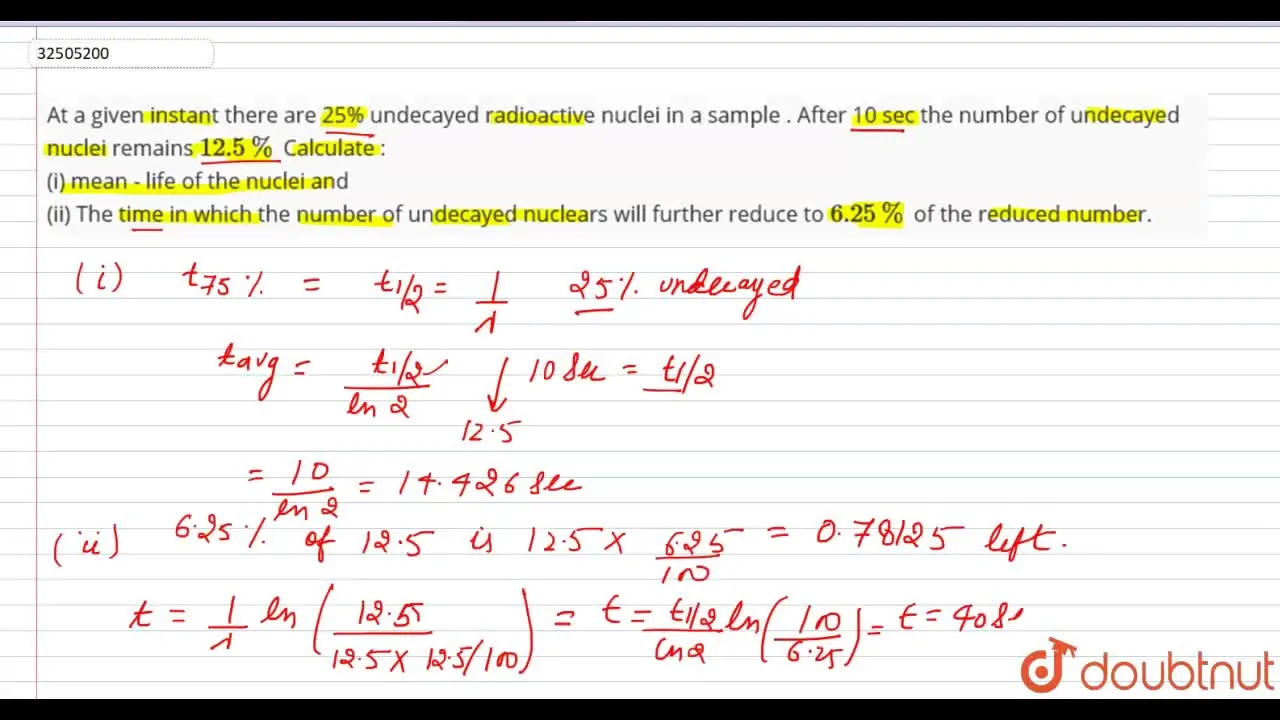
At a given instant there are 25% undecayed radioactive nuclei in a sample . After 10 sec the number of undecayed nuclei remains 12.5 % Calculate :
(i) mean - life of the nuclei and
(ii) The time in which the number of undecayed nuclears will further reduce to 6.25 % of the reduced number.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is: t a v g = 14.43 s (ii) 40 second

( i ) t 75 % =
t 1 / 2 = 1 λ 25% undecayed
t avg = t 1 / 2 ln 2 ↓ 10 sec = t 1 / 2
12.5 % unchecayed
= 10 sec ln 2 = 14.426 sec
(ii) 6.25 % of 12.5 is 12.5 × 6.25 100 = 0.78125 left
t = 1 λ ln ( 12.5 12.5 × 12.5 100 ) ⇒ t = t 1 / 2 ln 2 ln ( 100 6.25 ) ⇒ t = 40 sec

Updated on:21/07/2023
|
Class 12CHEMISTRYCHEMICAL KINETICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • At a given instant, there are 25% undecayed radioactive nuclei in a sample. After 10 seconds the number of undecayed nuclei reduces to 12.5%, the mean life of the nuclei is

    A10.21 s
    B14.43 s
    C5.31 s
    D7.43 s

  • At a given instant there are 25% undecayed radioactive nuclei in a same. After 10sec the number of undecayed nuclei reduces to 6.25%, the mean life of the nuclei is.

    A14.43 sec
    B7.21 sec
    C5 sec
    D10 sec

  • At a given instant, 60% of the radioactive nuclei in a sample are left undecayed. After 20 s, 85% nuclei have disintegrated , mean life of nuclei

    A10 s
    B6.93 s
    C14.43 s
    D12.86 s