A block moving with strikes a spring of constant attached to block at rest kept on a smooth floor. The time for which rear moving block remain in contact with spring will be-
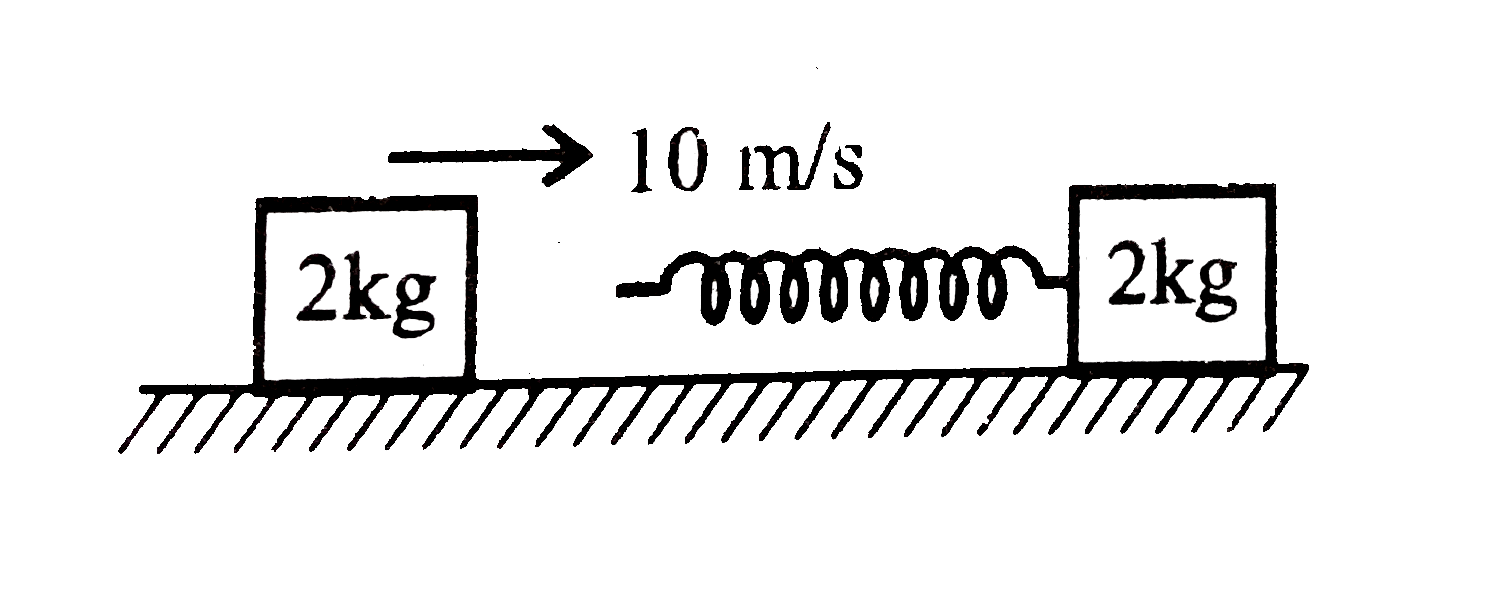
The correct Answer is:A
_E01_085_S01.png)
Let velocity of rear be and front be then
Now by conservation of mechanical energy
But
as
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (4)
2 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (5)
3 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (2)
2 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
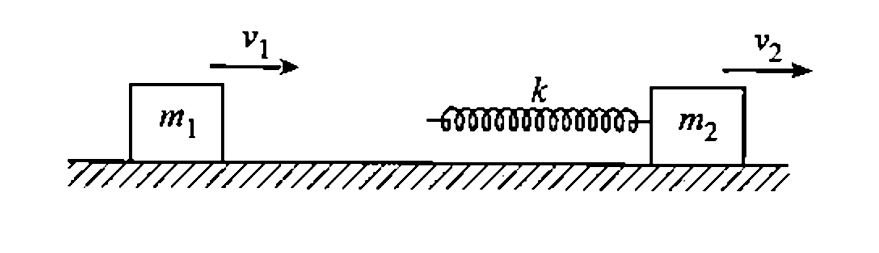
A block of mass m1 =2 kg slides along a firictionless table with a speed of 10m/s. Directly infront of it,and moving in the same direction is a block of mass m2 5 kg moving at 3 m/s. A mass less spring with a spring constant 11.2 N/cm is attached to as shown in figure-5.146. When the block collide,what is the maximum compression of the spring ? Assume that the spring does not bend.
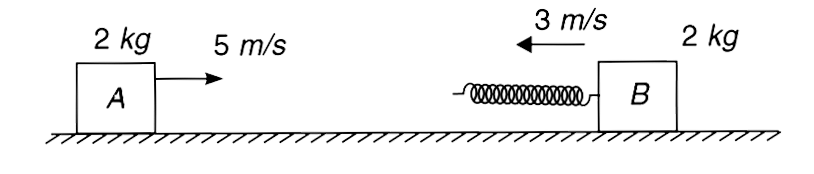
View SolutionA block A of mass 2kg is moving to right with a speed of 5 m/s on a horizontal smooth surface. Another block B of mass 2 kg, with a mass less spring of force constant K=200 N/m attached to it, is moving to left on the same surface with a speed of 3 m/s. Block A collides with the spring attached to B. Calculate
(a) the final velocity of the block A.
(b) the minimum kinetic energy of the system of two blocks during subsequent motion.
(c) Repeat part (b) if there is no spring and the two blocks collide head on. Assume that the blocks are made of perfectly elastic material
View Solution
Knowledge Check
Two springs of spring constant 6N/m and 4N/m are attached to a block of mass 1 kg and to fixed support. Then time period of the given oscillation is
(consider √10=π)A1sB2sC0.5sD4sA bullet weighing 10 g and moving with a velocity 300 m/s strikes a 5 kg block of ice and drop dead. The ice block is kept on smooth surface. The speed of the block after the the collision is
A6 cm/sB60 cm/sC6 m/sD0.6 cm/sA block of mass 'm' is connected to another block of mass 'M' by a spring (massless) of spring constant 'k' The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched Then a constant force 'F' starts acting on the block of mass 'M' to pull it. Find the force on the block of mass 'm' :
AMF(m+M)BmFMC(M+m)FmDmF(m+M)
A block of mass m is connect to another block of mass M by a massless spring of spring constant k. The blocks are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unsrtretched when a constnt force F starts acting on the block of mass M to pull it. Find the maximum extension of the spring.

View SolutionA block of mass 0.18kg is attached to a spring of force-constant 2N/m. The coefficient of friction between the block and the floor is 0.1 Initially the block is at rest and the spring is un-stretched. An impulse is given to the block as shown in the figure. The block slides a distance of 0.06m and comes to rest for the first time. The initial velocity of the block in m//s is V=N/10. Then N is :
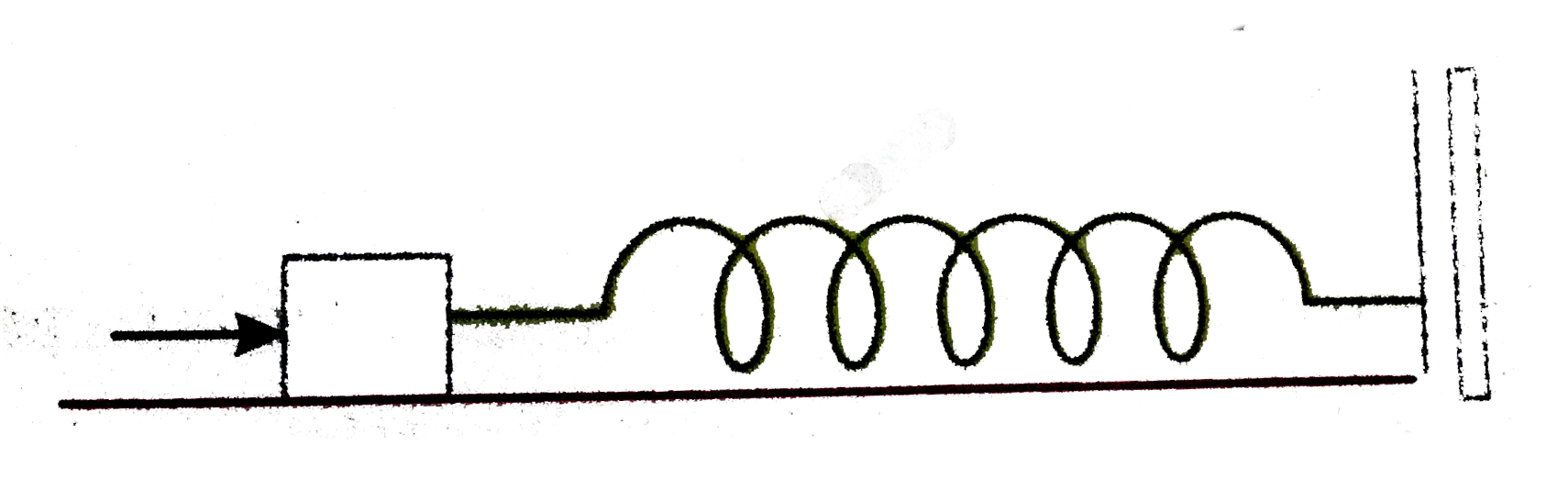 .
.
View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural length
View Solution
