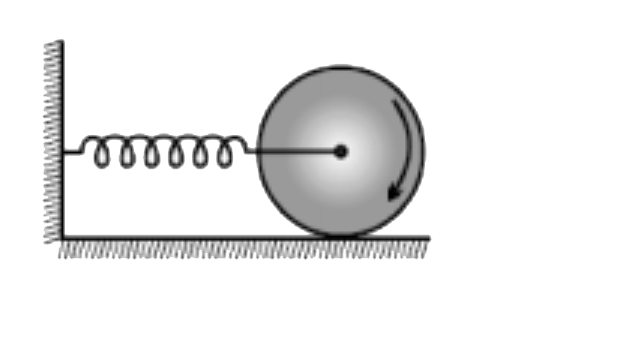
Passage VIII A disc of mass m and radius R is attached with a spring of force contant k at its center as shown in figure. At x-0, spring is unstretched. The disc is moved to x=A and then released. There is no slipping between disc and ground. Let f be the force of friction on the disc from the ground.

f versus t (time) graph will be as
_E01_082_O01.png)
_E01_082_O02.png)
_E01_082_O03.png)
_E01_082_O04.png)
The correct Answer is:C
_E01_082_S01.png)
kx−f=ma,fR=(mR22)α=f=13kx
But x=Acosωt
(∴ the cylinder is starting from x=A)
So f=kA3cosωt
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Comprehension Base Questions (3)
Explore 2 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Comprehension Base Questions (4)
Explore 2 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Comprehension Base Questions (1)
Explore 2 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
A uniform disc of mass M and radius R is hinged at its centre C . A force F is applied on the disc as shown . At this instant , angular acceleration of the disc is

View SolutionA disc of mass M and radius R moves in the x-y plane as shown in the figure. The angular momentum of the disc at the instant shown is –
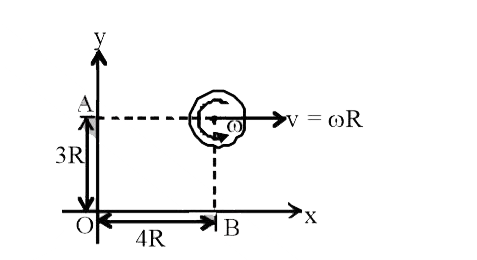
View Solution
Knowledge Check
A uniform disc of mass m & radius R is pivoted at its centre O with its plane vertical as shown in figure A circular portion of disc of radius R2 is removed from it. Then choose the correct option(s)
 ATime period of small oscillations of remaining portion about O is π√13RgBTime period of small oscillations of remaining portion about O is 2π√13RgCThe centre of mass of the remaining disc is at a distance of R6 from O.DThe centre of mass of the remaining disc is at a distance of R8 from O.
ATime period of small oscillations of remaining portion about O is π√13RgBTime period of small oscillations of remaining portion about O is 2π√13RgCThe centre of mass of the remaining disc is at a distance of R6 from O.DThe centre of mass of the remaining disc is at a distance of R8 from O.A disc of mass M is attached to a horizontal massless spring of force constant K so that it can roll with out slipping along a horizontal surface. If the disc is pulled a little towards right and then released, its centre of mass executes SHM with a period of
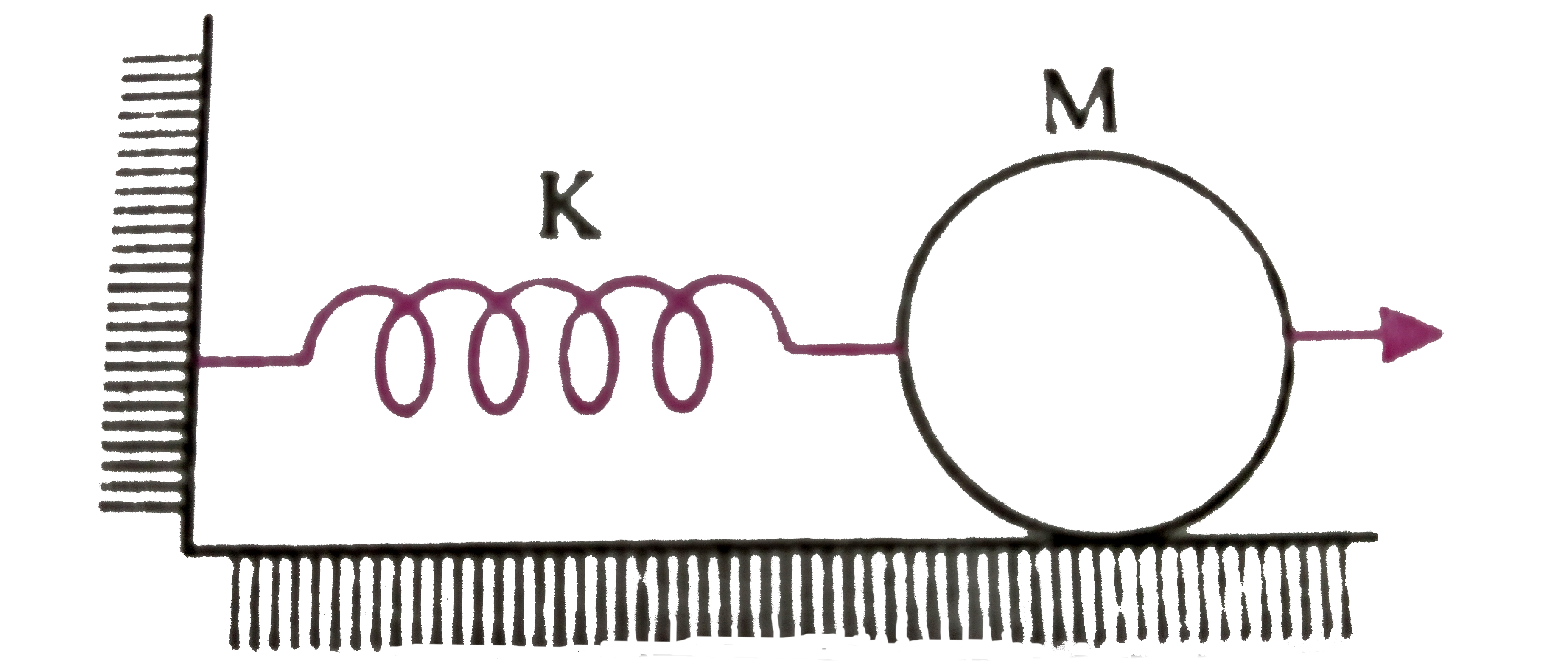 A2π√MKB2π√3MKC2π√M2KD2π√3M2K
A2π√MKB2π√3MKC2π√M2KD2π√3M2KA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank isAF2BF4CF3D2F3
A uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:

View SolutionA uniform disc of mass M and radius R is hinged at its centre C. A force F is applied on the disc as shown. At this instant, the angular acceleration of the disc is
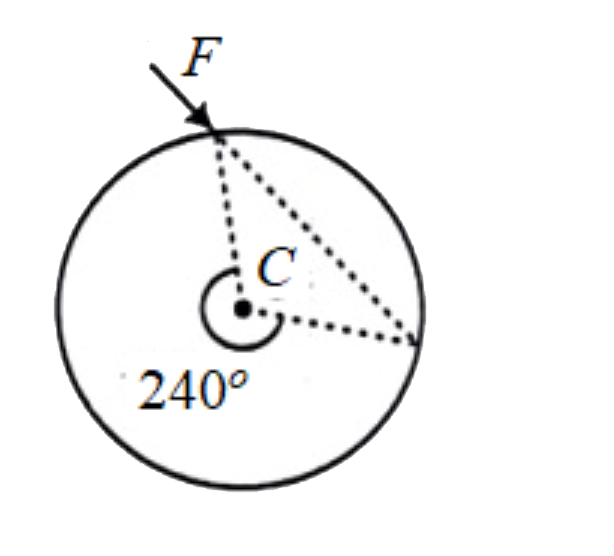
View SolutionA thin disc of mass 9M and radius R from which a disc of radius R/3 is cut shown in figure. Then moment of inertia of the remaining disc about O, perpendicular to the plane of disc is -
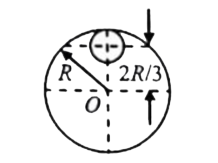
View SolutionA disc of mass M and radius R rolls on a horizontal surface and then rolls up an inclined plane as shown in the figure. If the velocity of the disc is v, the height to which the disc will rise will be:

View SolutionA disc of mass M and radius R has a spring of constant k attached to its center , the other end of the spring being fixed to a vertical wall. If the disk rolls without slipping on a level floor, how far to the right does the centre of mass move , if Initially the spring was unstretched and the angular speed of the disc was ω0
View Solution

