A cylindrical block of the density ρ is partically immersed in a liwuid of density 3ρ. The plane surface of the block remains parallel to the surface of the liquid. The height of the block is 60m. The block perform SHM when displaced form its mean position [Use g=9.8m/s2]
the maximum amplitude is 20cm.
the maximum amplitude is 40cm
the time period will be 2π/7 seconds
none
The correct Answer is:A, C
To solve the problem step by step, we will analyze the situation involving the cylindrical block and the liquid.
Step 1: Understand the System
We have a cylindrical block of density ρ partially immersed in a liquid of density 3ρ. The height of the block is 60cm (or 0.6m). The block performs simple harmonic motion (SHM) when displaced from its mean position.
Step 2: Determine the Equilibrium Condition
At equilibrium, the buoyant force acting on the block equals the weight of the block. The buoyant force Fb can be expressed as:
Fb=density of liquid×volume of liquid displaced×g
The volume of liquid displaced when the block is partially submerged to a height y is:
Volume displaced=A⋅y
where A is the cross-sectional area of the block.
Thus, the buoyant force becomes:
Fb=3ρ⋅(A⋅y)⋅g
The weight of the block W is:
W=density of block×volume of block×g=ρ⋅(A⋅0.6)⋅g
Setting the buoyant force equal to the weight of the block gives us:
3ρ⋅(A⋅y)⋅g=ρ⋅(A⋅0.6)⋅g
Step 3: Simplify the Equation
We can cancel A and g from both sides:
3y=0.6
Solving for y:
y=0.63=0.2m=20cm
Step 4: Determine the Amplitude of SHM
The amplitude of the SHM is the maximum displacement from the equilibrium position. Since the block is initially at equilibrium with y=20cm, this is the amplitude of the motion.
Step 5: Calculate the Time Period of SHM
The effective spring constant k for the system can be derived from the buoyant force. The restoring force when the block is displaced by a small distance x from its equilibrium position is:
F=−ΔV⋅density of liquid⋅g=−3ρA(y+x)g+3ρAyg
This simplifies to:
F=−3ρAg⋅x
Thus, k=3ρAg.
The mass m of the block is:
m=ρ⋅(A⋅0.6)
Using the formula for the time period T of SHM:
T=2π√mk=2π√ρ⋅(A⋅0.6)3ρAg=2π√0.63g
Step 6: Substitute Values
Substituting g=9.8m/s2:
T=2π√0.63⋅9.8=2π√0.629.4=2π√0.0204
Calculating T:
T≈2π⋅0.142=0.891s≈2π/7s
Final Results
- The maximum amplitude of the SHM is 20cm.
- The time period of the SHM is approximately 2π7s.
We have a cylindrical block of density ρ partially immersed in a liquid of density 3ρ. The height of the block is 60cm (or 0.6m). The block performs simple harmonic motion (SHM) when displaced from its mean position.
At equilibrium, the buoyant force acting on the block equals the weight of the block. The buoyant force Fb can be expressed as:
Fb=density of liquid×volume of liquid displaced×g
The volume of liquid displaced when the block is partially submerged to a height y is:
Volume displaced=A⋅y
where A is the cross-sectional area of the block.
Fb=3ρ⋅(A⋅y)⋅g
W=density of block×volume of block×g=ρ⋅(A⋅0.6)⋅g
3ρ⋅(A⋅y)⋅g=ρ⋅(A⋅0.6)⋅g
We can cancel A and g from both sides:
3y=0.6
Solving for y:
y=0.63=0.2m=20cm
The amplitude of the SHM is the maximum displacement from the equilibrium position. Since the block is initially at equilibrium with y=20cm, this is the amplitude of the motion.
The effective spring constant k for the system can be derived from the buoyant force. The restoring force when the block is displaced by a small distance x from its equilibrium position is:
F=−ΔV⋅density of liquid⋅g=−3ρA(y+x)g+3ρAyg
This simplifies to:
F=−3ρAg⋅x
Thus, k=3ρAg.
m=ρ⋅(A⋅0.6)
T=2π√mk=2π√ρ⋅(A⋅0.6)3ρAg=2π√0.63g
Substituting g=9.8m/s2:
T=2π√0.63⋅9.8=2π√0.629.4=2π√0.0204
Calculating T:
T≈2π⋅0.142=0.891s≈2π/7s
- The maximum amplitude of the SHM is 20cm.
- The time period of the SHM is approximately 2π7s.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise- 3 Match The Column
Explore 1 Video
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Asseration & Reason
Explore 7 Videos
- SIMPLE HARMONIC MOTIONBook:ALLENChapter:SIMPLE HARMONIC MOTIONExercise:Exercise-01
Explore 117 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 25 Videos
- TEST PAPERBook:ALLENChapter:TEST PAPERExercise:PHYSICS
Explore 4 Videos
Similar Questions
In Fig. , a rectangular block floats in a liquid . A block of mass m = 0.500 kg and density ρ=700kg/m3 floats face down in a liquid of density ρf=1200kg/m3 . What are the magnitude of the buoyant force on the block from the liquid , the weight of the liquid displaced by the block (liquid that would be in the space now occupied by the block ) , and the mass of that displaced liquid ? What fraction of the block's volume is submerged ? What fraction of its height is submerged ?

View SolutionA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View Solution
Knowledge Check
A triangular lamina of area A and height h is immersed in a liquid of density ρ in a vertical plane with its base on the surface of the liquid. The thrust on the lamina is.
A12AρghB13AρghC16AρghD23AρghA ball of mass m and density ρ is immersed in a liquid of density 3ρ at a depth h and released. To what height will the ball jump up above the surface of liqud ? (neglect the reistance of water and air).
AhBh/2C2hD3hAn open pan P filled with water (density ρm) is placed on one side of the pan as shown. If water depth is more then height of the block, then choose the correct statement.
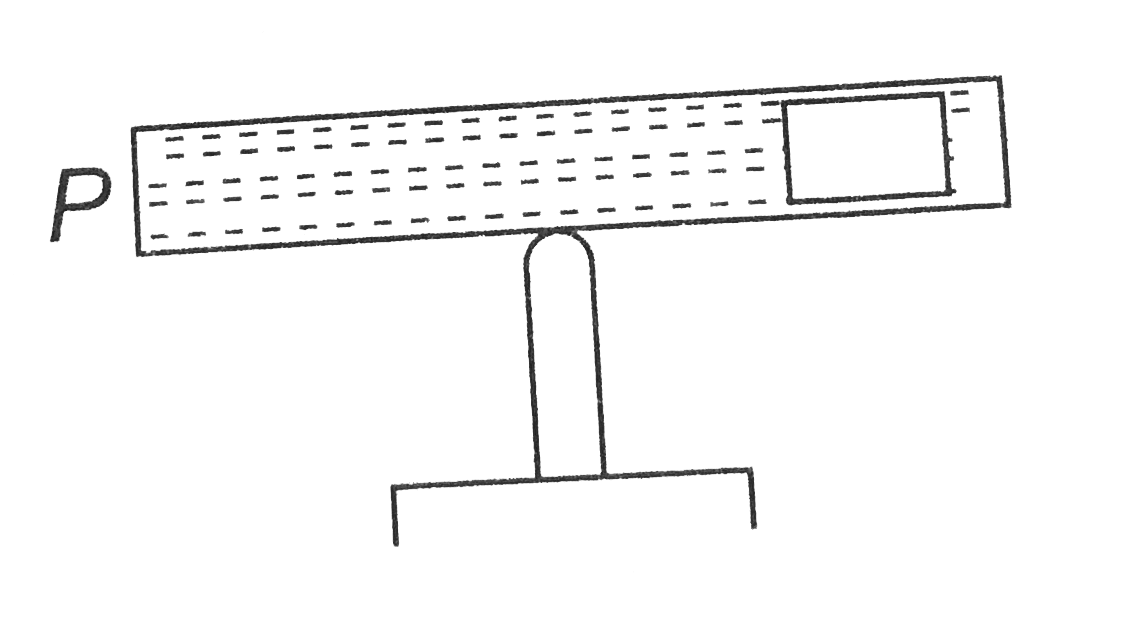 AEquilibrium will be maintained only if ρ<ρw.BEquilibrium will be maintained only ρ≤ρw.CEquilibrium will be maintained for all relation between ρandρw.DEquilibrium will not be maintained in all cases.
AEquilibrium will be maintained only if ρ<ρw.BEquilibrium will be maintained only ρ≤ρw.CEquilibrium will be maintained for all relation between ρandρw.DEquilibrium will not be maintained in all cases.
A block of volume V and density ρ is floating in a liquid of density 2ρ filled in a vessel. Now the vesset starts falling freely with acceleration g. Then the volume of block inside the liquid in the falling condition is
View Solution
Cylindrical block of area of cross-section A and of material of density ρ is placed in a liquid of density one third of density of block. The block compress in the spring is one-third of te length of the block. if acceleration due to gravity is g, the spring constant of the spring is
View SolutionA block of mass 5 kg and volume 0.05m3 floats in a liquid of density 140kg m−3 .
Volume of block above the surface of liquid is
View SolutionA cubical block of wood of edge a and density ρ floats in water of density 2ρ. The lower surface of the cube just touches the free end of a mass less spring of force constant K fixed at the bottom of the vessel. The weight W put over the block so that it is completely immersed in water without wetting the weight is
View SolutionA small block of wood of relative density 0.5 is submerged in water at a depth of 5 m When the block is released it starts moving upwards, the acceleration of the block is (g=10ms−2)
View Solution

