A block of volume V and density ρ is floating in a liquid of density 2ρ filled in a vessel. Now the vesset starts falling freely with acceleration g. Then the volume of block inside the liquid in the falling condition is
V
V/2
arbitray
zero
The correct Answer is:C
To solve the problem, we need to analyze the situation step by step:
Step 1: Understand the Scenario
We have a block of volume V and density ρ floating in a liquid of density 2ρ. The vessel containing the liquid is falling freely with an acceleration equal to g.
Step 2: Identify Forces Acting on the Block
In normal conditions (when the vessel is not falling), the block experiences two main forces:
1. The gravitational force acting downwards: Fg=mg=ρVg
2. The buoyant force acting upwards: Fb=density of liquid×volume of liquid displaced×g=2ρV′g, where V′ is the volume of the block submerged in the liquid.
Step 3: Analyze the Condition of Free Fall
When the vessel is in free fall, both the block and the liquid are accelerating downwards with acceleration g. This means that the effective weight of the block and the buoyant force are both negated by the free fall.
Step 4: Pressure Difference in Free Fall
In free fall, the pressure difference between any two points in the liquid becomes zero because both points are accelerating downwards at the same rate. Therefore, the buoyant force acting on the block becomes zero.
Step 5: Conclusion About the Block's Volume in Liquid
Since the buoyant force is zero, there is no upward force acting on the block. This means that the block can occupy any volume inside the liquid without being pushed upwards. Therefore, the volume of the block submerged in the liquid can be arbitrary.
Final Answer
The volume of the block inside the liquid in the falling condition is arbitrary.
---
We have a block of volume V and density ρ floating in a liquid of density 2ρ. The vessel containing the liquid is falling freely with an acceleration equal to g.
In normal conditions (when the vessel is not falling), the block experiences two main forces:
1. The gravitational force acting downwards: Fg=mg=ρVg
2. The buoyant force acting upwards: Fb=density of liquid×volume of liquid displaced×g=2ρV′g, where V′ is the volume of the block submerged in the liquid.
When the vessel is in free fall, both the block and the liquid are accelerating downwards with acceleration g. This means that the effective weight of the block and the buoyant force are both negated by the free fall.
In free fall, the pressure difference between any two points in the liquid becomes zero because both points are accelerating downwards at the same rate. Therefore, the buoyant force acting on the block becomes zero.
Since the buoyant force is zero, there is no upward force acting on the block. This means that the block can occupy any volume inside the liquid without being pushed upwards. Therefore, the volume of the block submerged in the liquid can be arbitrary.
The volume of the block inside the liquid in the falling condition is arbitrary.
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Integer type q.
15 Videos
Similar Questions
A solid of density σ floats in a liquid of density ρ. What will happen to level of liquid if solid melts ?
View SolutionA small ball of volume V and density ρ is held inside a cubical container of side L filled with an ideal liquid of density 4ρ as .Now if the container started moving with constant acceleration a and the ball it hits the top corner point Q of the container . Then find the value of k . Given g=10m/s2
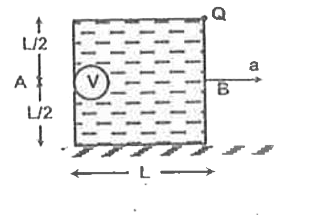
View Solution
Knowledge Check
A body of volume V and density d is completely immersed in a liquid of density p. Then the apparent weight of the body will be:
AVdgBVρgCV(ρ−d)gDV(d−ρ)gA ball of density ρ is released from deep inside of a liquid of density 2ρ. It will move up
Awith an increasing accelerationBwith a decreasing accelerationCwith a constant accelerationDwith zero accelerationWhen a body of density d1 and volume V is floating in a liquid of density d2
Aits true weight is Vd2gBloss in its weight is Vd2gCits apparent weight is zeroDits density d1 is greater than that of liquid d2 .
A ball of volume V and density ρ1 is moved downwards by a distance 'd' in liquid of density ρ2. Find total change in potential energy of the system.

View SolutionA body floats in a liquid contained in a vessel. The vessel falls vertically with an acceleration ( a (< g). If Vi and Vf be the initial and final volume of the body immersed in the liquid then :
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If ρ is the surface tension the diameter of the drop of the liquid is
View SolutionA drop of liquid of density ρ is floating half-immersed in a liquid of density d. If ρ is the surface tension the diameter of the drop of the liquid is
View SolutionA block of density ρ floats in a liquid with its one third volume immersed. The density of the liquid is
View Solution