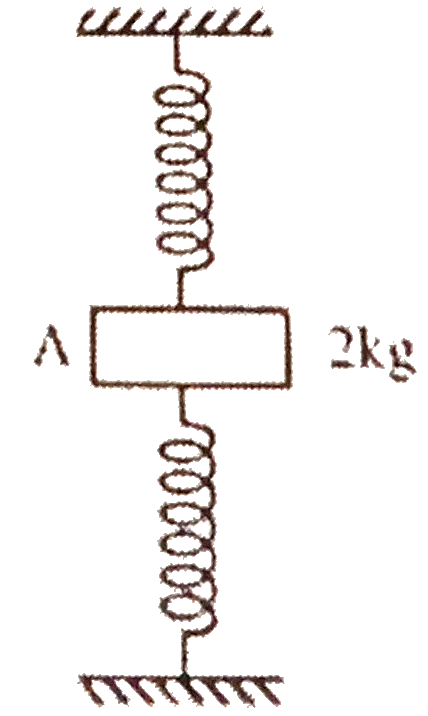
Block A in the figure is released from the rest when the extension in the spring is x0. The maximum downward displacement of the block will be :
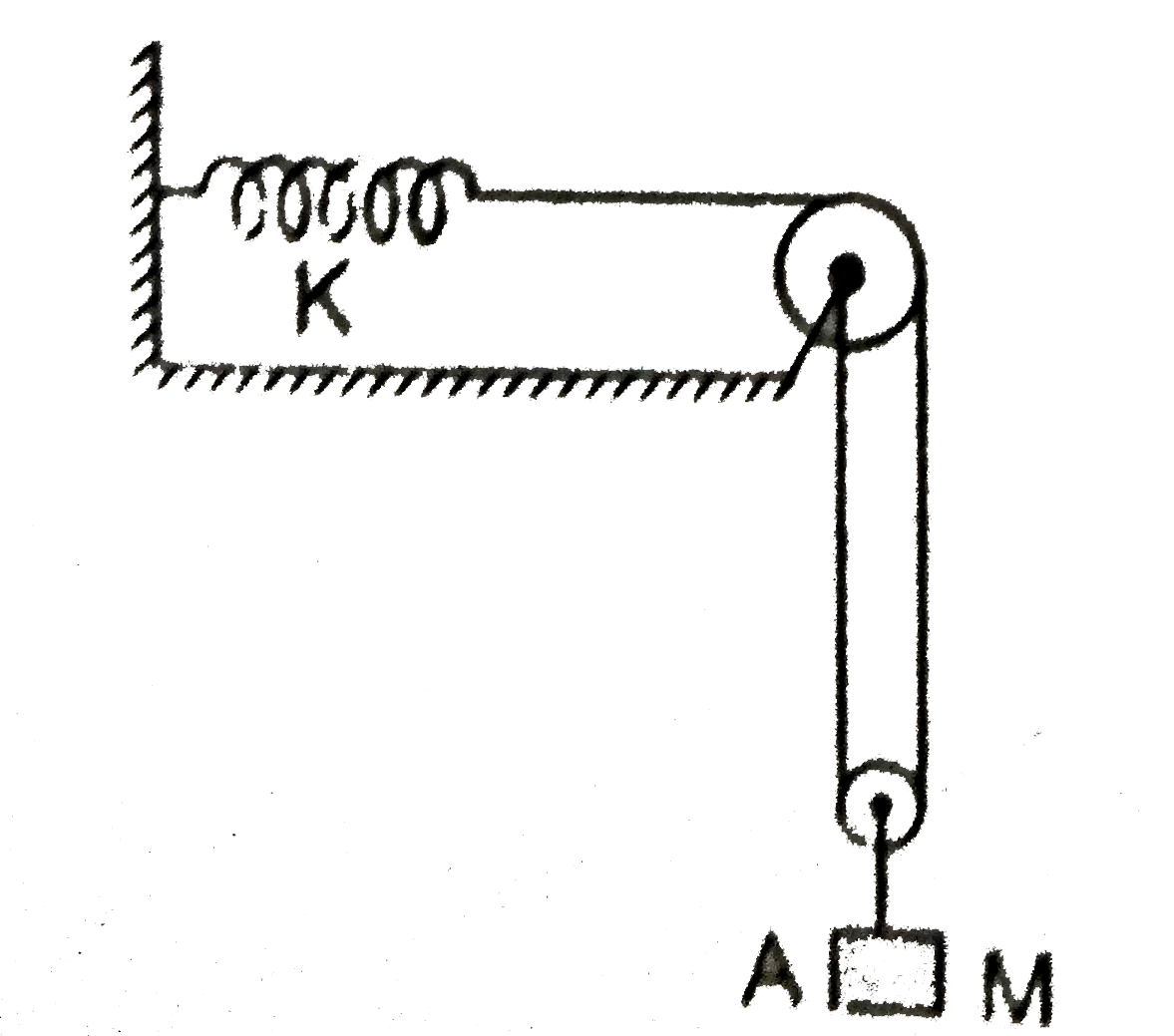
Mg2k−x0
Mg2k+x0
2Mgk−x0
2Mgk+x0
The correct Answer is:A
For maximum displacement
Mg(x)=12k(2x)2⇒x=Mg2k⇒x=mg2k−x0
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-02
19 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise- 3 Match The Column
1 Video
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Video
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
In figure, the stiffness of the spring is k and mass of the block is m. The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block m. Neglect the mass of the spring and that of the string. Also neglect the friction.
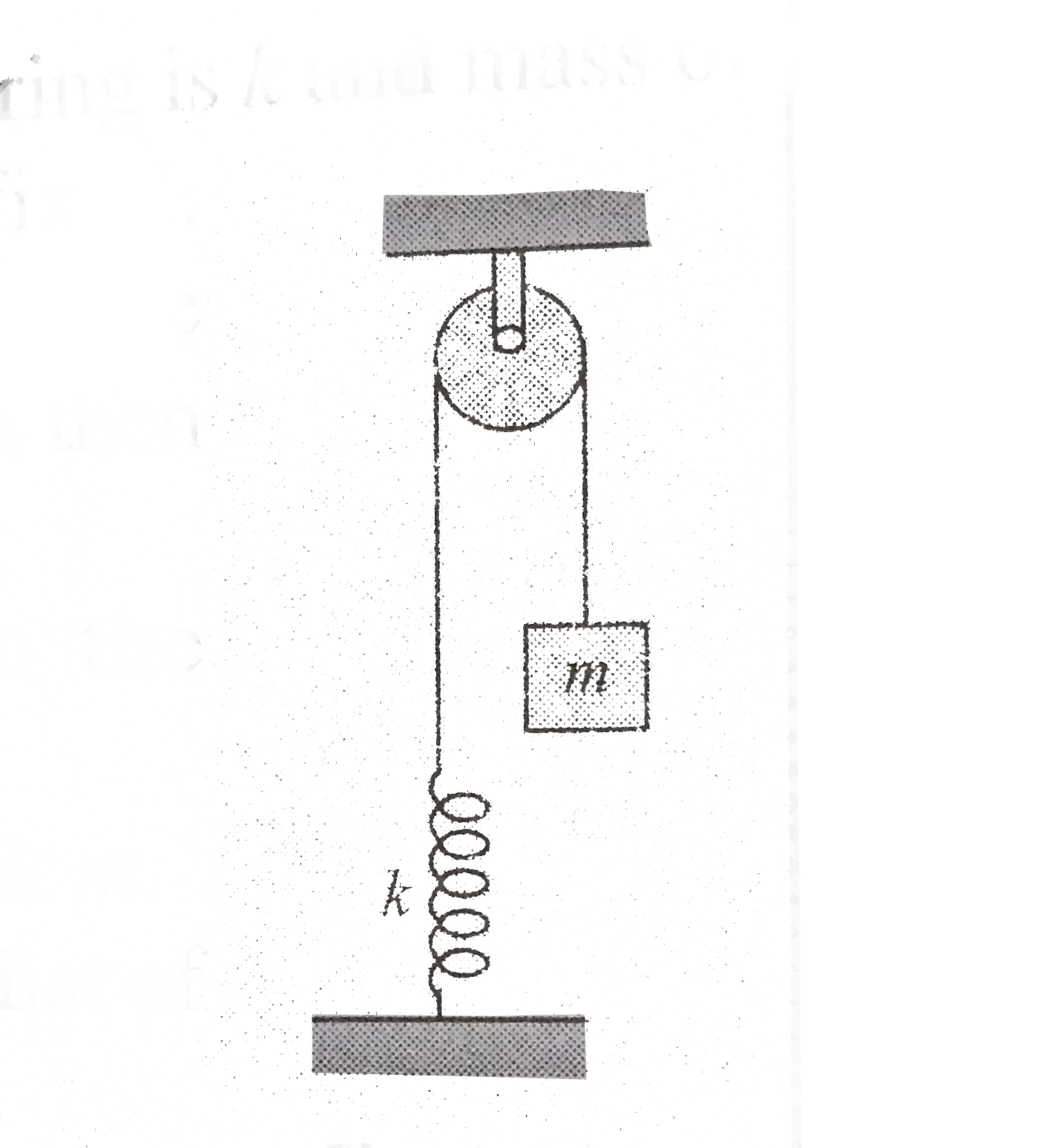
View SolutionIn the system shown in figure, the block A is released from rest. Find
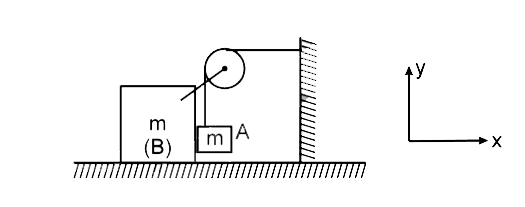
Tension in the string.
View Solution
Knowledge Check
Block A in the figure is released from rest when the extension in the spring is x0(x0<mg/k). The maximum downward displacement of the block is (there is no friction) :
 A2MgK−2x0BMg2K+x0C2MgK−x0D2MgK+x0
A2MgK−2x0BMg2K+x0C2MgK−x0D2MgK+x0Block A of the mass M in the figure is released from rest when the extension in the spring is x0. The maximum downwards displacement of the block is (assume x0<Mg/k).
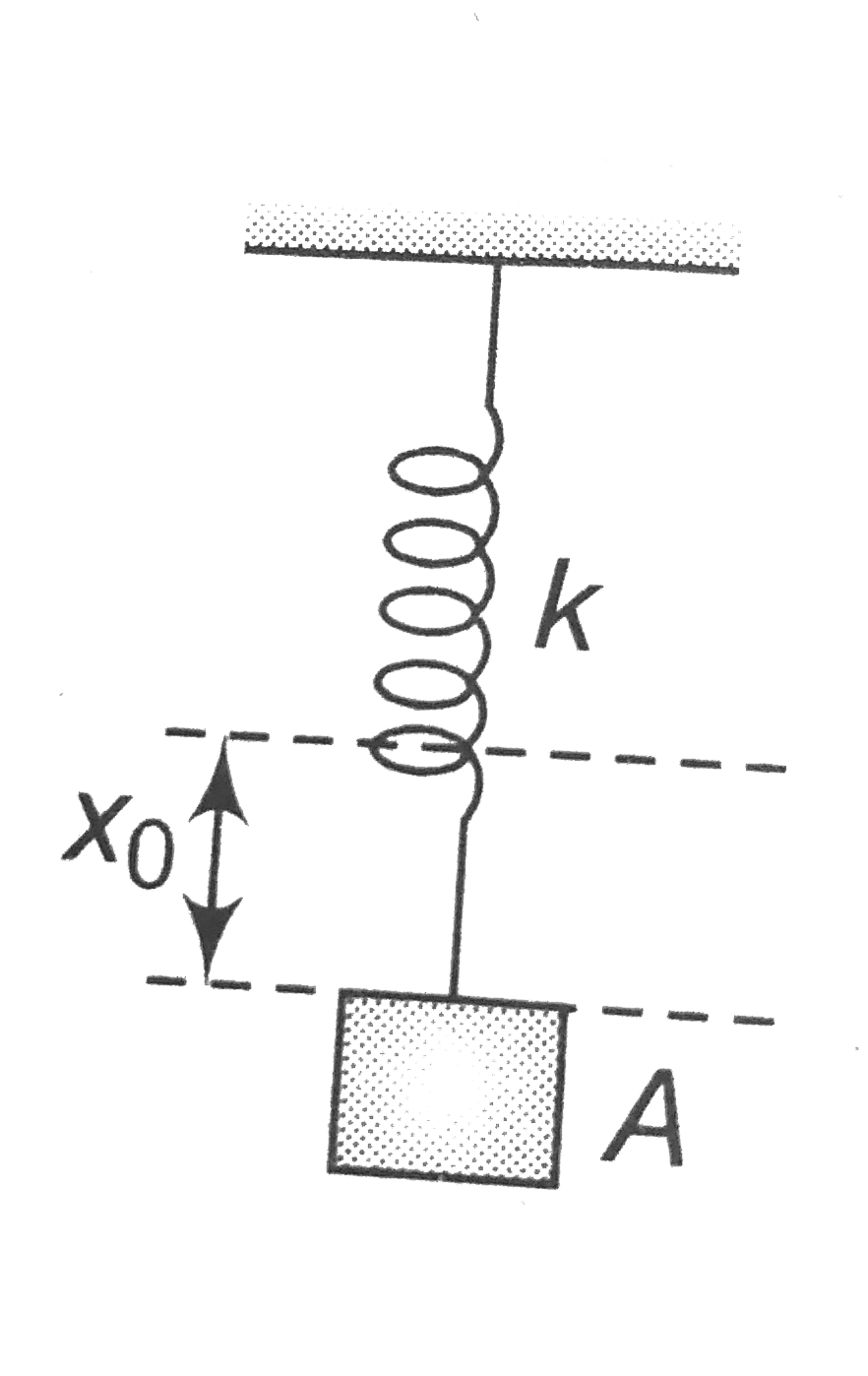 A2(Mgk−x0)BMg2k+x0C2Mgk−x0D2Mgk+x0
A2(Mgk−x0)BMg2k+x0C2Mgk−x0D2Mgk+x0In above question, speed of block A, when the extension in spring is xm2, is:
A2g√mkB2g√2mkC2g√2m3kDg√4m3k
The block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m

View SolutionTwo blocks each of mass m, connected by an un-stretched spring are kept at rest on a frictionless horizontal surface. A constant force F is applied on one of the blocks pulling it away from the other as shown in figure.
 (a)Find accelaration of the mass center.
(a)Find accelaration of the mass center.
(b) Find the displacement of the centre of mass as function of time t.
(c) If the extension of the spring is X0 at an instant t, find the displacements of the two blocks relative to the ground at this instant.
View SolutionA block A of mass 2 kg is connected with two springs, as shown . The spring constant of lower spring is system is thrice the spring costant of upper spring. The system is released from rest with both the springs unstreched. The maximum displacement of bloack is 0.1m. Find the acceleration of the block is its lowest position-
View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the first block at this instant is
View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the second block at this instant is
View Solution
