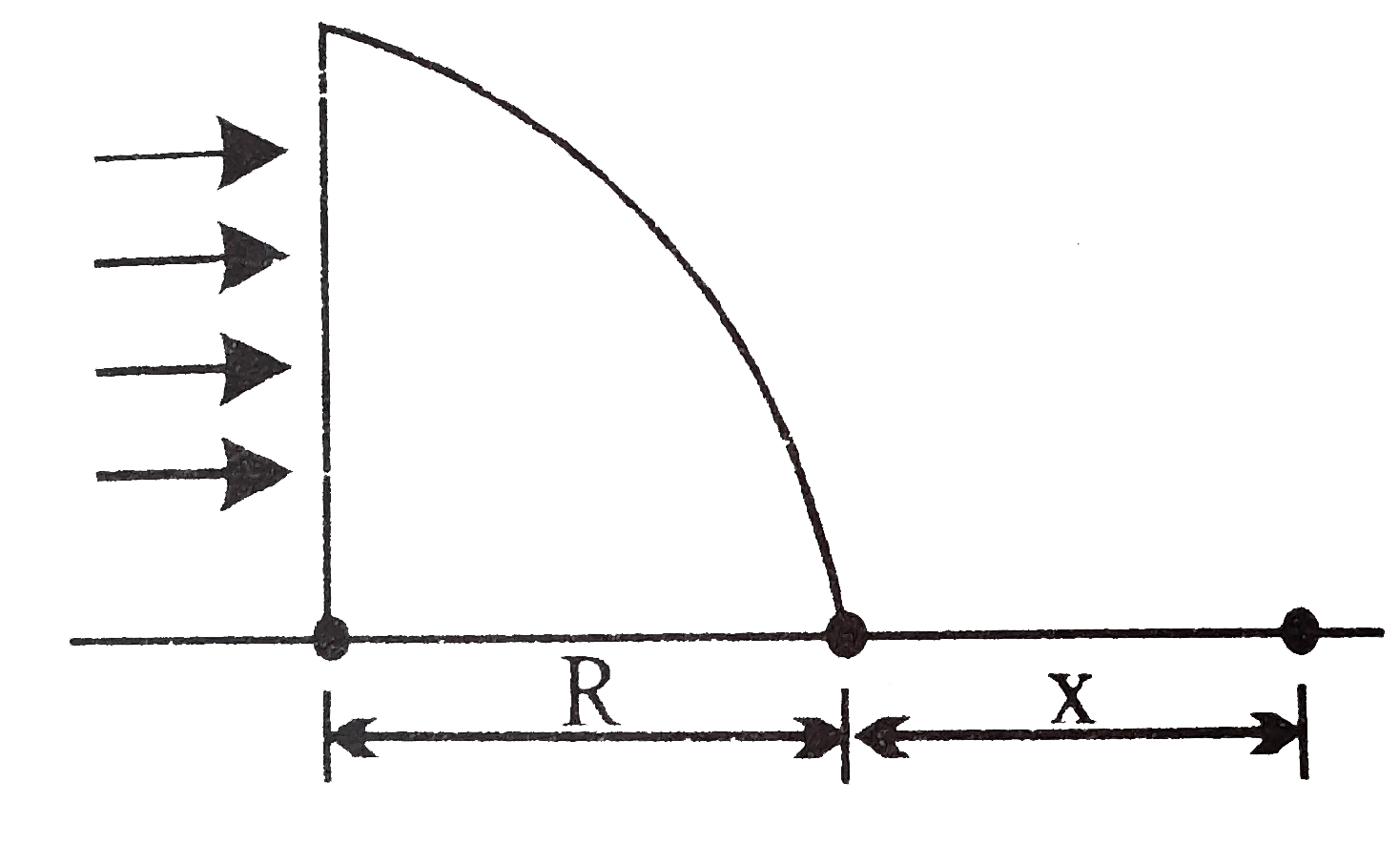
A uniform,horizontal beam of light is incident upon a quarter cylinder of radiusR=5cm and has a refractive index 2/√3.A patch on the table for a distance 'x'from the cylinder is unilluminated ,find the value of 'x'?
The correct Answer is:5 m
_E01_152_S01.png)
Sin C = 1μ = (1)/(2//sqrt(3))<br>implies C = Sin^(-1) (sqrt(3))/(2) = 60^(@)<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_C07(II)_E01_152_S02.pngwh=80%mx-autosty≤=background:white;><br>"cos"60^(@) = (R)/(R+x) implies x = R , x = 5 cm
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-05 (A)
35 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-05 (B)
35 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[A]
23 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A uniform, horizontal parallel beam of light is incident upon a prism as shown. The prism is in the shape of a quarter cylinder, of radius 5cm, and has refractive index 5/3. The width of the regionat which the incident rays after normal incidence on plane surface and subsequent refraction at curved surface intersect on x axis is (Neglect the ray which travels along x-axis)
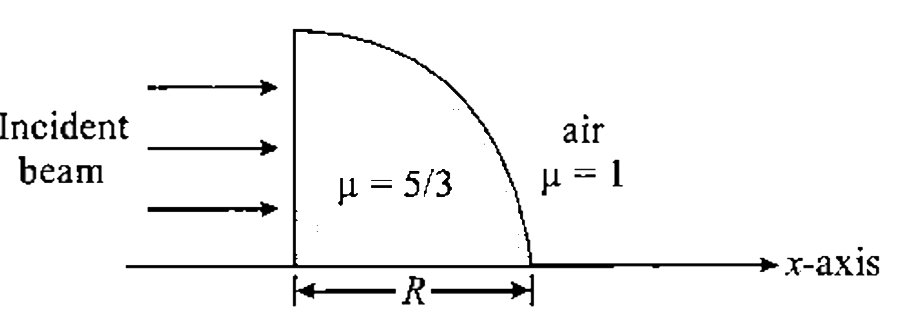
View SolutionA horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
View Solution
Knowledge Check
A parallel beam of light is incident normally on the flat surface of a hemisphere of radius 6cm and refractive index 1.5, placed in air as shown in figure (i). Assume paraxial ray approxiamtion.
 .AThe rays are focused at 12cm from the point P to the right, in the solutation as shown in figure (i)BThe rays are focused at 16cm from the point P to the right, in the situation as shown in figure (i).CIf the rays are incident at the curved surface (figure (ii)) then these are focused at distance 18cm from point P to the rightDIf the ray are incident at the curved surface (figure(ii)) then these are focused at distance 14cm from point P to the right.
.AThe rays are focused at 12cm from the point P to the right, in the solutation as shown in figure (i)BThe rays are focused at 16cm from the point P to the right, in the situation as shown in figure (i).CIf the rays are incident at the curved surface (figure (ii)) then these are focused at distance 18cm from point P to the rightDIf the ray are incident at the curved surface (figure(ii)) then these are focused at distance 14cm from point P to the right.As shown, a narrow beam of light is incident onto a semi-circular glass cylinder of radius R. Light can exit the cylinder when the beam is at the centre. When the beam is moved parallel to a maximum distance d from the central line, no light can exit the cylinder from its lower surface. Find the refractive index of the glass.
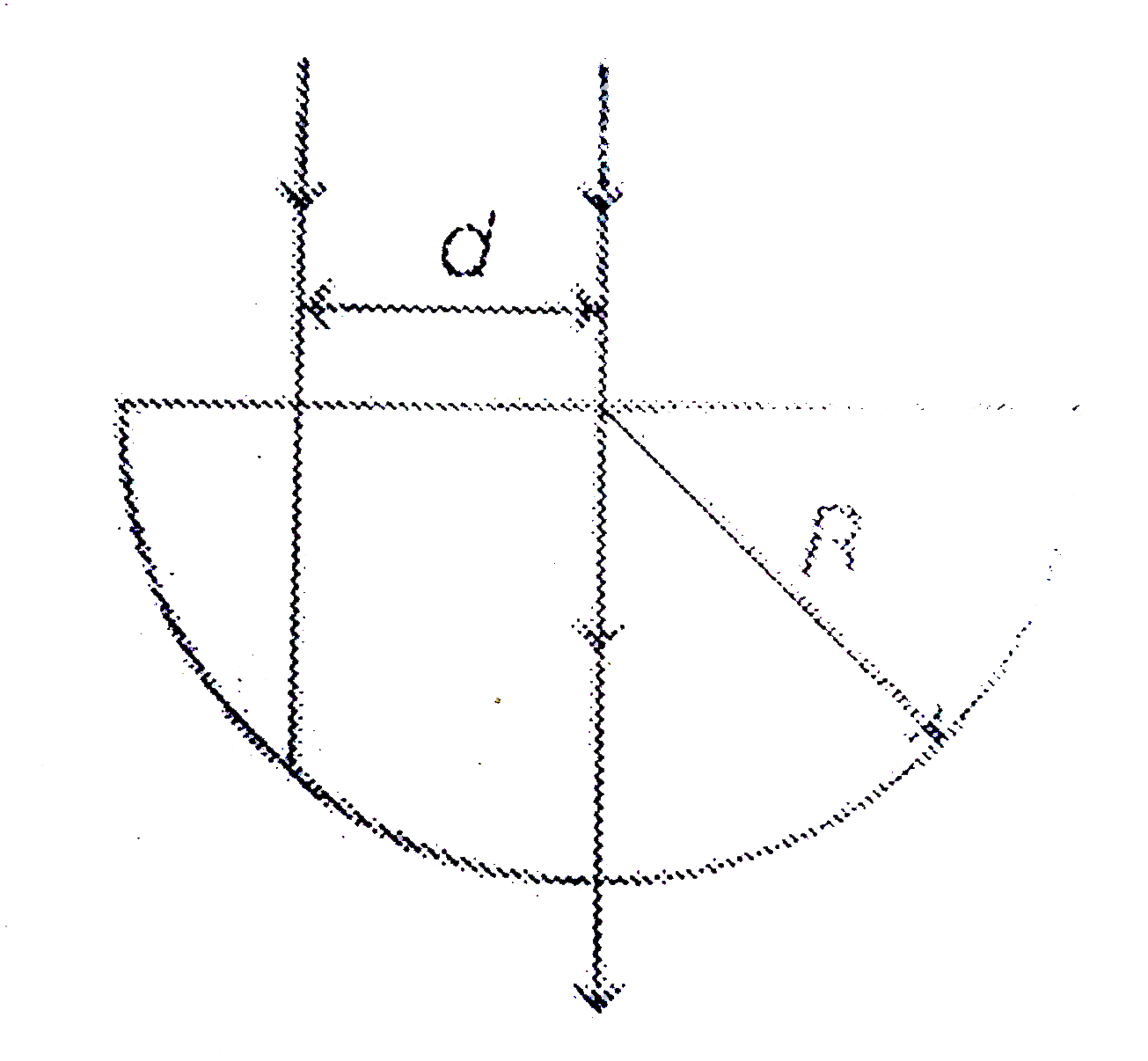 ARdBdRCR√R2−d2D√R2−d2R
ARdBdRCR√R2−d2D√R2−d2RA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
 AR2B3RCR3D2R
AR2B3RCR3D2R
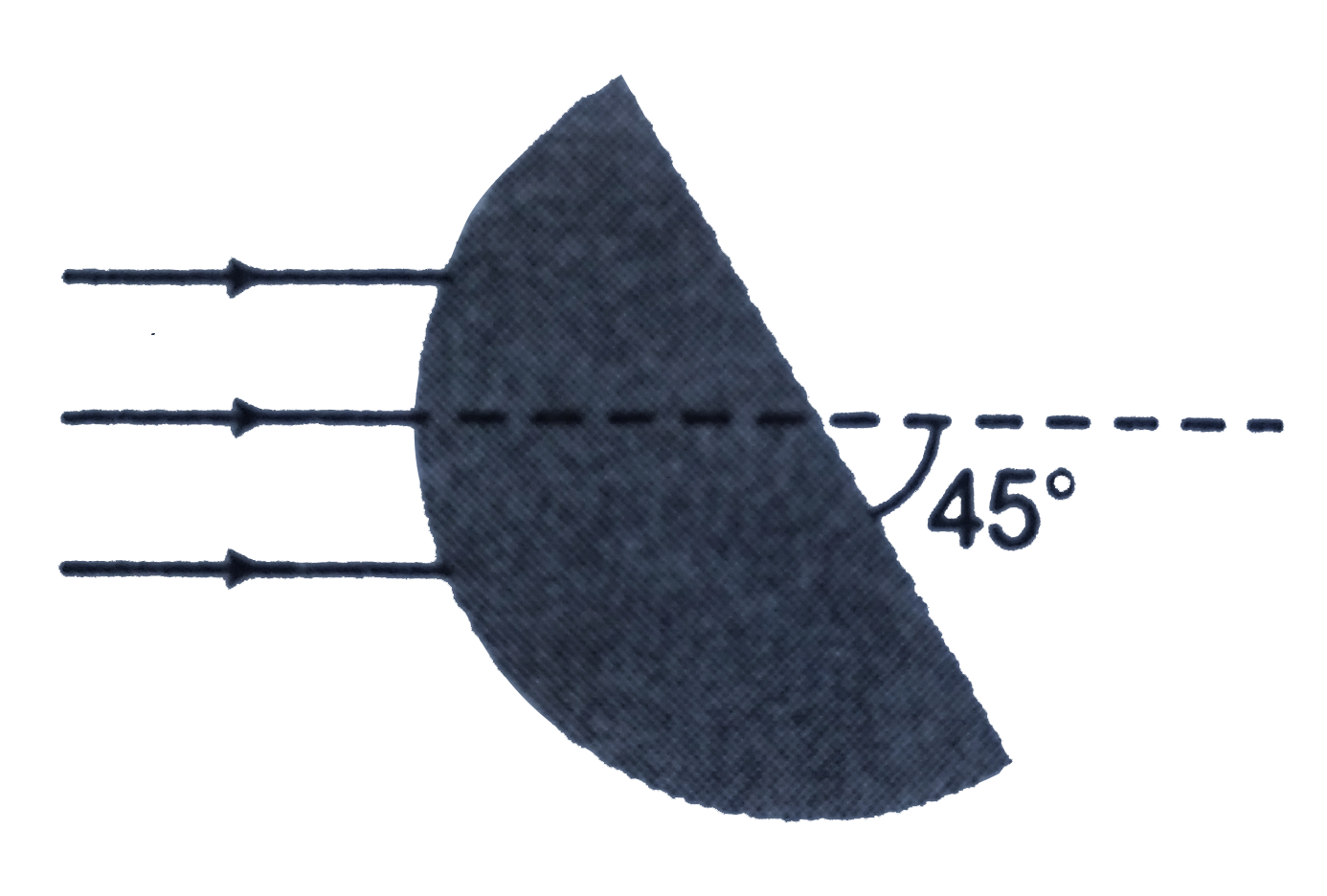
A light beam of diameter √3R is incident symmetrically on a glass hemispher of radius R and of refractive index n=√3 . Find radius of the beam at the base of hemispher.
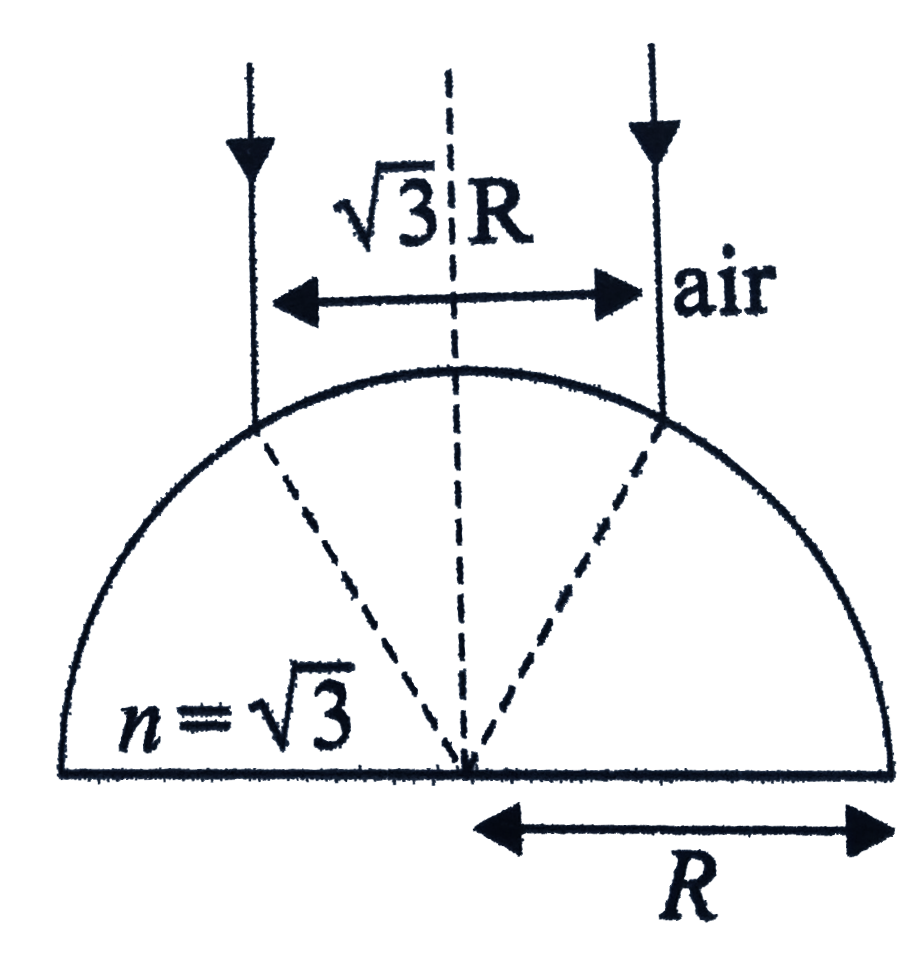
View SolutionA narrow parallel beam of light falls on a glass sphere of radius R and refractive index μ at normal incidence. The distance of the image from the outer edge is given by-
View SolutionA parallel beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index 2.0 as shown in figure. The position of the image formed by refraction at the first surface is :

View SolutionA glass prism in the shape of a quarter cylinder lies on a horizontal table. A uniform horizontal light beam falls on its vertical plane surface as shown in the figure. If the radius of the cylinder is R = 5cm and the refractive index of the glass is n = 1.5 where on the table beyond the cylinder will a path of light be found? (in cm) Light R
View SolutionA parallel beam of light is incident on a lens of focal length 10 cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. Find the distance of the final image from the lens.
 .
.
View Solution
