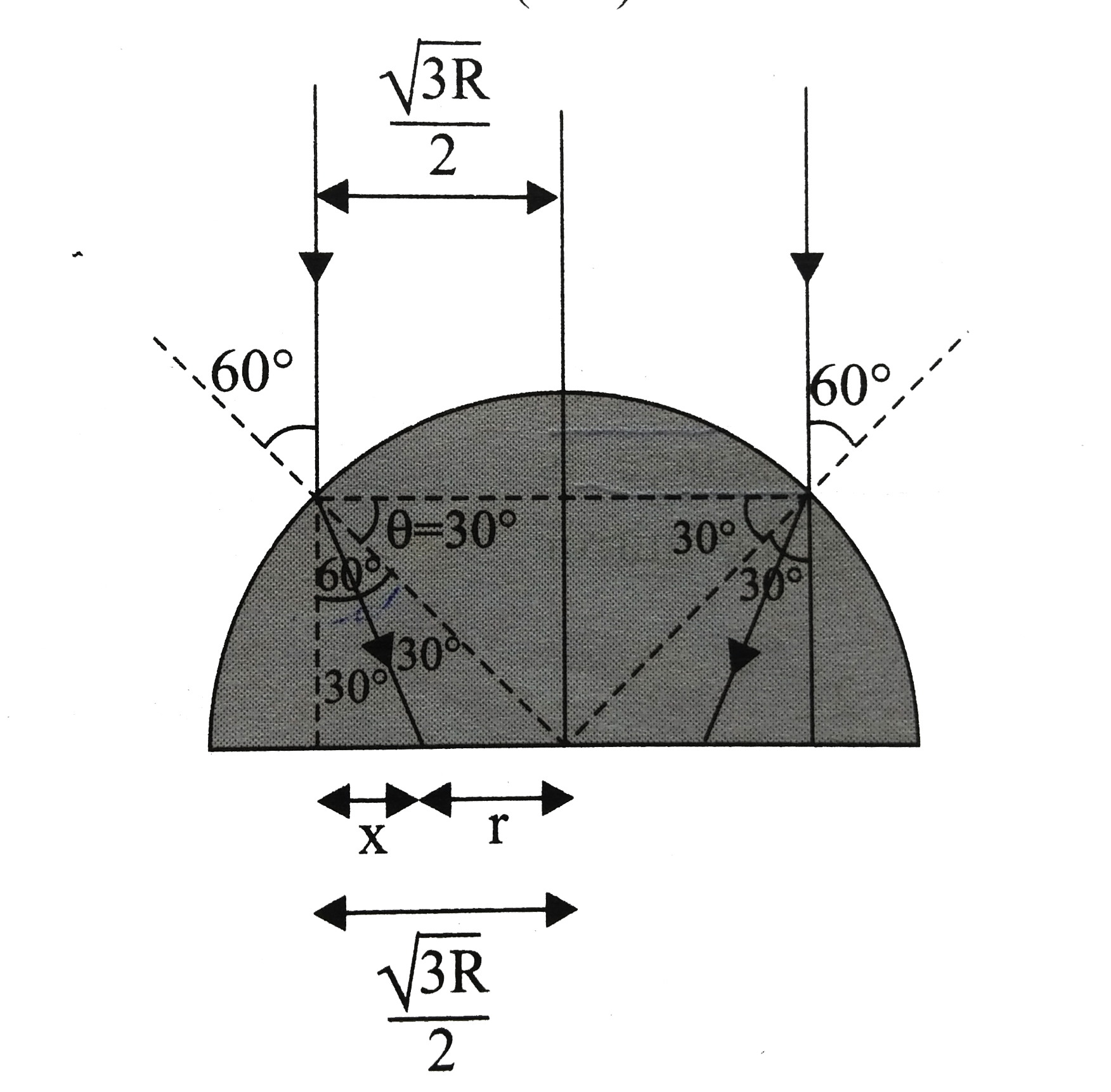
A light beam of diameter √3R is incident symmetrically on a glass hemispher of radius R and of refractive index n=√3 . Find radius of the beam at the base of hemispher.
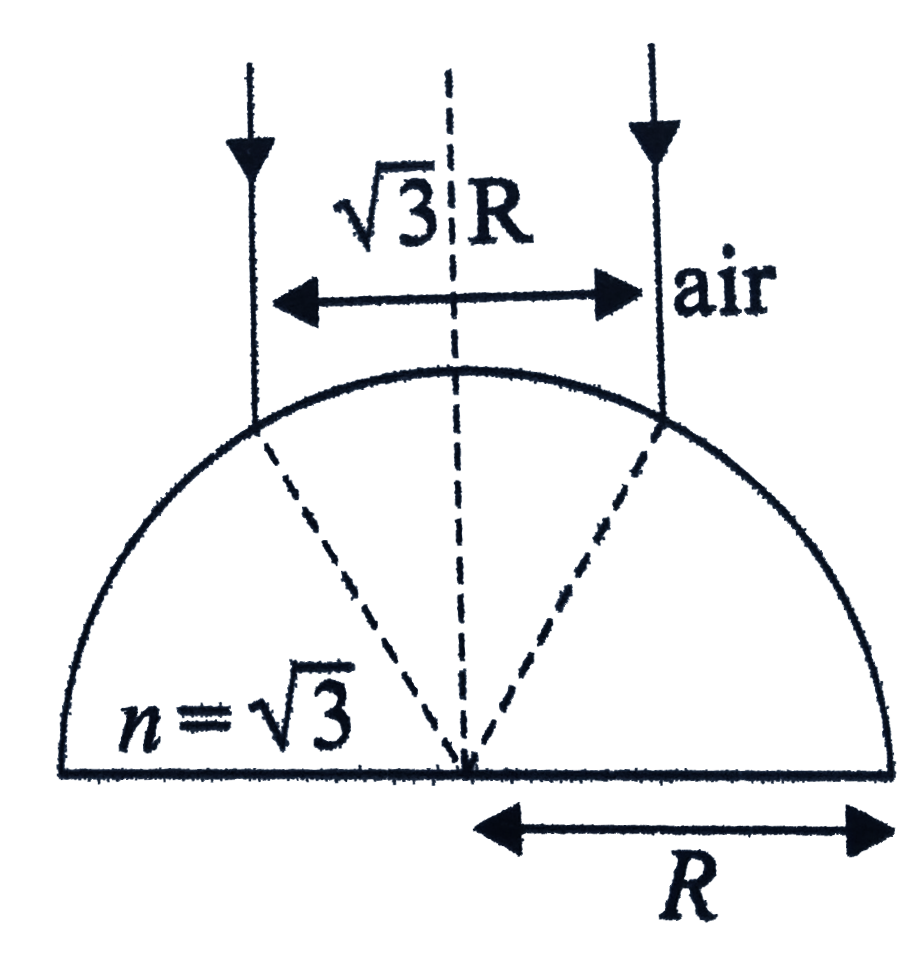
μ1sini=μ2sinr
1×sin60∘=√3×sinr,r=30∘
ΔMNPtan30∘=x/(R/2)
x=R2√3
r=√32R−x=√32R−R2√3
=(3−12√3)R=R√3
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.4
12 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.5
22 Videos
- GEOMETRICAL OPTICSBOOK - CENGAGE PHYSICSCHAPTER - GEOMETRICAL OPTICSEXERCISE - Exercise1.2
20 Videos
- FRICTIONBOOK - CENGAGE PHYSICSCHAPTER - FRICTIONEXERCISE - QUESTION BANK
1 Video
- GRAVITATIONBOOK - CENGAGE PHYSICSCHAPTER - GRAVITATIONEXERCISE - Question Bank
39 Videos
Similar Questions
A vertical beam of light of cross sectional radius R2 is incident symmetrically on the curved surface of a glass hemisphere of refractive index μ=32. Radius of the hemisphere is R and its base is on a horizontal table. Find the radius of luminous spot formed on the table. sin20∘=13 and sin80∘=0.98
View SolutionA horizontal ray of light is incident on a solid glass sphere of radius R and refractive index μ . What is net deviation of the beam when it emerged from the other side of the sphere?
View Solution
Knowledge Check
A beam of diameter 'd' is incident on a glass hemisphere as shown. If the radius of curvature of the hemisphere is very large in comparison to d, then the diameter of the beam at the base of the hemisphere will be
 A34dBdistance between object and screen is 90 cmCd3D23d
A34dBdistance between object and screen is 90 cmCd3D23dA parallel narrow beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index μ=1.5 as shown. The position of the image formed by refraction at the image formed by refraction at the spherical surface only as
 AR2B3RCR3D2R
AR2B3RCR3D2RA beam of diameter 'd' is incident on a glass hemisphere as shown in the figure. If the radius of curvature of the hemisphere is very large in comparision to d, then the diameter of the beam at the base of the hemisphere will be:
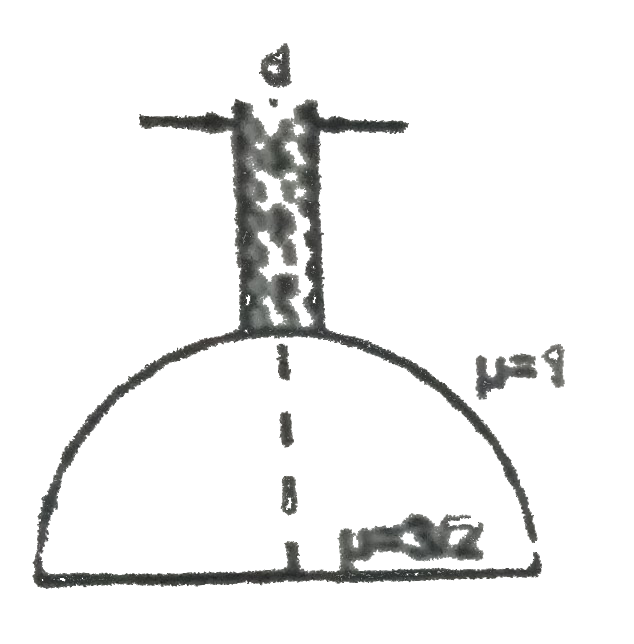 A34dBdCd3D23d
A34dBdCd3D23d
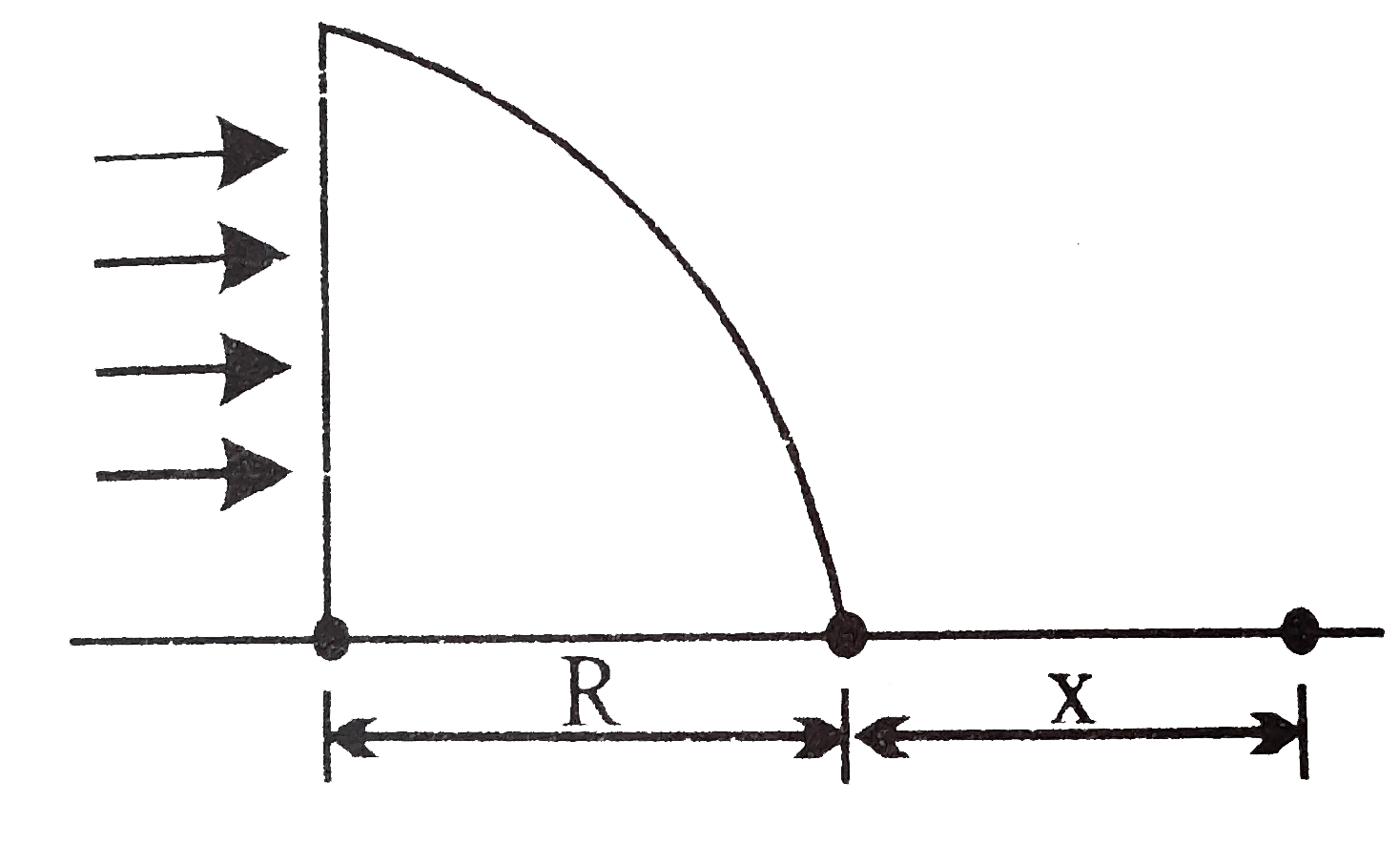
A uniform,horizontal beam of light is incident upon a quarter cylinder of radiusR=5cm and has a refractive index 2/√3.A patch on the table for a distance 'x'from the cylinder is unilluminated ,find the value of 'x'?
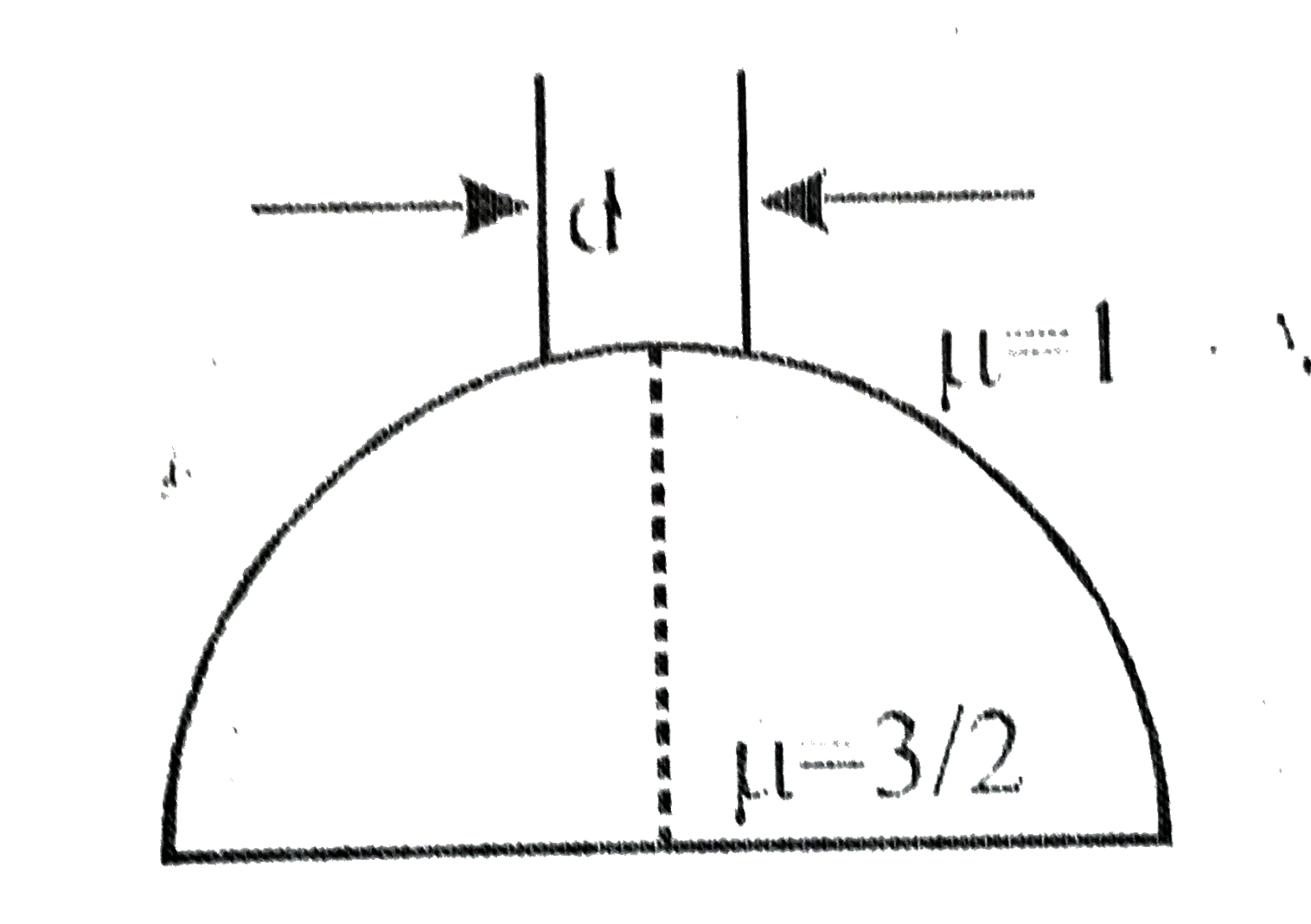
View SolutionA beam of diameter 'd' is incident on a glass hemisphere as shown. If the radius of curvature of the hemisphere is very large in comparison to d, then the diameter of the beam at the base of the hemisphere will be :
View SolutionA parallel beam of light is incident on the surface of a transparent hemisphere of radius R and refractive index 2.0 as shown in figure. The position of the image formed by refraction at the first surface is :

View SolutionA narrow parallel beam of light falls on a glass sphere of radius R and refractive index μ at normal incidence. The distance of the image from the outer edge is given by-
View SolutionA narror parallel beam of light is incident paraxially on a solid transparent sphere of radius r kept in air. What should be the refreative index if the beam is to be focusd (a) at the further surface of the sphere, (b) at the centre of the sphere.
View Solution