A lens placed between a candle and a fixed screen forms a real triply magnified image of the candle on the screen. When the lens is moved away form the candle by 0.8m without changing the position of the candle, a real image one-third the size of the candle is formed on the screen. Determine the focal length of the lens.
The correct Answer is:30 cm
Given- Distance between two position of the lens for image is formed
_E01_141_S01.png)
x=u2−u1=0.8 m (Given)
D=u1+v1
m1=v1u1=3⇒v1=3u1
v2u2=13⇒v2=u23
x=v1−u1=3u1−u1=0.8
u1=0.4∴v1=3×0.4=1.2
D=1.2+0.4−1.6
f=D2−x24D=(1.6)2−(0.8)24×1.6=0.3m=30cm
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[B]
18 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-05 (A)
35 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-3
12 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A convex lens is placed between an object and a screen which are at a fixed distance apart for one position of the lens. The magnification of the image obtained on the screen is m1. When the lens is moved by a distance d the magnification of the image obtained on the same screen m2, Find the focal length of the lens.
View SolutionA convex lens when placed in the first position forms a real image of an object on a fixed screen. The distance between the object and the screen is 75 cm. On displacing the lens from first position by 25 cm to the second position, again a real image is formed on the screen. Then the focal length of the lens is
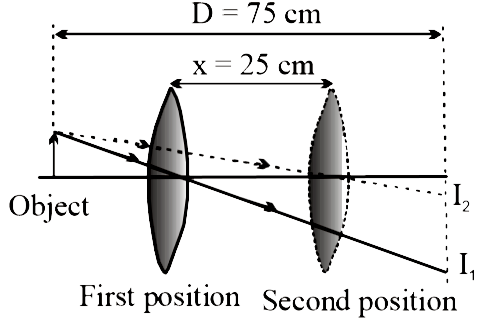
View Solution
Knowledge Check
A convex lens forms an image of an object on a screen 30 cm from the lens. When the lens is moved 90 cm towards the object, then the image is again formed on the screen. Then, the focal length of the lens is
A13 cmB24 cmC33 cmD40 cmA convex lens forms a real image 16 mm long on a screen. If the lens is shifted to a new position without disturbing the object or the screen then again a real image of length 81 mm is formed. The length of the object must be
A48.5 mmB36 mmC6 mmD72 mmA convex lens forms a real image on a screen placed at a distance 60 cm from the object. When the lens is shifted towards the screen by 20 cm , another image of the object is formed on the screen. The focal length of the lens is :
A45cmB40/3cmC30cmD12cm
A candle is placed 15cm in front of a lens. If the image of the candle captured on a screen is magnified two time, calculate the focal length and nature of the lens.
View SolutionThe height of the image formed by acoverign lens on a screen is8cm,For the same position of the object and the screen again an Image of size12.5cmis formed on the screen by shifting the lens.The height of the object.
View SolutionA convex lens produces an image of a real object on a screen with a magnification of 1/2. When the lens is moved 30 cm away from the object, the magnification of the image on the screen is 2. The focal length of the lens is
View SolutionA number of images of a candle flame are seen in thick mirror
View SolutionA convex lens can be fixed at two different positions between a burning candle and a screen so as to form sharp image of candle on the screen. If I1 and I2 be the size of the images respectively for the two positions of lens then the true size of the candle is given by
View Solution
