A narrow parallel beam of light is incident on a transparent sphere of refractive index $n$ if the beam finally gets focused at a point situated at a distance= $2 \times (radius of sphere)$ form the center of the sphere then find $n$ ?

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $\frac{4}{3}$

From (1) surface : $\frac{n}{v} - \frac{1}{\infty} = \frac{n - 1}{R}, v = \frac{n R}{n - 1}$
$\Rightarrow \frac{1}{R} - \frac{n}{v - 2 R} = \frac{1 - n}{- R}, \frac{2}{R} = \frac{n}{R} + \frac{n}{v - 2 R}$
$\frac{2}{R} = \frac{n (v - 2 R + R)}{R (v - 2 R)} \Rightarrow 2 v - 4 R = n v - n R$
On putting the value of v
$2 \frac{n R}{n - 1} - 4 R = \frac{n \times n R}{(n - 1)} = - n R$
2nR - 4nR + 4R = $n^{2} R - n^{2} R + n R, n = \frac{4}{3}$

|

Updated on:21/07/2023

Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRUMENTS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A parallel beam of light falls on a solid tranparent sphere.

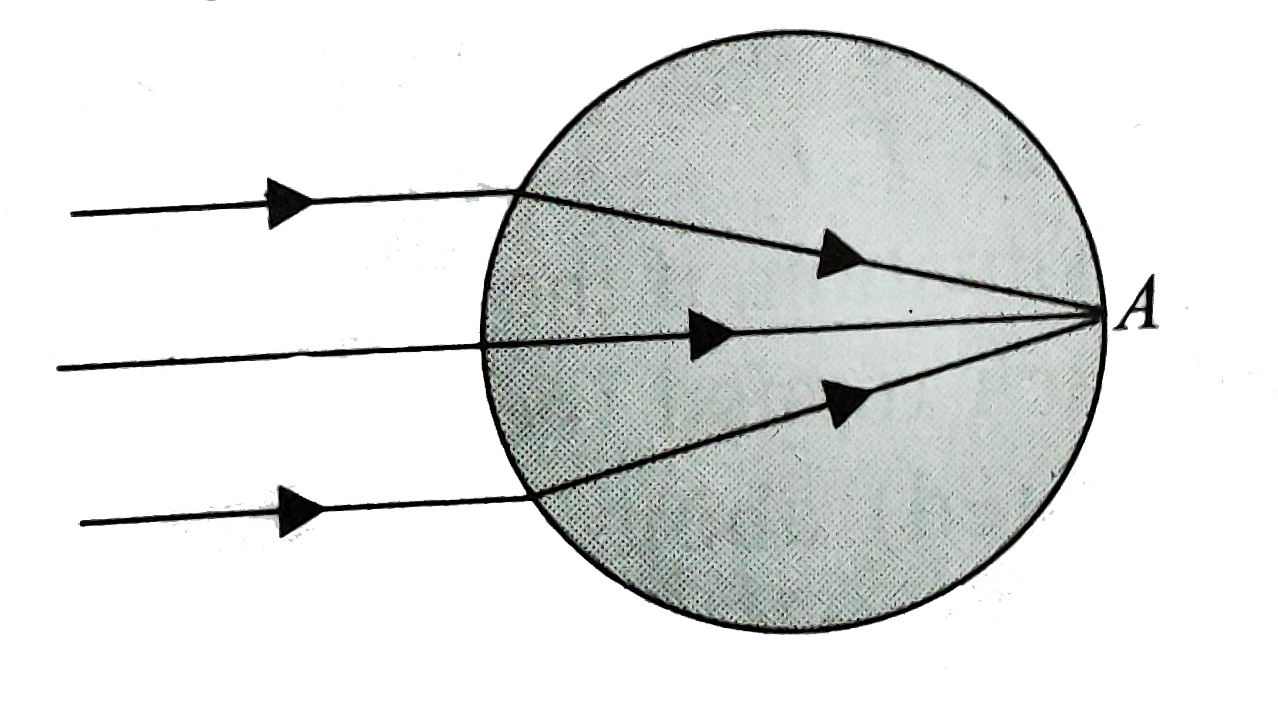
Q. Which is corret?
AIf the beam is thick, then whole beam can be focussed at A.
Bthe whole beam can be focussed at A only if the beam is thin enough
Cif the beam is thin, then the beam can't be focussed before A.
Dnone of these
Question 2 - Select One
A parallel beam of light falls on a solid tranparent sphere.

Q. For what value of refractive index $μ$ , the thin beam can be focussed at centre of sphere.
A1.5
B2
C2.5
Dnone of these
Question 3 - Select One
A parallel beam of light falls on a solid tranparent sphere.

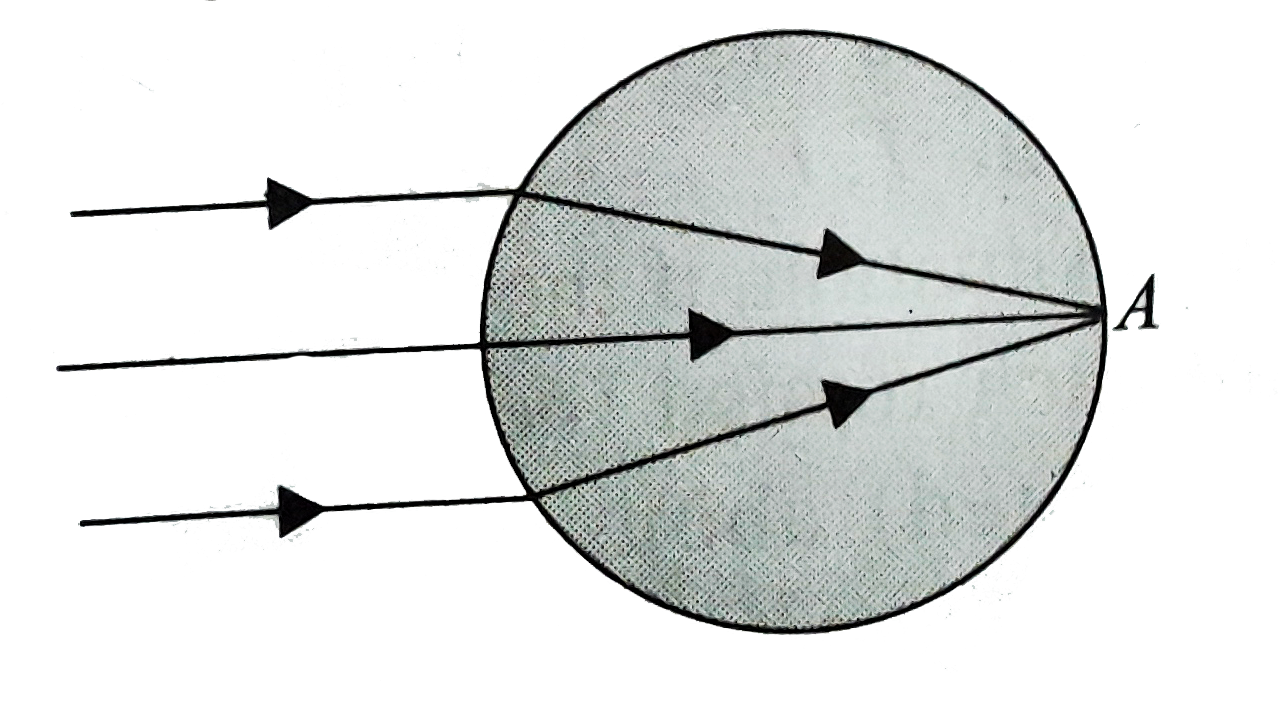
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,
A1.5
B1.7
C $2.0$
D2.5

ALLEN-GEOMETRICAL OPTICS-EXERCISE-04[A]

Home
Ask Doubt
Profile