What is the length of the image of the rod in mirror, according to the observer in air? (refractive index of the liquid is μ)
_E01_058_Q01.png)
μL+L
L+Lμ
Lμ+Lμ
None of these
The correct Answer is:B
_E01_058_S01.png)
When observer in rarer medium and objects is in denser medium then the length of immersed portion will be shorter (apparent) Hence length of image of rod in water =2L+μL−L=L+μL
Hence length of image of rod seen by observer in air is = L+μLμ=Lμ+L . Hence [B]
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-312videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[A]23videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE- 0145videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions427videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
A concave mirror has the form of a hemisphere with a radius of R=60cm A thin layer of an unknown transparent liquid is poured into the mirror ,The mirror-liquids system forms one real Image and another real image is formed by mirror alone ,with the souces ina certain position .One of them coincides with the source and the other is at distance of l=30cmfrom source.find the possible value(s) refractive index μof the liquid.
View SolutionAn equiconvex lens of refractive index μ1, focal length 'f' and radius of curvature 'R' is immersed in a liquid of refractive index μ2. For (i) μ2>μ1, and (ii) μ2<μ1, draw the ray diagrams in the two cases when a beam of light coming parallel to the principal axis is incident on the lens. Also find the focal length of the lens in terms of the original focal length and the refractive index of the glass of the lens and that of the medium.
View Solution
Knowledge Check
- Question 1 - Select One
The focal length of a glass lens in air is f. When immersed in water (refractive index μ) its focal length would be
AfB<fC>fDnothing can be decided - Question 2 - Select One
A thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its priincipal axis, the object coincides with its own image.
Q. If another liquid is filled instead of water, the object and the image coincide at a distance 25 cm from the lens.
Calculate the refractive index of the liquid.A1.6B2.6C2.8D3.2 - Question 3 - Select One
A circular beam of light (diameter d) falls on a plane surface of a liquid. The angle of incidence is 45∘ and refractive index of the liquid is μ. The diameter of the refracted beam is
AdB(μ−1)dC√2μ2−1ddD√μ2−1μd
An equiconvex lens μ=(3)/(2) is placed over a plane mirror as indicated in diagram. An object placed "12cm" from system such that image and object coincide.Now a liquid is poured between mirror and lens and for the same object the image now formed at "24cm" from mirror.The refractive index of the liquid poured will be
View SolutionIn previous illustrations if image formed by the mirror coincides with the source and that produced by the combination is produced at a distance 30 cm from the source away from mirror then find the refractive index of the liquid.
View SolutionA light ray passes from air into a liquid as shown in figure. Find refractive index of liquid.
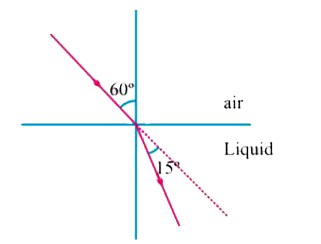
View SolutionA glass lens of refractive index 1.45 disappears when immersed in a liquid. What is the value of refractive index of the liquid ?
View SolutionA thin equiconvex lens of refractive index 3/2 is placed on a horizontal plane mirror as shown in figure. The space between the lens and the mirror is filled with a liquid of refractive index 4/3 . It is found that when a point object is placed 15 cm above the lens on its principal axis, the object coincides with its own image.
Q. If another liquid is filled instead of water, the object and the image coincide at a distance 25 cm from the lens.
Calculate the refractive index of the liquid.View Solution