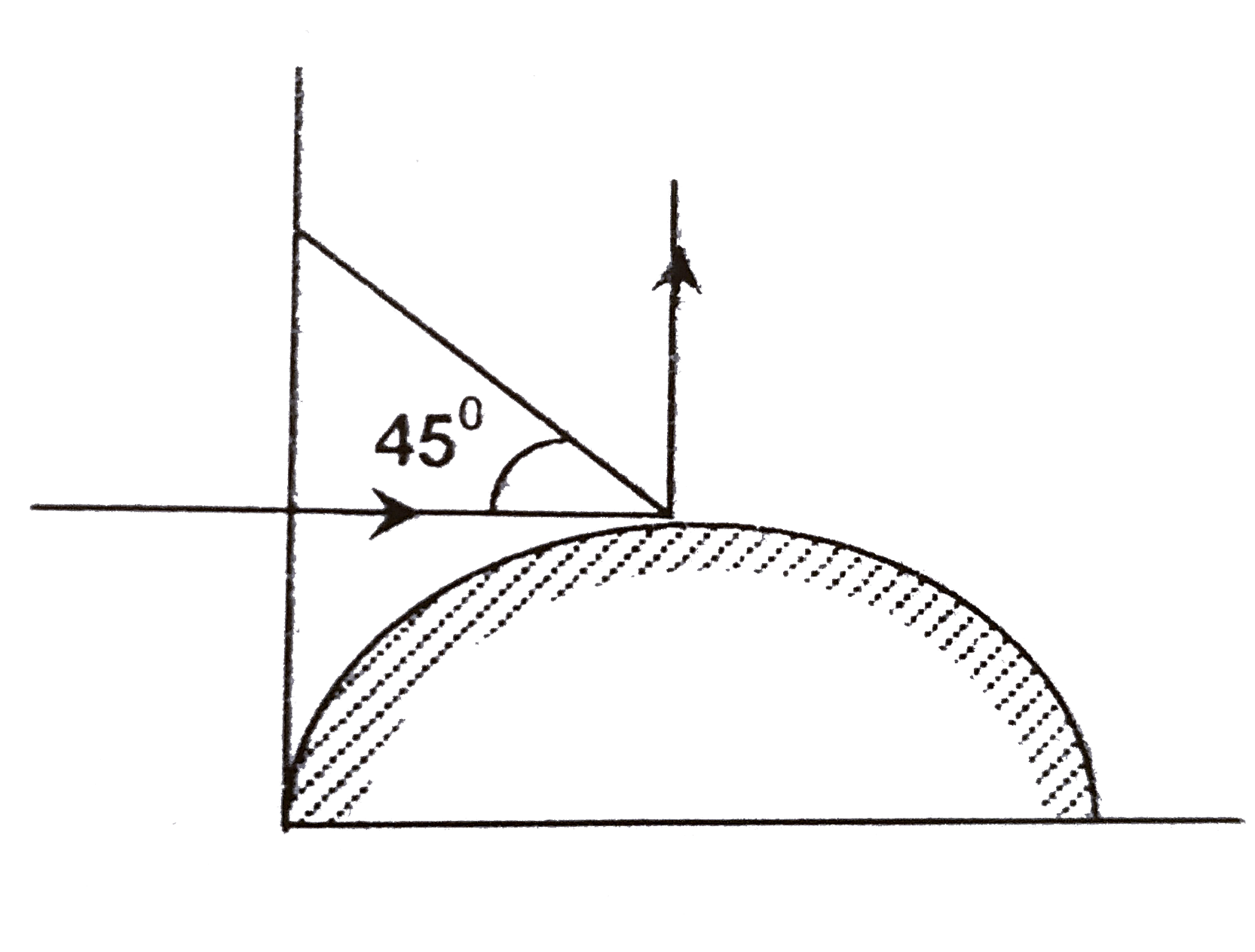
If the equation of mirror is given by $y = 2 / π sin π x (y > 0, 0 \leq x \leq 1$ ) then find the point on which horizontal ray should be incident so that the reflected ray become perpendicular to the incident ray

A

$(\frac{1}{3}, \frac{\sqrt{3}}{π})$

B

$(\frac{\sqrt{3}}{π}, \frac{1}{3})$

C

$(\frac{2}{3}, \frac{\sqrt{3}}{π})$

D

$(1, 0)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A,C

$y = \frac{2}{π} sin π x, \frac{d y}{d x} = \frac{2}{π} cos π \times π \Rightarrow \frac{d y}{d x} = \pm 1$
$tan 45^{\circ} = 1 = 2 cos π x$
$cos π x = \frac{1}{2} \Rightarrow π x = \frac{n π}{3} ∴ x = \frac{1}{3} and \frac{2}{3}$
$∴ y = \frac{2}{π} \times \frac{\sqrt{3}}{2} (∵ sin π \times \frac{1}{3} = \frac{\sqrt{3}}{2}) = \frac{\sqrt{3}}{π}$

|

Updated on:21/07/2023

Class 12 PHYSICS RAY OPTICS AND OPTICAL INSTRUMENTS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A reflecting surface is represented by the equation
$y = \frac{2 L}{π} sin (\frac{π x}{L})$ , where $0 \leq x \leq L$ . A ray of light travelling horizontally becomes vertical after reflection with the surface. The co-ordinates of the point where this ray is incident is.

A $(\frac{L}{4}, \frac{\sqrt{2} L}{π})$
B $(\frac{L}{3}, \frac{\sqrt{3} L}{π})$
C $(\frac{3 L}{4}, \frac{\sqrt{2} L}{π})$
D $(\frac{2 L}{3}, \frac{\sqrt{3} L}{π})$
Question 2 - Select One or More
A plane mirror, reflecting a ray of incident light, is rotated through an angle $θ$ about an axis through the point of incidence in the plane of the mirror perpendicular to the plane of incidence, then
AThe reflected ray does not rotate
BThe reflected ray rotates through an angle $θ$
CThe reflected ray rotates through an angle $2 θ$
DThe incident ray is fixed
Question 3 - Select One
A plane mirror, reflecting a ray of incident light, is rotated through an angle $θ$ about an axis through the point of incidence in the plane of the mirror perpendicular to the plane of incidence, then
AThe reflected ray does not rotate.
BThe reflected ray rotates through an angle $θ .$
CThe reflected ray rotates through an angle $2 θ .$
DNone of these

ALLEN-GEOMETRICAL OPTICS-EXERCISE-2

Home
Ask Doubt
Profile