Shown plane mirror is lying in y-z plane. A particle P has velocity →u=5ˆi+6ˆj at t=0 & acceleration →a=2tˆj. Velocity of its image at t=2s relative to it is
_E01_050_Q01.png)
10ˆi
−10ˆi
20ˆj
−20ˆj
The correct Answer is:B
vI=2vM−v0
= 2×0−(5ˆi+(6+2t)ˆj)
vI=−5ˆi+10ˆj,v10=vI−v0
hence vIo=−5ˆi+10ˆj−(5ˆi+10ˆj)
[ at t= 2 sec] = −10ˆi
_E01_050_S01.png)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-3
12 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[A]
23 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE- 01
45 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Knowledge Check
A particle has an initial velocity of 4ˆi+3ˆj and an acceleration of 0.4ˆi+0.3ˆj. Its speed after 10s is
A10 unitsB7 unitsC7√2 unitsD8.5 unitsA particle has an initial velocity of 3ˆi+4ˆj and on acceleration of 0.4ˆj+0.3ˆj . The magnitude of its velocity after 10 s is
A7√2 unitsB7 unitsC8.5 unitsD10 units .A particle has an initial velocity 3ˆi+4ˆj and an accleration of 0.4ˆi+0.3ˆj. Its speed after 10s is
A10 unitB7 unitsC7√2 unitsD8.5 units
A particle is given an initial velocity of →u=(3ˆi+4ˆj)m/s. Acceleration of the particle is →a=(3t2+2tˆj)m/s2. Find the velocity of particle at t=2s.
View SolutionA particle is moving in an isolated x−y plane. At an instant, the particle has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2. At that instant what will be the radius of curvature of its path ?
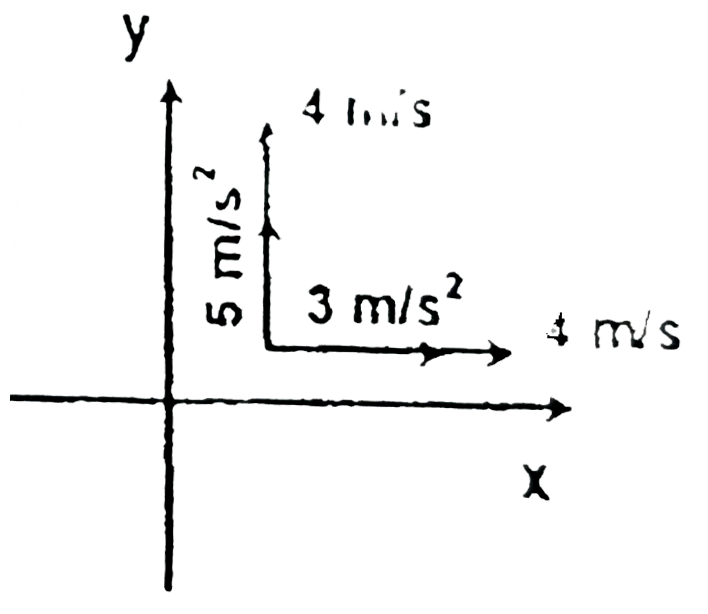
View SolutionA particle has initial velocity (2ˆi+3ˆj) and acceleration (0.3ˆi+0.2ˆj). The magnitude of velocity after 10 second will be
View SolutionA particle moves in plane with acceleration →a=2ˆi+2ˆj. If →v=3ˆi+6ˆj, then final velocity of particle at time t=2s is
View SolutionThe position of a particle moving in x-y plane changes with time t given by →x=3t2ˆi+9tˆj. The acceleration of particle would be
View Solution