A system of coordinatees is drawn in a medium whose refractive index vaires as μ=21+Y2 where 0≤y≤1. A ray of light is incident at origin at an angle 60∘ with y-axis as shown in figure. At point P, the ray becomes parallel to x-axis, the volue of H is -

{(2√3)−1}1/2
{2√3}1/2
{(√3)−1}1/2
(4√3−1}1/2
The correct Answer is:A
μsinθ1=μ2sinθ2⇒ at origin x =0 , y=0 ⇒μ=2&θ=60∘
at point P:θ=90∘⇒2sin60∘=μsin90∘⇒√3=2y2+1⇒y=[(2√3)−1]1/2
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
The refractive index of an anisotropic medium varies as μ=μ0√(x+1) , where 0≤x≤a. A ray of light is incident at the origin just along y-axis (shown in figure). Find the equation of ray in the medium .
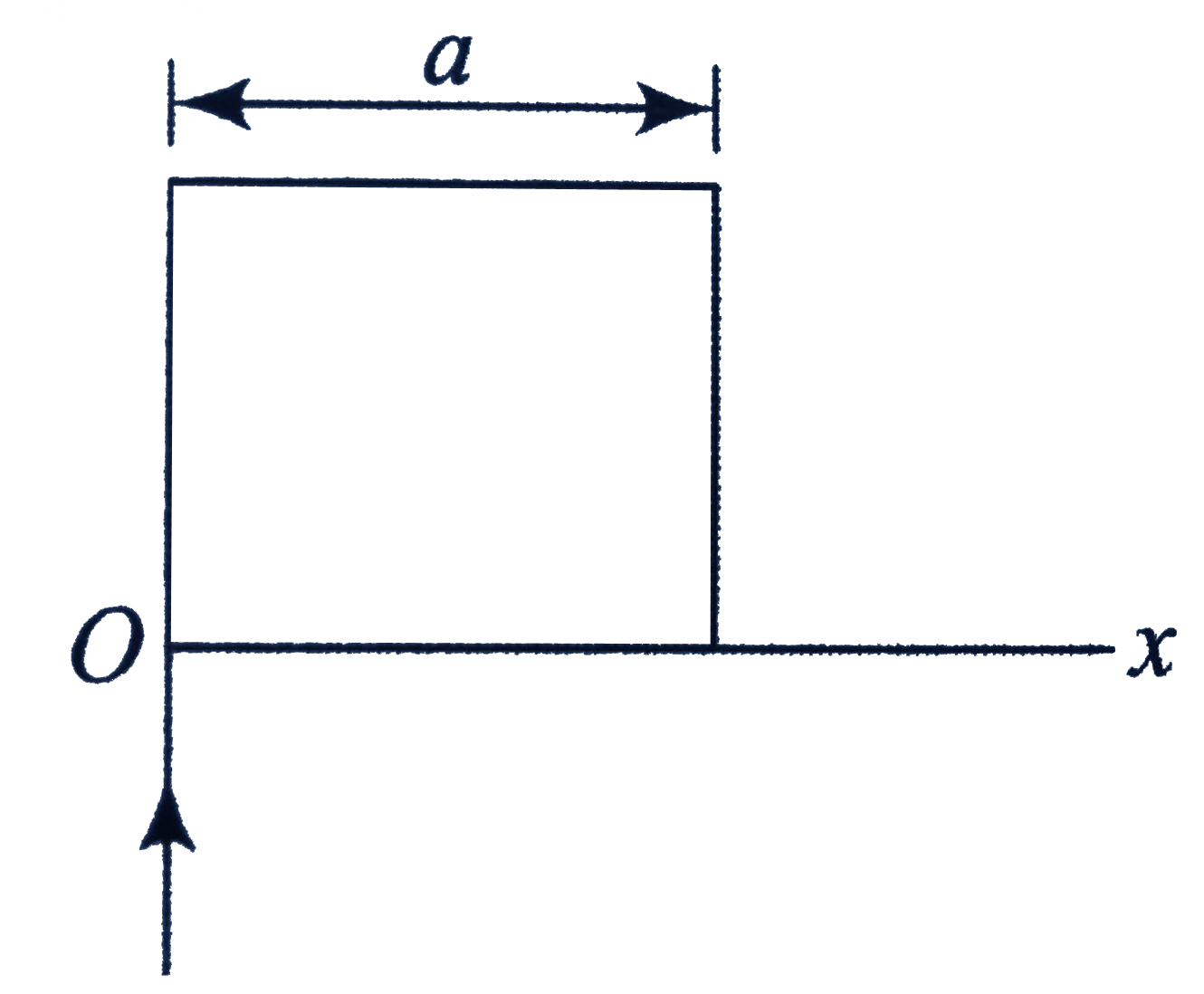
View SolutionA ray of light coming from origin after reflectiion at the point P(x,y) of any curve becomes parallel to x-axis, the , equation of the curve may be :
View Solution
Knowledge Check
A light ray enters into a medium whose refractive index varies along the x-axis as n(x)=n0√1+x4 where n0=1. The medium is bounded by the plates x=0,x=1 & y=0. It the ray enters at the origin at an angle 30∘ with x-axis
 Aequation of trajectory of the light ray is y=[√3+x−√3]Bequation of trajectory of the light ray is y=2[√3+x−√3]Cthe coordinate the point at which light ray comes out from the medium is [1,2(2−√3)]Dthe coordinate the point at which light ray comes out from the medium is [0,2(2−√3)]
Aequation of trajectory of the light ray is y=[√3+x−√3]Bequation of trajectory of the light ray is y=2[√3+x−√3]Cthe coordinate the point at which light ray comes out from the medium is [1,2(2−√3)]Dthe coordinate the point at which light ray comes out from the medium is [0,2(2−√3)]A ray of light refracts from medium 1 into a thin layer of medium 2, crosses the layer and is incident at the critical angle on the interface between the medium 2 and 3 as shown in the figure. If the angle of incidence of ray is θ, the values of θ is
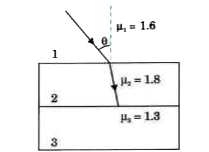 Asin−1(89)Bsin−1(1318)Csin−1(1316)Dsin−1(813)
Asin−1(89)Bsin−1(1318)Csin−1(1316)Dsin−1(813)
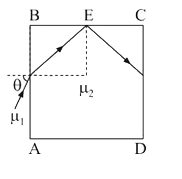
A transparent cube of side d, made of a material of refractive index μ2 , is immersed in a liquid of refractive index μ1(μ1<μ2). . A ray is incident on the face AV at an angle θ (shown in the figure). Total internal refraction takes place at point E on the face BC. Then must satisfy:
View Solutionx-y plane separates two media, z≥0 contains a medium of refractive index 1 and z≤0 contains a medium of refractive index 2. A ray of light is incident from first medium along a vectorˆi+ˆj−ˆk. Find the unit vector along the refracted ray.
View SolutionA spherical surface of radius R separates air from a medium of refractive index μ. Parallel beam of light is incident, from medium side, making a small angle θ with the principal axis of the spherical surface. Find the co-ordinates of the point where the rays will focus in air.
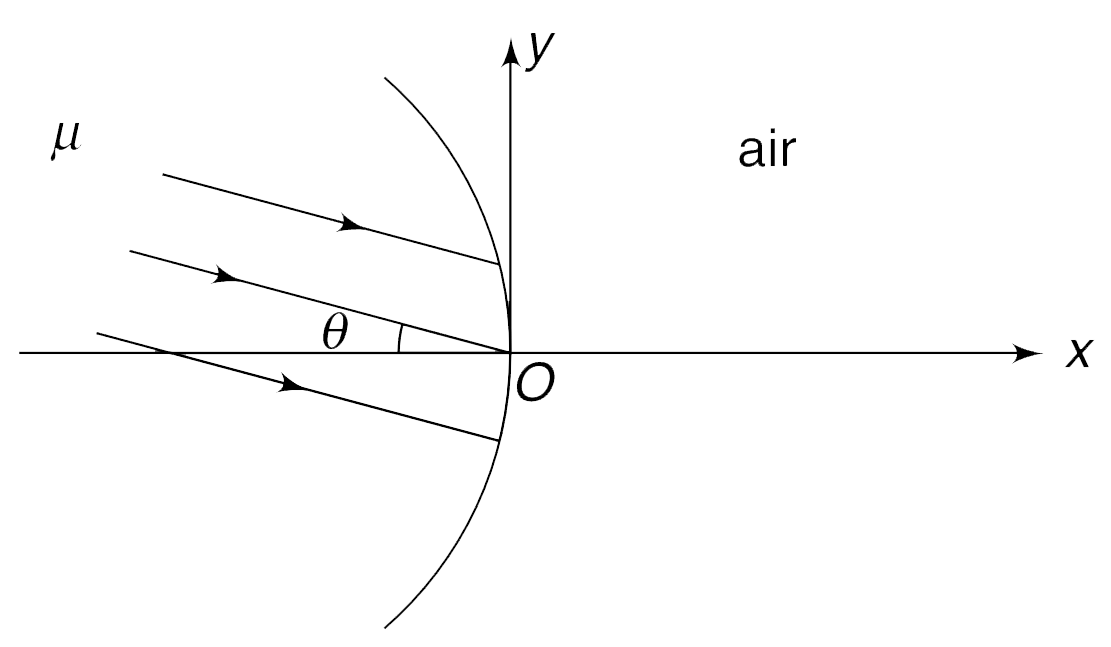
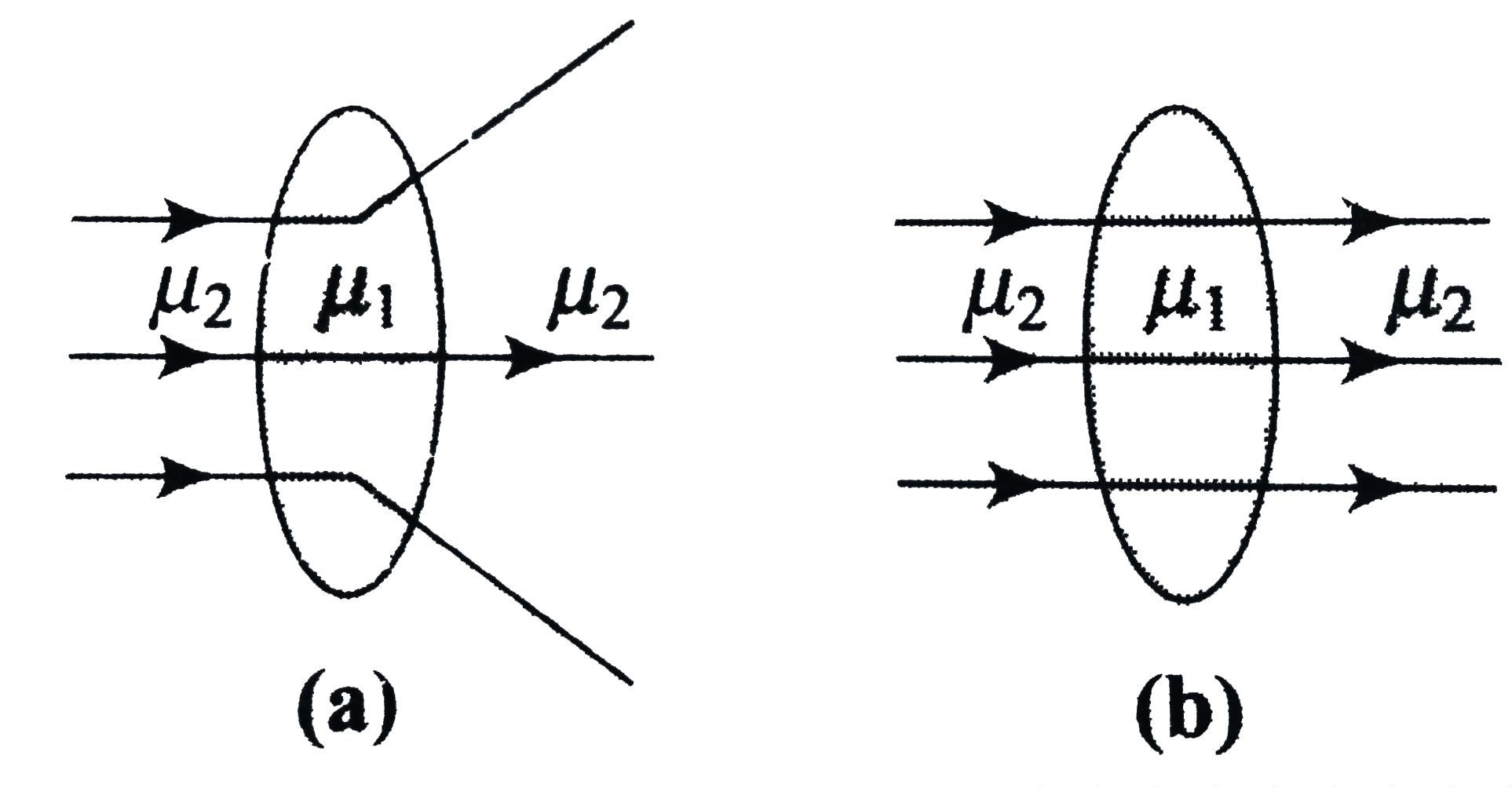
View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
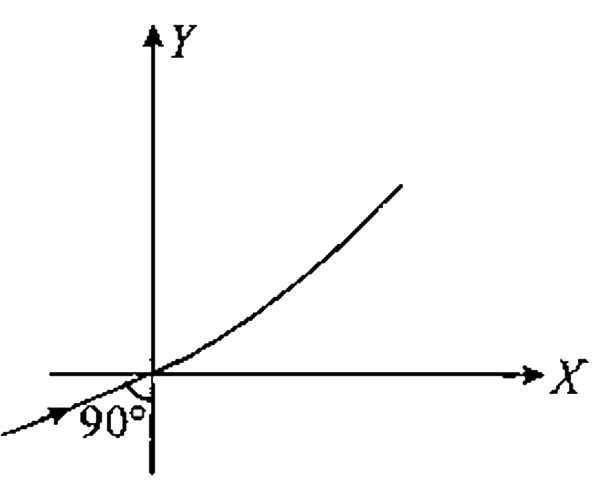
View SolutionFind the variation of Refractive index assuming it to be a function of y such that a ray entering origin at grazing incident follows a parabolic path y=x2 as shown in figure.
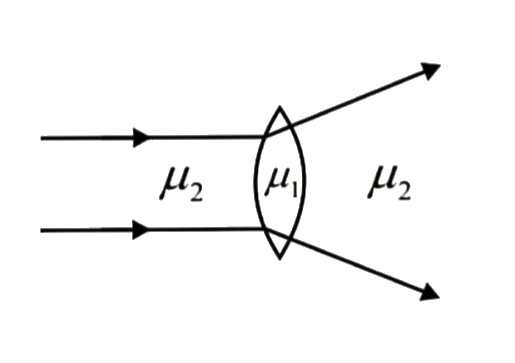
View SolutionA thin bi-convex lens made out of a material of refractive index μ1 is place in a medium of refractive index μ2. A paraxial beam of light, parallel to the principal axis of the lens, is shown in the figure. Based on the ray diagram, we can conclude that
View Solution
