Find the variation of Refractive index assuming it to be a function of y such that a ray entering origin at grazing incident follows a parabolic path y=x2 as shown in figure.
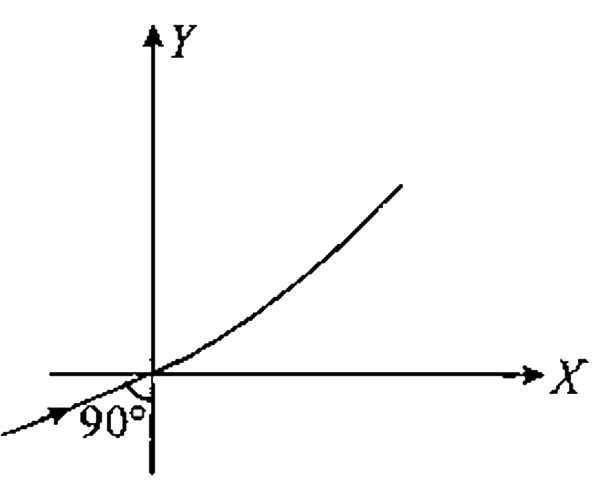
Step by step video & image solution for Find the variation of Refractive index assuming it to be a function of y such that a ray entering origin at grazing incident follows a parabolic path y = x^(2) as shown in figure. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Practive Exercise 5.1
10 Videos
- GEOMETRICAL OPTICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - GEOMETRICAL OPTICSEXERCISE - Practive Exercise 5.2
6 Videos
- ELECTROSTATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - ELECTROSTATICSEXERCISE - Unsolved Numberical Problems
73 Videos
- HEAT AND THERMAL EXPANSIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - HEAT AND THERMAL EXPANSIONEXERCISE - UNSOLVED NUMRICAL PROBLEMS FOR PREPARATION OF NSEP, INPhO & IPhO
82 Videos
Similar Questions
A prism has refracting angle equal to π/2. It is given that γ is the angle of minimum deviation and β is the deviation of the ray entering at grazing incidence. Prove that sinγ=sin2β .
View SolutionA prism of angle A and refractive index 2 is surrounded by medium of refractive index √3 . A ray is incident on side PQ at an angle of incidence i(0≤i≤90∘) as shown in the figure-. The refracted ray is then incident on side PR of prism. The minimum angle A of prism for which ray incident on side PQ does not emerge out of prism from side PR (for any value of i) is:
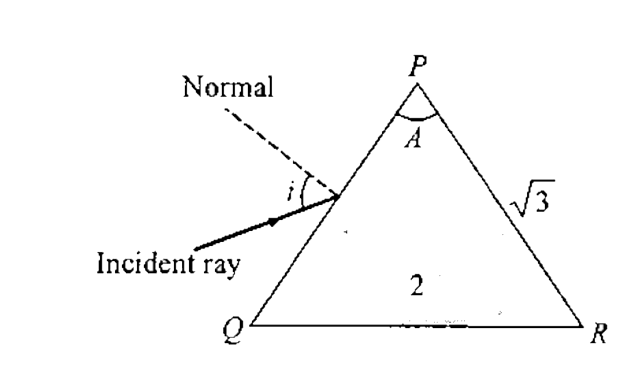
View Solution
Knowledge Check
A ray of light enters a spherical drop of water of refractive index μ as shown in figure.
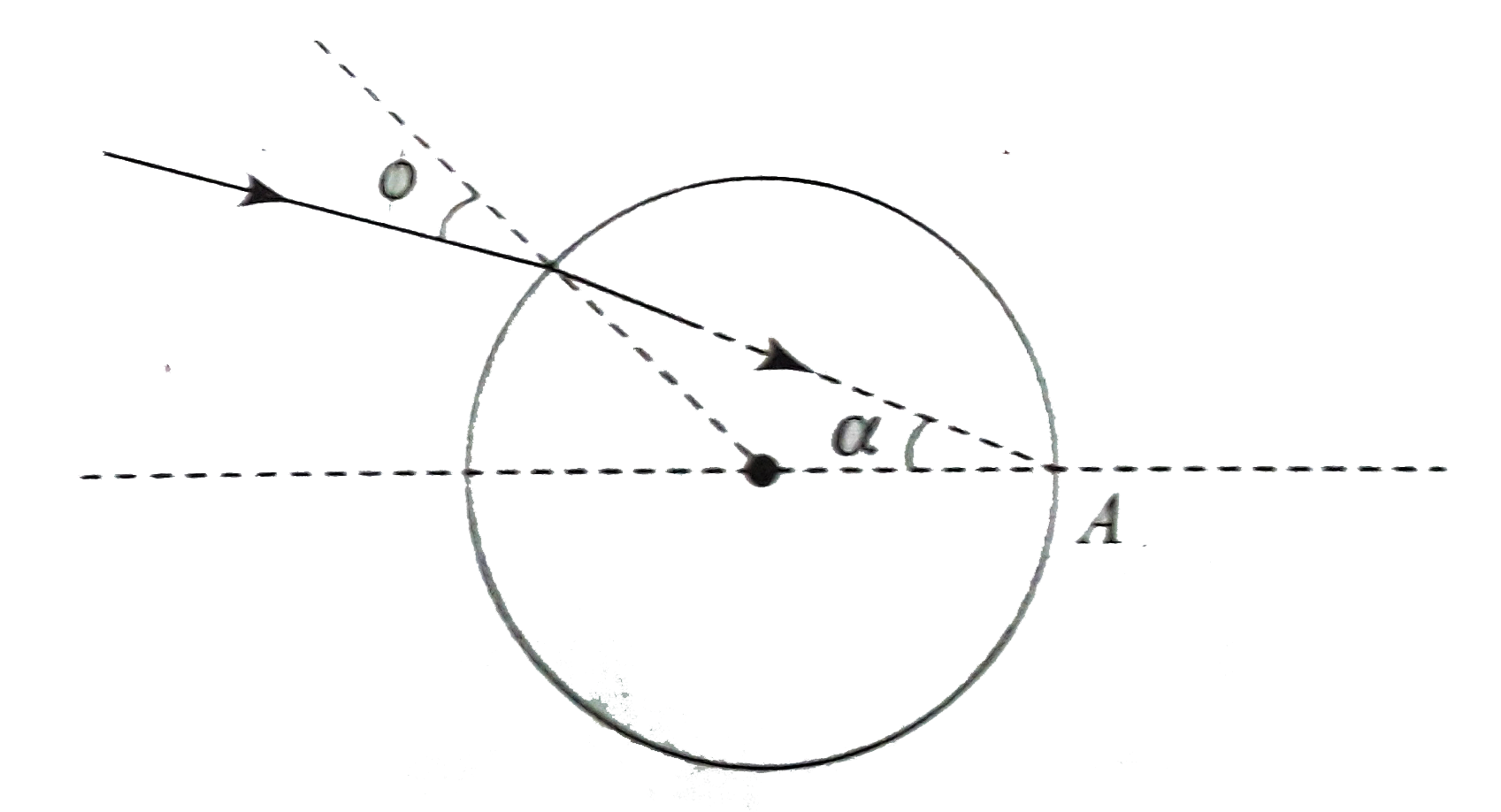
Q. An expression of the angle between incident ray and emergent ray (angle of deviation) as shown in figure.
 A0∘BϕCα−ϕDπ−4α+2ϕ
A0∘BϕCα−ϕDπ−4α+2ϕA ray of light enters a spherical drop of water of refractive index p as shown in the figure.
An expression of the angle between incidence ray and emergent ray (angle of deviation) as shown in the figure is

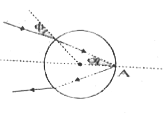 A0∘BϕCα−ϕDπ−4α+2ϕ
A0∘BϕCα−ϕDπ−4α+2ϕA system of coordinatees is drawn in a medium whose refractive index vaires as μ=21+Y2 where 0≤y≤1. A ray of light is incident at origin at an angle 60∘ with y-axis as shown in figure. At point P, the ray becomes parallel to x-axis, the volue of H is -
 A{(2√3−1)}1/2B{2√3}1/2C{(√3−1)}1/2D{√(3)+1}1/2
A{(2√3−1)}1/2B{2√3}1/2C{(√3−1)}1/2D{√(3)+1}1/2

A ray is incident on a sphere of refractive index √2 as shown in figure. Angle of refraction of the ray inside sphere is 30∘ if total deviation suffered by the ray is 30x0, then find x.
View SolutionA transparent solid cylinderical rod has a refractive index of 2√3. It is surrounded by air. A light ray is incident at the mid-point of one end of the rod as shown in the figure. The incident angle θ for which the light ray grazes along the wall of the rod is

View SolutionA transparent solid cylinder rod has a refractive index of 2√3It is surrounded by air. A light ray is incident at the mid point of one end of the rod as shown in the figure.
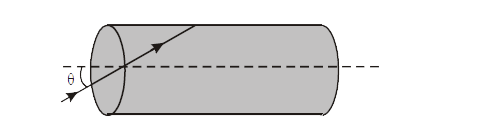
The incident angle θ for which the light ray grazes along the wall of the rod is
View SolutionA transparent solid cylinder rod has a refractive index of 2√3. It is surrounded by air. A light ray is incident at the mid point of one end of the rod as shown in the figure.
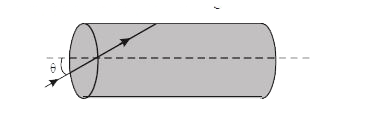
The incident angle θ for which the light ray grazes along the wall of the rod is
View SolutionA transparent solid cylindrical rod has a refractive index of 2√3 .It is surrounded by air. A light ray is incident at the mid-point of one end of the rod as shown in the figure. The incident angle θ for which the light ray grazes along the wall of the rod is:
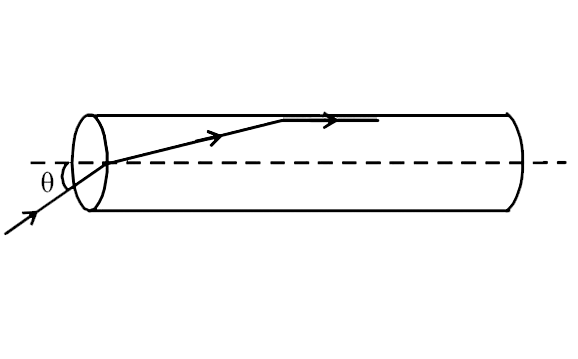
View Solution
