The variation of lengths of two moles rods A and B with change in temperature is shown in figure . The ratio of αaαB is :-
_E01_013_Q01.png)
32
23
43
34
The correct Answer is:B
l=l0(1+αΔT)⇒l−l0=l0αΔT
⇒l0αAΔTl0αBΔT=104−100106−100=46⇒αAαB=23
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -03
11 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - SOME WORKED OUT EXAMPLES
84 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - All Questions
427 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
The variation of lengths of two metal rods A and B with change in temperature are as shown in the figure. The ratio of αBαA is (Here αA= Linear coefficient of thermal expansion of rod A3αB= Linear coefficient of thermal expansion of rodB .
'(##CEN_KSR_PHY_JEE_C13_E01_016_Q04##)'
View SolutionA metal cylinder of radius R is placed on a wooden plank BD. The plank is kept horizontal suspended with the help of two identical string AB and CD each of length L. The temperature coefficient of linear expansion of the cylinder and the strings are a1 and a2 respectively. Angle q shown in the figure is 30∘. It was found that with change in temperature the centre of the cylinder did not move. Find the ratio α1α2 , if it is know that L = 4R. Assume that change in value of θ is negligible for small temperature changes

View Solution
Knowledge Check

The variation of length of two metal rods A and B with change in temperature is shown in Fig. the coefficient of linear expansion αA for the metal A and the temperature T will beAαA=3×10−6/∘C,500∘CBαA=3×10−6/∘C,222.22∘CCαA=27×10−6/∘C,500∘CDαA=27×10−6/∘C,222.22∘CTwo different rods A and B are kept as shown in figure . The variation of temperature of different cross sections with distance is plotted in a graph shown in figure . The ration of thermal conductivities of A andB is -
_E01_027_Q01.png) A2B0.5C1D2/3
A2B0.5C1D2/3An isosceles triangle is formed with a thin rod of length l1 and coefficient of linear expansion α1, as the base and two thin rods each of length l2 and coefficient of linear expansion α2 as the two sides. The distance between the apex and the midpoint of the base remain unchanged as the temperature is varied. the ratio of lengths l1l2 is
 A2√α1α2B√α2α1C2√α2α1D12√α2α1
A2√α1α2B√α2α1C2√α2α1D12√α2α1
Two different metal bodies A and B of equal mass are heated at a uniform rate under similar conditions. The variation of temperature of the bodies is graphically represented as shown in the figure. The ratio of specific heat capacities is :
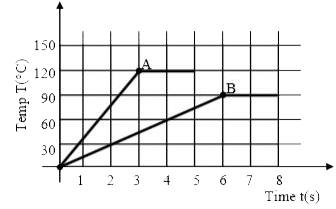
View SolutionThe variation of vapour pressure of different liquids with temperature is shown in figure
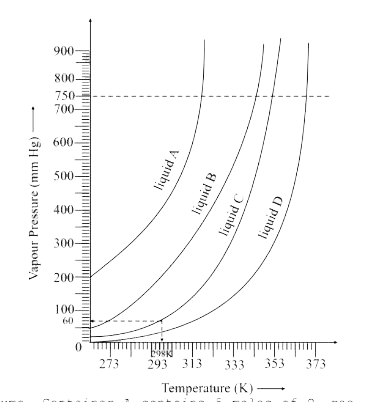
Calculate graphically boiling points of liquids A and B.
View SolutionTwo rods of different materials having coefficient of thermal expansion α1 and α2 and Young's moduli Y1 AND Y2 respectively are fixed between two rigid massive walls. The rods are heated such that they undergo the same increase in temperature. There is no bending of the rods. If α1 and α2 are in the ratio2:3, the thermal stresses i the rods would be same for ratio Y1/Y2=
View SolutionTwo rods of different materials having coefficients of thermal expansion α1,α2 and Young's Moduli Y1,Y2 respectively are fixed between two rigid massive walls. The rods are heated such that they undergo the same increase in temperature. There is no bending of the rods. If α1:α2=2:3, the thermal stresses developed in the two rods are equal provided Y1:Y2 is equal to
View SolutionTwo rods of different materials having coefficient of thermal expansion α1andα2 and Young's modulues Y1andY2 respectively are fixed betwee two rigid massive walls. The rods are heated such that these undergo same increase in temperature. there is no bending of the rods. if α1:α2=2:3, the thermal stress developed in the two rods are equal, provided Y1:Y2 is
View Solution
