A boy sitting on the top most berth in the compartment of a train which is just goint to stop on a railway station, drops an apple aiming at the open hand of his brother situated vertically below his hands at distance of about 2m. The apple will fall:-
In the hand of his brother
Slightly away from the hands of his brother in the direction of motion of the train
Slightly away from the hands of his brother in the direction opposite to the direction of motion of the train
None of the above
The correct Answer is:B
To solve the problem, we need to analyze the motion of the apple dropped by the boy in the train. Here’s a step-by-step breakdown:
Step 1: Understand the Situation
The boy is sitting in a train that is decelerating (retarding) as it approaches a station. He drops an apple aiming for his brother's hand, which is directly below him at a distance of 2 meters.
Hint: Consider the effects of the train's deceleration on the motion of the apple.
Step 2: Analyze the Forces Acting on the Apple
When the boy drops the apple, it is initially moving with the same horizontal velocity as the train. However, as the train is decelerating, the apple will continue to move forward due to inertia (Newton's first law of motion).
Hint: Remember that the apple has an initial horizontal velocity equal to that of the train.
Step 3: Determine the Motion of the Apple
As the apple falls, it will not only fall vertically due to gravity but will also continue to move horizontally in the direction of the train's initial motion. This results in a parabolic trajectory.
Hint: Think about how the horizontal and vertical motions are independent of each other.
Step 4: Calculate the Time of Fall
The time it takes for the apple to fall 2 meters can be calculated using the equation of motion under gravity:
h=12gt2
where h=2m and g≈9.81m/s2. Rearranging gives:
t=√2hg
Hint: Use the value of g to find the time of fall.
Step 5: Calculate the Horizontal Displacement
During the time t that the apple is falling, it will also move horizontally. The horizontal distance d can be calculated using:
d=vinitial⋅t
where vinitial is the initial horizontal velocity of the apple (same as the train's velocity).
Hint: Consider how far the apple travels horizontally during the time it is falling.
Step 6: Conclusion
Since the apple is moving forward while falling, it will land slightly away from the brother's hand in the direction of the train's motion. Therefore, the apple will not fall directly into the brother's hand.
Final Answer: The apple will fall slightly away from the brother's hand in the direction of the motion of the train.
The boy is sitting in a train that is decelerating (retarding) as it approaches a station. He drops an apple aiming for his brother's hand, which is directly below him at a distance of 2 meters.
When the boy drops the apple, it is initially moving with the same horizontal velocity as the train. However, as the train is decelerating, the apple will continue to move forward due to inertia (Newton's first law of motion).
As the apple falls, it will not only fall vertically due to gravity but will also continue to move horizontally in the direction of the train's initial motion. This results in a parabolic trajectory.
The time it takes for the apple to fall 2 meters can be calculated using the equation of motion under gravity:
h=12gt2
where h=2m and g≈9.81m/s2. Rearranging gives:
t=√2hg
During the time t that the apple is falling, it will also move horizontally. The horizontal distance d can be calculated using:
d=vinitial⋅t
where vinitial is the initial horizontal velocity of the apple (same as the train's velocity).
Since the apple is moving forward while falling, it will land slightly away from the brother's hand in the direction of the train's motion. Therefore, the apple will not fall directly into the brother's hand.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
Similar Questions
A boy sitting on the top most berth in the compartment of a train which is just going to stop on railway station, drops and apple aiming at the open hand of his brother situated vertically below his hands at a distance of about 2m. The apple will fail
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.

When the ball lands on the floor, the stop watch reads:
View Solution
Knowledge Check
A boy sitting on the topmost berth in the compartment of a train which is just going to stop on a railway station, drop an apple aiming at the open hand of his brother sitting vertically below his hands at a distnace of about 2 meter. The apple willl fall
APreciselt on the hand of his brotherBSlightly away from the hand of his brother in the direction of motion of the trainCSlightly away from the hand of his brother in the direction opposite of the direction of motion of the trainDNone of theseA man is sitting on the upper birth of the coach of a train, which is to be stopped on a nearby station. Man drops an apple on the open hand of his friend sitting just below the man about 2 m away. Apple will drop
Aexact in the hand of his friendBlittle away from the hand, in the direction of motion of trainsClittle away from the hand, opposite to the direction of motion of trainDNone of theseA man is sitting on the upper birth of the coach of a train, which is to be stopped on a nearby station. Man drops an apple on the open hand' of his friend, sitting just below the man about 2 m away. Apple will drop
Aexact in the hand of his friendBlittle away from the hand, in the direction of motion of trainsClittle away from the hand, opposite to the direction of motion of trainDNone of the above
Two rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
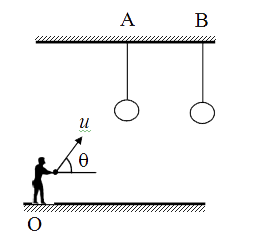
The ball lands on the floor at a distance:
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
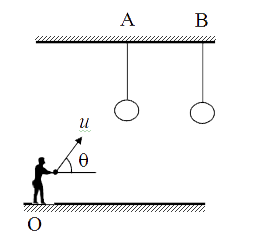
The projection speed of the ball is:
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
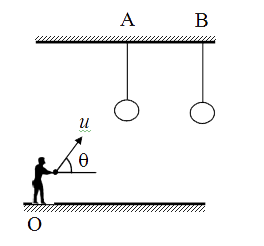
The maximum height attained by the ball above the floor is:
View SolutionTwo rings are suspended from the points A and B on the ceiling of a room with the help of strings of length 1.2 m each as shown. The points A and B are separated from each other by a distance AB = 1.2 m. A boy standing on the floor throws a small ball so that it passes through the two rings whose diameter is slightly greater than the ball. At the moment when the boy throws the ball, his hand is at a height of 1.0 m above the floor. A stop watch which is switched on at the moment of throwing the ball reads 0.2 s when the ball passes through the first ring and 0.6 s when it passes through the second ring.
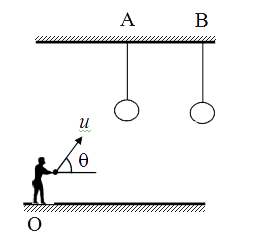
The angle of projection of the ball is:
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.
A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.
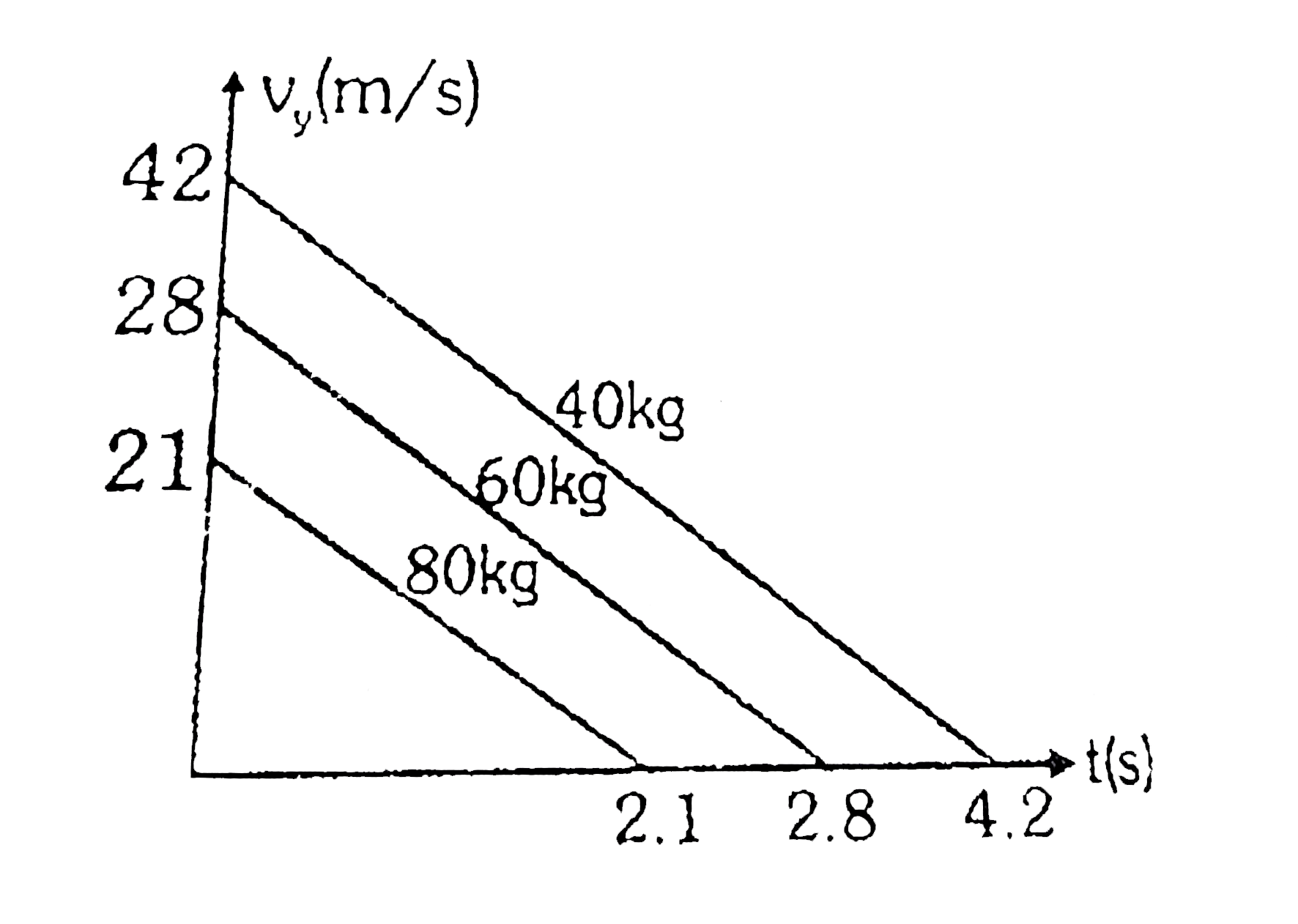
From figure 2, approximately how much time will it take for clown with a mass of 60 kg to reach the safety net located 10m below the height of the cannot?
View Solution
