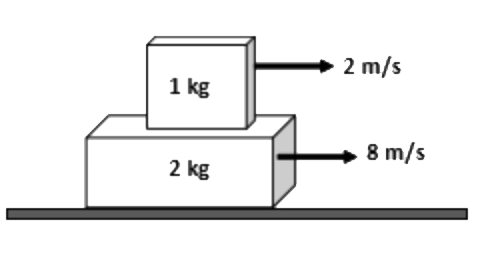
Coefficient of friction between two block shown in figure is μ=0.4. The blocks are given velocities of 2m/s and 8m/s in the directions figure. Find

(a) The time when relative motion between them will stop
(b) the common velocities of blocks upto that instant. (c) Displacement of 1kg and 2kg block upto that instant (g=10m/s2).
(i) Frictional force between two blocks will oppose the relative motion. For 1 kg block friction support themotion & for 2 kg friction oppose the motion. Let common velocity be v then
for 1kgv=2+a1t where a1=μ(1g)2=0.4×102=2ms−2⇒2+4t=8−2t⇒6t=5⇒t=1s
(ii) v=2+4t=2+4×1=6ms−1
(iii) Displacement of 1kg block from initial point s=ut+12at2⇒s1=2×1+12×4×12=2+2=4m
Displacement of 2kg block from intial point s=ut+12at2⇒s2=8×1−12×2×12=8−1=7m
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-I
52 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-II
112 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- RACEBOOK - ALLENCHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
Similar Questions
Coefficient of friction between two blocks shown in Fig. 7.203 is μ=0.4 . The blocks are given velocities of 2 m/s and 8 m/s in the directions shown in figure . The time when relative motion between them will stop is ( in sec) . :

View Solutioncoefficient of friction between two blocks shown in figure is μ=0.6. The blocks are given velocities in the direction shown in figure. Find
(a) the time when relative motion between them is slopped.
(b) the common velocity of the two blocks.
(c) the displocement of 1kg and 2kg blocks upto that instant. (Takeg=10m/s2)

View Solution
Knowledge Check
In the figure two blocks are given velocities as shown. The lower block is very long. Find velocities of both the blocks when relative motion between them is ceased
 A2m/s (towards right)B1m/s (towards left)C2m/s (towards left)D1m/s (towards right)
A2m/s (towards right)B1m/s (towards left)C2m/s (towards left)D1m/s (towards right)In the figure shown upper block is given a velocity of 6m/s and lower block 3m/s. When relative motion between them is stopped.
 .AWork done by friction on upper block is negativeBWork done by friction on both blocks is positiveCThe magnitude of work done by friction on upper block is 10JDNet work done by friction is zero.
.AWork done by friction on upper block is negativeBWork done by friction on both blocks is positiveCThe magnitude of work done by friction on upper block is 10JDNet work done by friction is zero.In the figure shown, upper block is given a velocity of 6m/s and lower block. 3m/s. When relative motion between them is stopped
 AWork done by friction on upper block is −10JBWork done by friction on lower block +10JCNet work done by friction is zeroDAll of the above
AWork done by friction on upper block is −10JBWork done by friction on lower block +10JCNet work done by friction is zeroDAll of the above
A conveyor belt is moving with constant speed of 6m/s. A small block is just dropped on it.Coefficient of friction between the two is μ=0.3. Find

(a) The time when relative motion between them will stop
(b) Displacement of block upto that instant (g=10m/s2).
View SolutionThe coefficient of friction between the two blocks shown in the figure is μ=0.4 and between the lower block and the ground is zero. The blocks are given velocities of 2ms−1 and 8ms−1 respectively in the direction shown in the figure. In how much time (in seconds) the slipping between the blocks will stops ?
View SolutionIn the figure shown, upper block is given a velocity of 6m/s and lower block. 3m/s. When relative motion between them is stopped

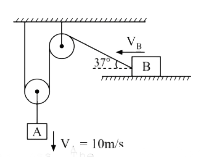
View SolutionIn the arrangement shown, velocity of block A is 10 m/s at a moment. Then the velocity of block B at this instant is :
View SolutionTwo blocks of masses 2m and m are in equilibrium a shown in the figure. Now the string between the blocks is suddenly broken. The accelarations of the blocks A and B respectively, at that instant are

View Solution
