For particle in SHM, the displacement x of the particle as a function o time t is given as x=Asin(2πt). Here x is in cm and t is in second. Let the time taken by the particle to travel from x=0 to x=A2 be t1 and the time taken to travel from x=A2 to x=A be t2 find t1t2Solution in Tamil
Here x=0 at t=0
Also ω=2πT=2π, ∴T=1s
At t=t1,x=A2
A2=Asin(2πt1)
(or) 12=sin(2πt1)
∴2πt1=π6(or)t1=112s
Time taken from x =0 to x=A is T4=14s
(or) t1+t2=T2=14s
Hence t1t2=1/121/6=12
Topper's Solved these Questions
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( CONCEPTUAL QUESTIONS.)
24 Videos
- OSCILLATIONS BOOK - PREMIERS PUBLISHERSCHAPTER - OSCILLATIONS EXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS ( LONG ANSWER QUESTIONS )
12 Videos
- NATURE OF PHYSICAL WORLD AND MEASUREMENTBOOK - PREMIERS PUBLISHERSCHAPTER - NATURE OF PHYSICAL WORLD AND MEASUREMENTEXERCISE - OTHER IMPORTANT QUESTIONS & ANSWERS (III. Short Answer Questions.)
24 Videos
- PROPERTIES OF MATTERBOOK - PREMIERS PUBLISHERSCHAPTER - PROPERTIES OF MATTEREXERCISE - OTHER IMPORTANT QUESTION & ANSWERS (NUMERICAL PROBLEMS)
56 Videos
Similar Questions
Can a motion be periodic and not oscillatory ?
View SolutionDerive expressions for displacement, velocity and acceleration of a particle executing simple harmonic motion.
View SolutionWhat is meant by Parallax?
View SolutionA material breaks up under a stress of 20×105N/m2. If the density of the material is 2.5×103kg/m3, calculate the length may break under its own weight.(Take g=10m/s2)
View Solutionx−t graph of a particle in SHM is
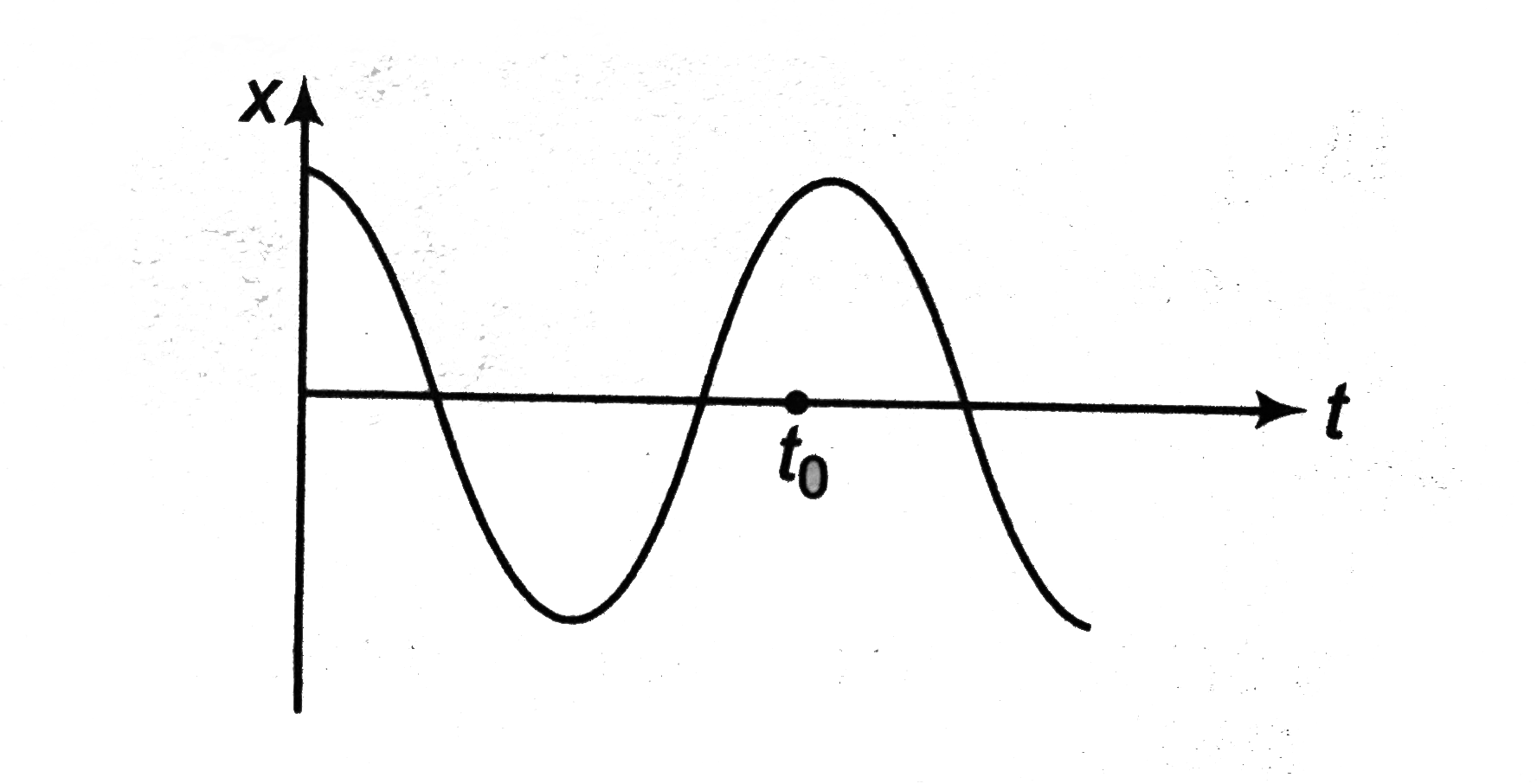
At time t=t0, what are the signs of v and a of the particle?
View SolutionA particle executes SHM in accordance with x=A"sin"omegat . If t_(1) is the time taken by it to reach from x=0 to x=sqrt(3)(A//2) and t_(2) is the time taken by it to reach from x=sqrt(3)//2 A to x=A , the value of t_(1)//t_(2) is
View SolutionFind the time taken by the particle in going from = x = (A)/2) to x=A Hint : t_(1) = Time taken to go from x=0 to x =A t_(2) = Time taken to go from x=0 to x= (A)/(2) Required time = t_(1) - t_(2)
View SolutionA particle startsits SHM at t=0 . At a particular instant on its way to extreme position , x= (A)/(2) . Find the time taken by the particle to come back to this point after passing through the extreme position. Hint : t_(1) = time taken to go from x=0 to x= (A)/(2) t_(2) = time taken to go to extreme position and come back to mean position = (T)/(2) Required time = (T)/(2) - t_(1)
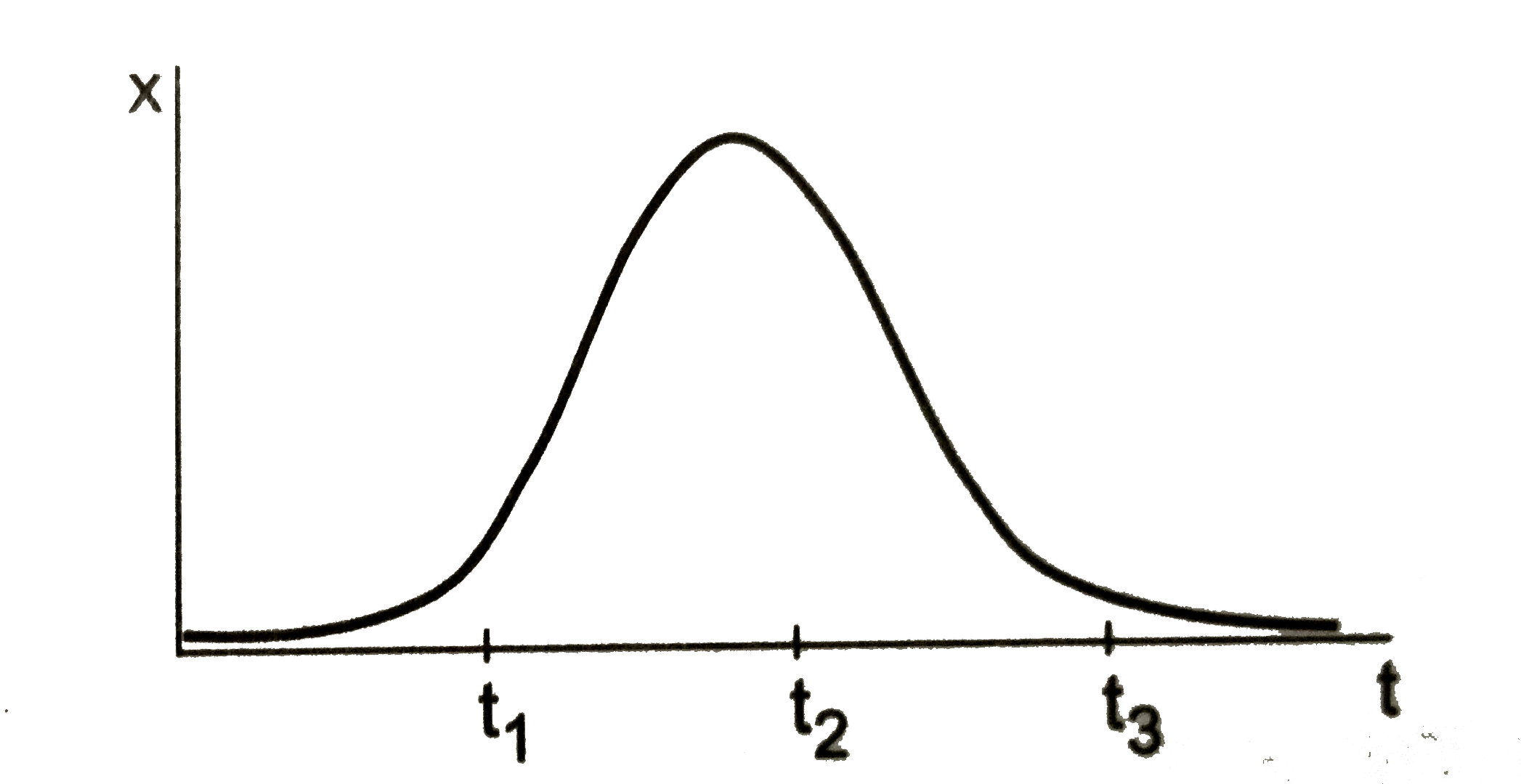
View Solutionचित्र में एक कण के x -निर्देशांक का समय के साथ संबंध बताया गया है । vxतथा ax के चिह्न t=t1,t=t2एवं t=t3 पर क्या होंगे ?
View Solutionएक कण x=Asinωt के अनुसार सरल आवर्त गति कर रहा है | यदि कण को x = 0 से x=√3A/2 तक पहुँचने में समय t1 तथा x=√3A/2 से x=A तक पहुँचने में समय t2 लगता है तो t1/t2 का मान होगा :
View SolutionFor particle in SHM, the displacement x of the particle as a function o time t is given as x=A sin (2pi t) . Here x is in cm and t is in second. Let the time taken by the particle to travel from x=0 to x=(A)/(2) be t_(1) and the time taken to travel from x=(A)/(2) to x=A be t_(2) find (t_(1))/(t_(2))
View SolutionThe displacement of a particle undergoing S.H.M. as a function of time t is given by
x=Asin(4πt3)
Where x is in cm and t in second
The time taken by the particle to travel from (a) x = 0 to A/2 is ta and time taken by it to travel from (b) x = A/2 to A is tb. Calculate the ratio tb/ta.
View SolutionA particle executes SHM of type x=Asinωt. It takes time t1 from x=0 to x=A2andt2 from x=A2 to x=A. The ratio t1:t2 will be
View Solutionx=a sin omega t Of x = 0 to a particle with simple periodic motion of x=(a)/(2) Time taken to migrate t_(1) , And x=(a)/(2) Time taken to migrate from x = a t_(2) If so t_(1) : t_(2) Will happen :
View SolutionA particle encute SHM between x = -A and x = +A , The time taken for it to go from 0 to A//2 is T_(1) and to go from A//2 to A is T_(2) , then
View Solution
