The displacement of a particle undergoing S.H.M. as a function of time t is given by
x=Asin(4πt3)
Where x is in cm and t in second
The time taken by the particle to travel from (a) x = 0 to A/2 is ta and time taken by it to travel from (b) x = A/2 to A is tb. Calculate the ratio tb/ta.
To solve the problem, we need to find the ratio of the time taken by a particle undergoing simple harmonic motion (SHM) to travel from x=0 to x=A2 (denoted as ta) and from x=A2 to x=A (denoted as tb).
1. Identify the equation of motion:
The displacement of the particle is given by:
x=Asin(4πt3)
Here, A is the amplitude and ω=4π3 is the angular frequency.
2. Find the time ta to travel from x=0 to x=A2:
- At x=0:
0=Asin(4πta3)⟹sin(4πta3)=0
This occurs when:
4πta3=nπ(n=0,1,2,…)
For n=0, ta=0. For n=1:
ta=34
- At x=A2:
A2=Asin(4πta3)⟹sin(4πta3)=12
This occurs when:
4πta3=π6or4πta3=5π6
Solving for ta:
- For 4πta3=π6:
ta=324=18 seconds
- For 4πta3=5π6:
ta=1524=58 seconds
Thus, the time taken ta is 18 seconds.
3. Find the time tb to travel from x=A2 to x=A:
- At x=A:
A=Asin(4πtb3)⟹sin(4πtb3)=1
This occurs when:
4πtb3=π2
Solving for tb:
tb=38 seconds
4. Calculate the ratio tbta:
tbta=3818=3
Final Answer:
The ratio tbta is 3.
The displacement of the particle is given by:
x=Asin(4πt3)
Here, A is the amplitude and ω=4π3 is the angular frequency.
- At x=0:
0=Asin(4πta3)⟹sin(4πta3)=0
This occurs when:
4πta3=nπ(n=0,1,2,…)
For n=0, ta=0. For n=1:
ta=34
A2=Asin(4πta3)⟹sin(4πta3)=12
This occurs when:
4πta3=π6or4πta3=5π6
Solving for ta:
- For 4πta3=π6:
ta=324=18 seconds
- For 4πta3=5π6:
ta=1524=58 seconds
Thus, the time taken ta is 18 seconds.
- At x=A:
A=Asin(4πtb3)⟹sin(4πtb3)=1
This occurs when:
4πtb3=π2
Solving for tb:
tb=38 seconds
tbta=3818=3
The ratio tbta is 3.
Topper's Solved these Questions
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS15videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - OSCILLATIONS EXERCISE - PRACTICE PROBLEMS 220videos
OSCILLATIONS
- BOOK - MODERN PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - CHAPTER PRACTICE TEST16videos
MOTION IN A STRAIGHT LINE
- BOOK - MODERN PUBLICATIONCHAPTER - PHYSICAL WORLD EXERCISE - Revision exercises (Long answer questions)6videos
PHYSICAL WORLD
Similar Questions
The x and y coordinates of a particle at any time t are given by x=2t+4t2andy=5t , where x and y are in metre and t in second. The acceleration of the particle at t = 5 s is
View SolutionThe x and y coordinates of a particle at any time t is given by x=7t+4t2 and y=5t, where x and y are in metre and t in seconds. The acceleration of particle at t=5s is
View Solution
Knowledge Check
- Question 1 - Select One
The displacement of a particle performing a S.H.M. is given by x=0.5sin100π(t+0.05), where x is in metres and t is in second. Its periodic time in second is
A0.01sB0.02sC0.1sD0.5s - Question 2 - Select One
The displacement of a particle of a string carrying a travelling wave is given by y=(4cm)sin2π(0.5x−100t), where x is in cm and t is in seconds. The speed of the wave is
A50 cm/sB100 cm/sC200 cm/sD250 cm/s - Question 3 - Select One
Time taken by the particle to reach from A to B is t. Then the distance AB is equal to
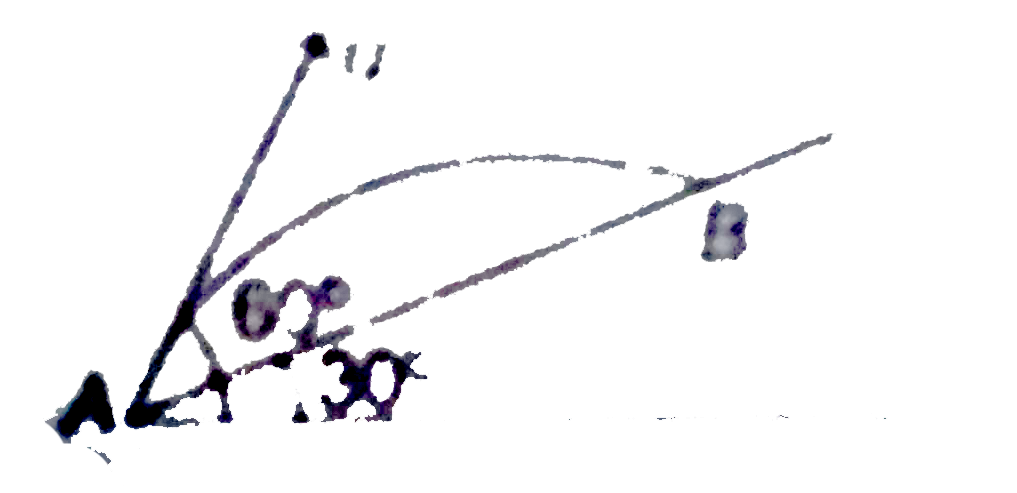 Aut√3B√3ut2C√3utD2ut
Aut√3B√3ut2C√3utD2ut
The displacemeent of a particle is given at time t by x=Asin(−2ωt)+Bsin2ωt. Then,
View SolutionThe displacement of a particle executing SHM at any time t (Seconds) is x=0.01sin100π(t=0.005) then its time period will be
View SolutionThe velocity v of a particle at any instant t moving in a straight line is given by v=s +1 where s meter is the distance travelled in t second what is the time taken by the particle to cover a distacne of 9m ?
View SolutionThe displacement of a particle is given at time t, by:
x=Asin(−2ωt)+Bsin2ωt Then,View Solutionx and y co-ordinates of a particle moving in x−y plane at some instant of time are x=2t and y=4t.Here x and y are in metre and t in second. Then
The distance travelled by the particle in a time from t=0 to t=2s is ………mView Solution
