Euclid's division lemma states that for positive integers a and b, there exist unique integers q and r such that a=bq+r, where r must satisfy.Solution in Tamil
1<r<b
0<r<b
0≤r<b
0<r≤b
The correct Answer is:C
Step by step video, text & image solution for Euclid's division lemma states that for positive integers a and b, there exist unique integers q and r such that a=bq+r, where r must satisfy. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - UNIT EXERCISE12videos
NUMBERS AND SEQUENCES
- BOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - THINKING CORNER13videos
NUMBERS AND SEQUENCES
- BOOK - PREMIERS PUBLISHERSCHAPTER - NUMBERS AND SEQUENCESEXERCISE - EXERCISE 2. 914videos
NUMBERS AND SEQUENCES
- BOOK - PREMIERS PUBLISHERSCHAPTER - MENSURATIONEXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS16videos
MENSURATION
- BOOK - PREMIERS PUBLISHERSCHAPTER - RELATIONS AND FUNCTION EXERCISE - OTHER IMPORTANT OBJECTIVE TYPE QUESTIONS25videos
RELATIONS AND FUNCTION
Similar Questions
Prove that n2−n divisible by 2 for every positive integer n.
04:15View SolutionWhen a positive integer is divided by 3
What are the possible remainders?01:13View SolutionFind the sum of the following series
1+2+3+…+6002:18View SolutionMatch the following:
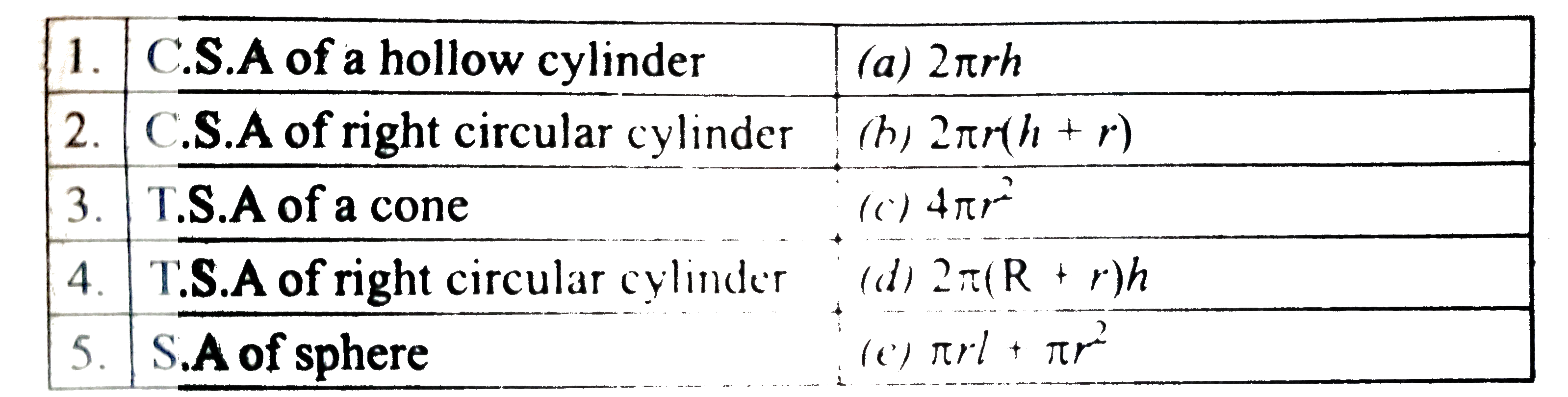
06:23View SolutionIf n(A×B)=24andA={1,3,5,7}then n (B) is
03:42View SolutionProve that if a and b are integers with b>0, then there exist unique integers q and r satisfying a=qb+r, where 2b<=r<3b
02:25View Solutionकिन्ही धनात्मक पूर्णाको q और r के लिए अद्वितीय पूर्णांक q और r इस प्रकार विघमान होते है कि aa = b + r जहाँ r संतुष्ट करेगा
01:12View Solutionयूक्लिड प्रमेयिका के अनुसार धनात्मक पूर्णांक a व b के लिए अद्वितीय पूर्णांक q व r का अस्तित्व इस प्रकार है कि a = bq + r, तब r द्वारा संतुष्ट असमिका ज्ञात कीजिए ।
01:36View SolutionTheorem 1.1 (Euclid’s Division Lemma) : Given positive integers a and b, there exist unique integers q and r satisfying a = bq + r, 0 ≤ r ≤ b.
01:29View Solutionयूक्लिड की विभाजन युप्रमेय के अनुशार किन्ही दो धनात्मक संख्याओं a तथा b के संगत दो अद्वितीय पूर्णांक q तथा r इस प्रकार होते है की a=bq+r, जहाँ r निम्न में से किसको संतुस्ट करता है
View SolutionEuclid's division lemma states that for positive integers a and b, there exist unique integers q and r such that a=bq+r, where r must satisfy.
02:56View Solution.For any positive integera and 3,there exist unique integers q and r such that a=3q+r where r must satisfy:
01:15View SolutionEuclid's division Lemma states that for two positive integers a and b, there exist unique integers q and r such that a=bq+r where r must satisfy.
02:39View SolutionEuclids Division Lemma states that for any two positive integers a and b, there exists unique integers q and r such that a=bq+r, where r must satisfy.
02:34View SolutionBy Euclid division lemma ,for given positive integers a and b , there exist unique integers q and r satisfying a = bq + r then r is
03:42View SolutionTheorem 1.1 (Euclid’s Division Lemma) : Given positive integers a and b, there exist unique integers q and r satisfying a = bq + r, 0 ≤ r ≤ b.
02:14View Solution