In AB and CD are two equal chords of a circle with center O. OP and OQ are perpendiculars on chords AB and CD respectively. If ∠POQ=150∘ then ∠APQ is equal to
30∘
75∘
15∘
60∘
The correct Answer is:B
To solve the problem step by step, we will follow the reasoning laid out in the video transcript and break it down into clear steps.
1. Understanding the Given Information:
- We have two equal chords AB and CD in a circle with center O.
- OP and OQ are perpendiculars drawn from the center O to the chords AB and CD, respectively.
- We are given that ∠POQ=150∘.
2. Identifying Equal Distances:
- Since AB and CD are equal chords, the perpendicular distances from the center O to these chords are also equal. Therefore, OP=OQ.
3. Setting Up Angles:
- Let ∠BOP=∠AOP=θ (angles formed by the radius and the perpendicular).
- Since OP and OQ are equal, the triangles formed (triangle OAP and triangle OBP) are isosceles triangles. Thus, ∠APQ=∠BQP.
4. Using the Triangle Angle Sum Property:
- In triangle POQ, the sum of the angles is 180∘:
∠POQ+∠OPQ+∠OQP=180∘
- Since ∠POQ=150∘, we have:
150∘+∠OPQ+∠OQP=180∘
- This simplifies to:
∠OPQ+∠OQP=30∘
5. Finding Each Angle:
- Since ∠OPQ=∠OQP (because they are angles opposite to equal sides in triangle OPQ), we can let:
∠OPQ=∠OQP=x
- Thus, we have:
2x=30∘⟹x=15∘
- Therefore, ∠OPQ=15∘ and ∠OQP=15∘.
6. Finding Angle APQ:
- Now consider the straight line AB:
∠BPO+∠APQ+∠OPB=180∘
- Since ∠BPO=90∘ (because OP is perpendicular to AB), we have:
90∘+∠APQ+15∘=180∘
- This simplifies to:
∠APQ=180∘−105∘=75∘
Final Answer:
The measure of ∠APQ is 75∘.
---
- We have two equal chords AB and CD in a circle with center O.
- OP and OQ are perpendiculars drawn from the center O to the chords AB and CD, respectively.
- We are given that ∠POQ=150∘.
- Since AB and CD are equal chords, the perpendicular distances from the center O to these chords are also equal. Therefore, OP=OQ.
- Let ∠BOP=∠AOP=θ (angles formed by the radius and the perpendicular).
- Since OP and OQ are equal, the triangles formed (triangle OAP and triangle OBP) are isosceles triangles. Thus, ∠APQ=∠BQP.
- In triangle POQ, the sum of the angles is 180∘:
∠POQ+∠OPQ+∠OQP=180∘
- Since ∠POQ=150∘, we have:
150∘+∠OPQ+∠OQP=180∘
- This simplifies to:
∠OPQ+∠OQP=30∘
- Since ∠OPQ=∠OQP (because they are angles opposite to equal sides in triangle OPQ), we can let:
∠OPQ=∠OQP=x
- Thus, we have:
2x=30∘⟹x=15∘
- Therefore, ∠OPQ=15∘ and ∠OQP=15∘.
- Now consider the straight line AB:
∠BPO+∠APQ+∠OPB=180∘
- Since ∠BPO=90∘ (because OP is perpendicular to AB), we have:
90∘+∠APQ+15∘=180∘
- This simplifies to:
∠APQ=180∘−105∘=75∘
The measure of ∠APQ is 75∘.
Topper's Solved these Questions
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PART-A (Fill in the Blanks)
3 Videos
- CIRCLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CIRCLESEXERCISE - PART-A (TRUE/FALSE)
13 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLESBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLESEXERCISE - PRACTICE TEST
2 Videos
- CO-ORDINATE GEOMETRYBOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - PRACTICE TEST
9 Videos
Similar Questions
Knowledge Check
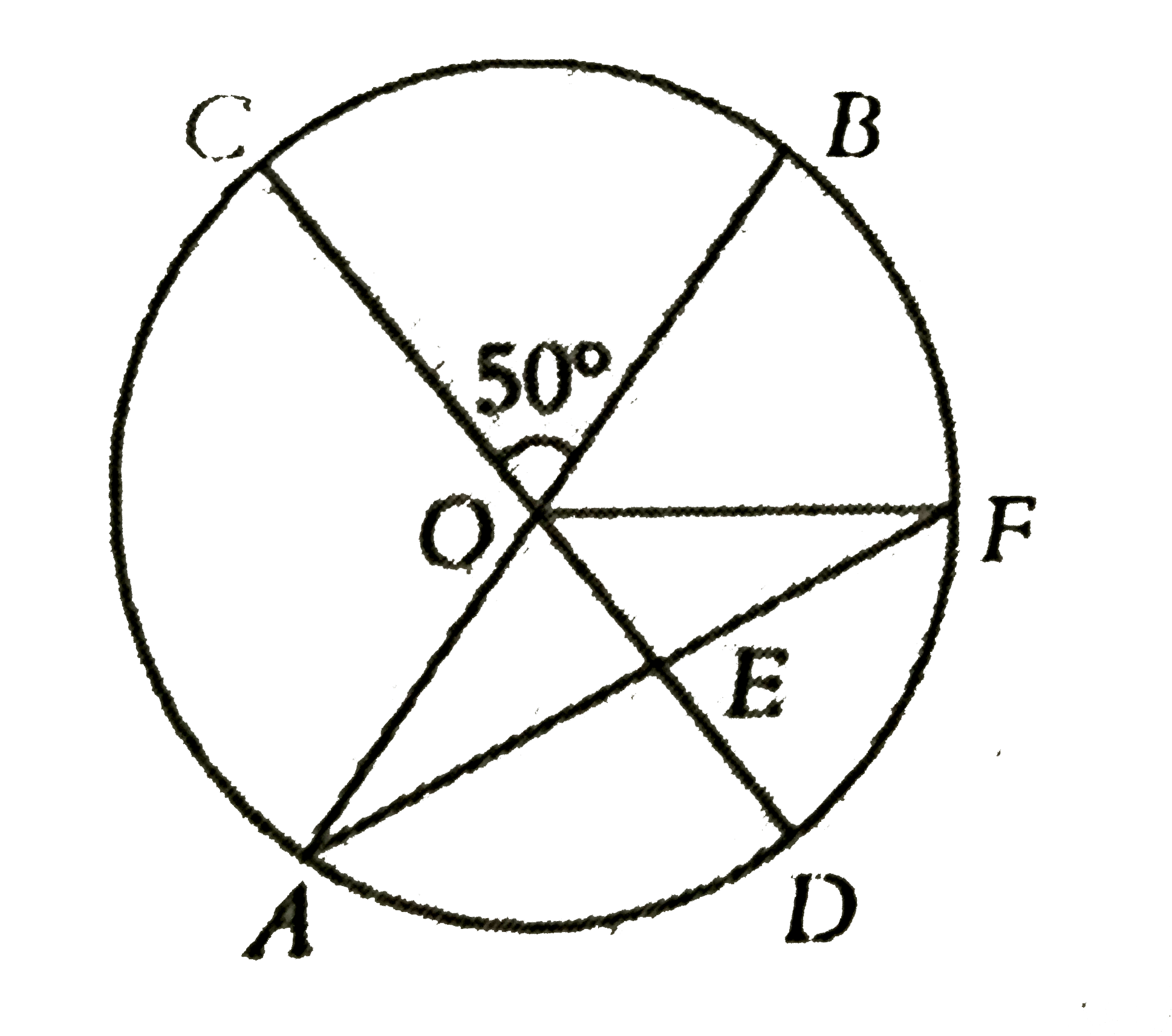
In the above figure , O is the centre of the circle, AB and CD are diameters. ∠COB=50∘=50∘ . If E is the midpoint of AF, then find ∠ADFA65∘B55∘C70∘D50∘Let AB and CD are two parallel chords of circle whose radius is 5 units. If P and Q are mid points of AB and CD respectively such that PA. PB = 9, QC. QD = 16, then distance between AB and CD is
A5B25C7D11Let AB and CD are two parallel
chords of circle whose radius is
5 units. If P and Q are mid points
of AB and CD respectively such that
P.A.PB=9,QC.QD=16,
then distance between AB and CD isA5B25C7D11
AB and CD are two parallel chords of a circle whose diameter is AC . Prove that AB=CD.
View SolutionAB and CD are two parallel chords of a circle whose diameter is AC . Prove that AB=CD
View SolutionABandCD are equal chords of a circle whose centre is O, when produced these chords meet at E,Prove that EB=ED.
View SolutionAB and CD are equal and parallel chords of a circle with centre O. Then AC passes through the centre O. [Agree / Disagree]
View SolutionIn the given figure,AB and CDare equal chords of a circle with centre O .Prove that ∠AOB≅∠COD and ∠AOB=∠COD
View Solution
