When light travels from glass to air, the incident angle is θ1 and the refracted angle is θ2. The true relation is
θ1=θ2
θ1<θ2
θ1≥θ2
Not predictable
The correct Answer is:2
Step by step video & text solution for When light travels from glass to air, the incident angle is theta_(1) and the refracted angle is theta_(2). The true relation is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A ray of light is travelling from glass to air. The angle of incidence in glass is 35∘, and angle of refraction in air 60∘. What is the refractive index of glass w.r.t. air ? [sin35∘=(0.5736)]
A1.9B0.5C1.51D2.0A ray of light is travelling from glass to air. (Refractive index of glass =1.5). The angle of incidence is 50∘. The deviation of the ray is
A0∘B80∘C50∘−sin−1[sin50∘1.5]Dsin−1[sin506∘1.5]−50∘A ray of light travelling from glass to air is incident at 50∘ from the glass air boundary . What is the angle of deviation if the critical angle is 42∘ ?
A0∘B60∘C80∘Dsin−1[sin50∘1.5]−50
A converging beam of light is incident on a right angled isosceles prism as shown in the Figure. The marginal rays in the beam are incident at angle ±θ. The refractive index for the glass of the prism is μ=1.49(=1sin42°) . Find the maximum value of θ for which no light comes out of the hypotenuse surface.
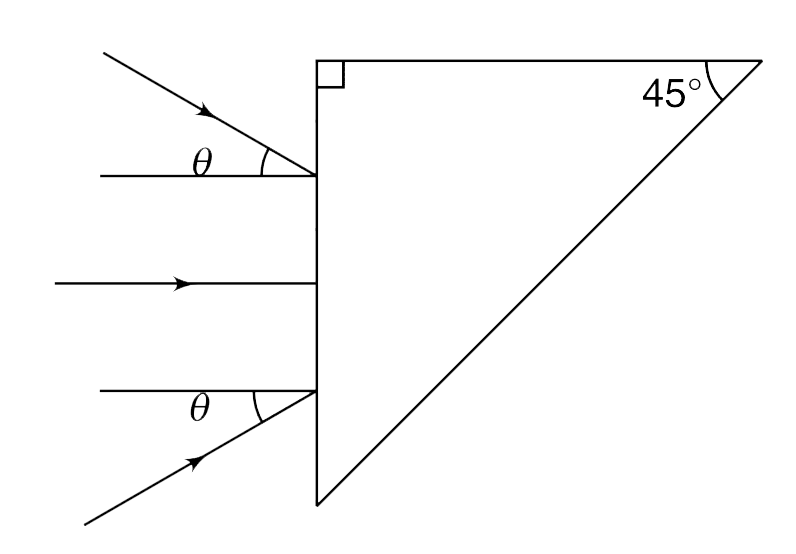
View SolutionA ray of light travels from air to glass. It is found that the angle of refraction is half the angle of incidence. The the angle of incidence is given by
View SolutionA ray of light travels from air to glass . It is found that the angle of refraction is half the angle of incidence . Then the angle of refraction is given by
View SolutionA light ray travelling in glass medium is incident of glass- air interface at an angle of incidence θ. The reflected (R) and transmitted (T) intensities, both as function of θ, are plotted The correct sketch is
View SolutionA ray of light traveling in glass (μ=3/2) is incident on a horizontal glass-air surface at the critical angle θC. If a thin layer of water (μ=4/3) is now poured on the glass-air surfac, the angle at which the ray emerges into air at the water-air surface is
View Solution
