_S01_026_Q01.png)
In a YDSE experiment two slits S1 and S2 have separation of d=2mm the distance of the screen is D=85 m source S starts moving from a very large distance towards S2 perpendicular to S1S2 as shown in figure the wavelength of monochromatic light is 500 n. The number of maximas observed on the screen at point P as the moves towards S2 is
4001
3999
3998
4000
The correct Answer is:4
S1O−S2P=d22D=2×10−3×2×10−32×8552λ(λ=500nm)
So when S is at ∞ there is Ist minima and when S is at S2 there is last minima because dλ=4000
So the number of minima.s will be 4001 and number of maxima.s will be 4000.
Similar Questions
In an interference experiment, the two slits S1andS2 are not equidistant from the source S. then the central fringe at 0 will be
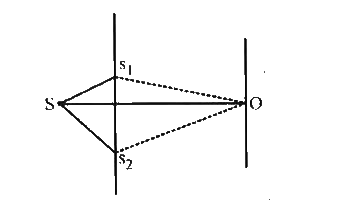
View SolutionTwo coherent point sources S1 and S2 vibrating in phase emit light of wavelength λ. The separation between the sources is 2λ. Consider a line passing through S1 and perpendicular to line S1S2. Find the position of farthest and nearest minima.
 .
.
View Solution
Knowledge Check
In the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
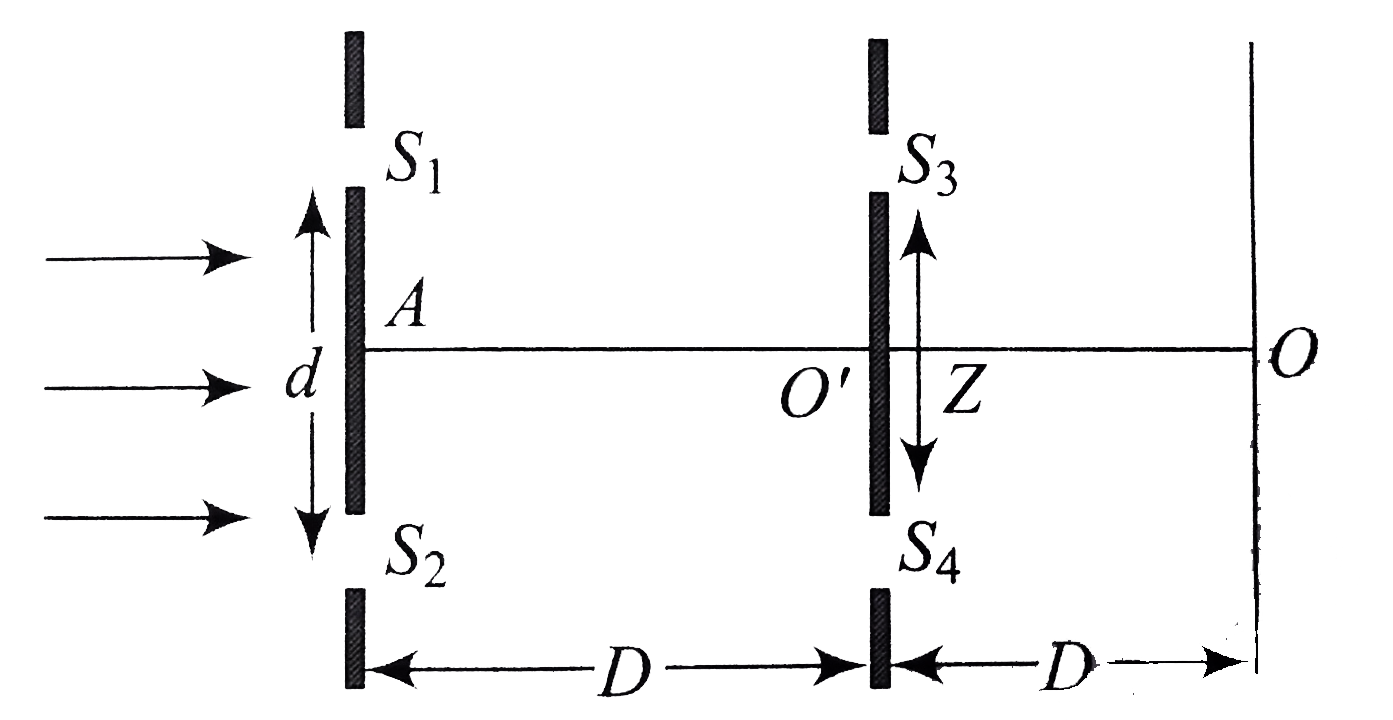
If a hole is made at O' on AO' O and the slit S4 is closed, then the ratio of the maximum to minimum observed on screen at O , if O'S3 is equal to λD4d, isA1BinfinityC34D4Two coherent point sources S1 and S2 are separated by a small distance d as shown. The fringes obtained on the screen will be
 ApointsBstraight linesCsemi-circlesDconcentric circles
ApointsBstraight linesCsemi-circlesDconcentric circlesIn a Young's double-slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is wavelength, the fringe width will be
AλθBλθC2λθDλ2θ
Two coherent point sources S1andS2 are separated by a small distance 'd' as shown. The fringes obtained on the screen will be :

View SolutionIn a Young's double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is the wavelength, the fringe width will be
View SolutionIn the arrangement shown in Fig., slits S1 and S4are having a variable separation Z. Point O on the screen is at the common perpendicular bisector of S1S2 and S3S4.
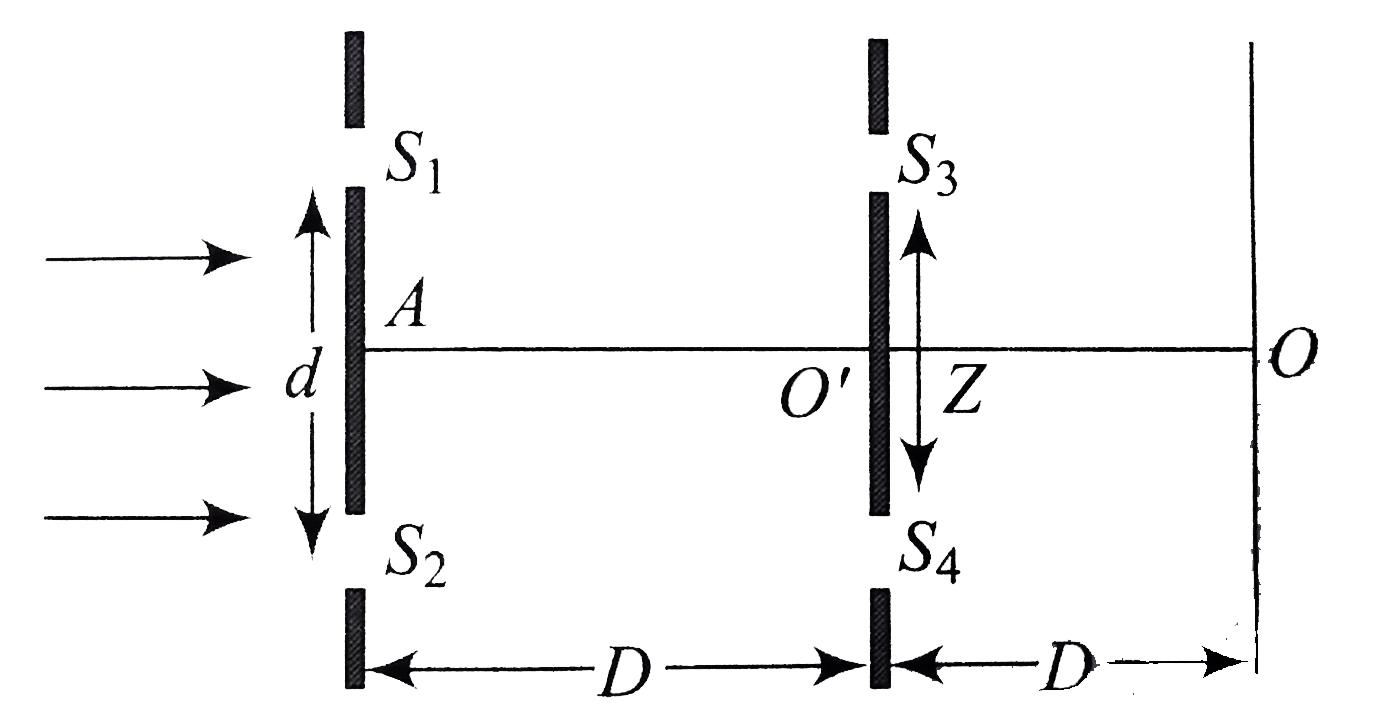
The minimum value of Z for which the intensity at O is zero is
View SolutionIn a Young's double slit experiment, the slit separation is 1mm and the screen is 1m from the slit. For a monochromatic light of wavelength 500nm, the distance of 3rd minima from the central maxima is
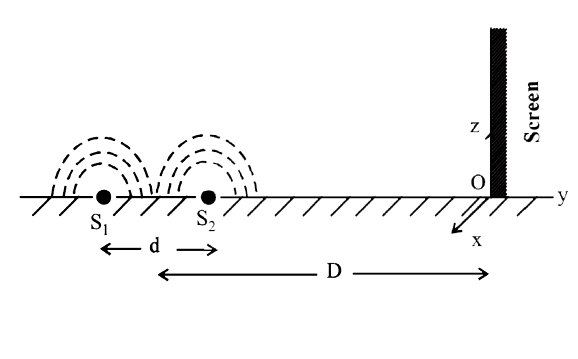
View SolutionWhile conduction the Young's double slit experiment, a student replaced the two slits with a large opaque plate in the x-y plane containing two small holes that act as two coherent point sources (S1,S2) emitting light of wavelength 600nm. The student mistakenly placed the screen parallel to the x-z plane (forz>0) at a distance D=3 m from the mid-point of S1,S2, as shown schematically in the figure. The distance between the sources d=0.6003mm. The origin O is at the intersection of the screen and the line joining S1S2. Which of the following is (are) true of the intensity pattern of the screen?
View Solution