In a metre bridge the null point is found at a distance of 35 cm from A. If now a resistance of 10Ω is connected in parallel with S, the null point occurs at 50 cm. Determine the values of R and S.
To solve the problem, we will use the principles of a meter bridge and the concept of resistances in parallel. Let's break it down step by step.
Step 1: Understand the Initial Condition
In the first scenario, the null point is found at a distance of 35 cm from point A. This means that the lengths on the meter bridge are:
- Length L1 = 35 cm
- Length L2 = 100 cm - L1 = 100 cm - 35 cm = 65 cm
According to the meter bridge principle, we have:
RS=L1L2=3565
This simplifies to:
RS=713(Equation 1)
Step 2: Understand the Condition with Parallel Resistance
Now, when a resistance of 10 Ω is connected in parallel with S, the new null point occurs at 50 cm from A. Thus, we have:
- New Length L' = 50 cm
- New Length L'' = 100 cm - L' = 100 cm - 50 cm = 50 cm
Using the meter bridge principle again, we have:
RSeq=L′L′′=5050=1
This implies:
R=Seq(Equation 2)
Step 3: Calculate the Equivalent Resistance
The equivalent resistance Seq when 10 Ω is connected in parallel with S is given by:
Seq=10⋅S10+S
Step 4: Substitute and Solve
From Equation 2, we have:
R=10⋅S10+S
Now we can substitute R from Equation 1 into this equation:
713S=10⋅S10+S
Step 5: Cross Multiply and Simplify
Cross multiplying gives us:
7(10+S)=130
Expanding this:
70+7S=130
Rearranging gives:
7S=130−70
7S=60
S=607Ω
Step 6: Find R Using S
Now, substitute S back into Equation 1 to find R:
R=713⋅607=6013Ω
Final Values
Thus, the values of R and S are:
R=6013ΩandS=607Ω
In the first scenario, the null point is found at a distance of 35 cm from point A. This means that the lengths on the meter bridge are:
- Length L1 = 35 cm
- Length L2 = 100 cm - L1 = 100 cm - 35 cm = 65 cm
RS=L1L2=3565
This simplifies to:
RS=713(Equation 1)
Now, when a resistance of 10 Ω is connected in parallel with S, the new null point occurs at 50 cm from A. Thus, we have:
- New Length L' = 50 cm
- New Length L'' = 100 cm - L' = 100 cm - 50 cm = 50 cm
RSeq=L′L′′=5050=1
This implies:
R=Seq(Equation 2)
The equivalent resistance Seq when 10 Ω is connected in parallel with S is given by:
Seq=10⋅S10+S
From Equation 2, we have:
R=10⋅S10+S
Now we can substitute R from Equation 1 into this equation:
713S=10⋅S10+S
Cross multiplying gives us:
7(10+S)=130
Expanding this:
70+7S=130
Rearranging gives:
7S=130−70
7S=60
S=607Ω
Now, substitute S back into Equation 1 to find R:
R=713⋅607=6013Ω
Thus, the values of R and S are:
R=6013ΩandS=607Ω
Similar Questions
In a meter bridge,
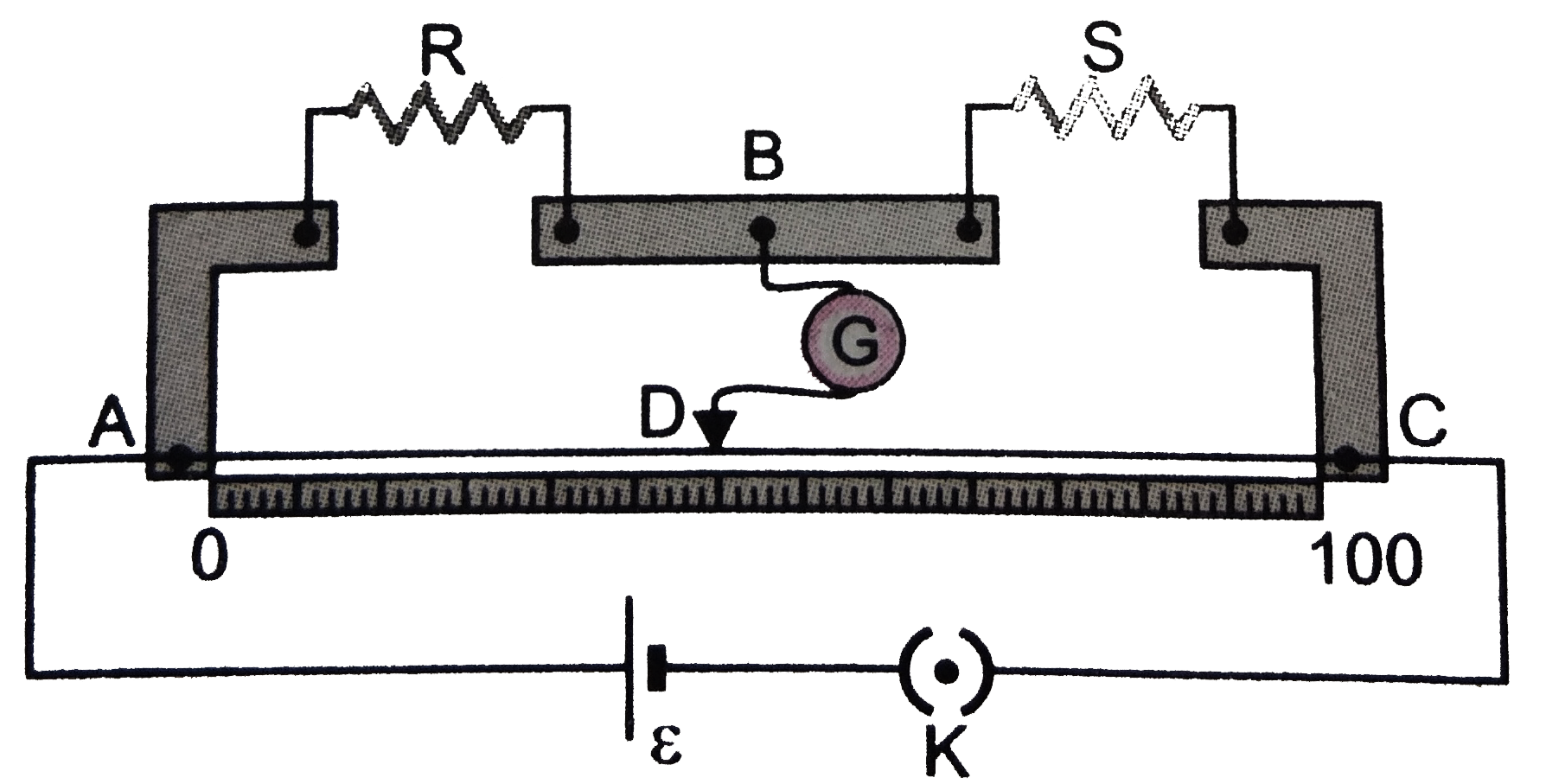
the null points is found at a distance of 33.7 cm from A. If now a resistance of 12Ω is connected in parallel with S, the null point occurs at 51.9 cm. Determine the values of R and S.
View SolutionIn a metre bridge the null point is found at a distance of 60.0 cm from A. If now a resistance of 5Ω is connected in series with S, the null point occurs at 50 cm. Determine the values of R and S.

View Solution
Knowledge Check
In a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 Ω is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.
 A15ΩB12ΩC10ΩD5Ω
A15ΩB12ΩC10ΩD5Ω
In a meter bridge, the null point is found at a distance of 40cm from A. If a resistance of 12Ω in connected in parallel with S the null point occurs at 50.0cm from A Determine the value of R and S

View SolutionIn meter bridge, the null points is found at a distance of 60.0 cm front end A. If now a resistance of 5Ω is connected in series with S, the null point occurs at 50 cm. Determine the values of R and S,
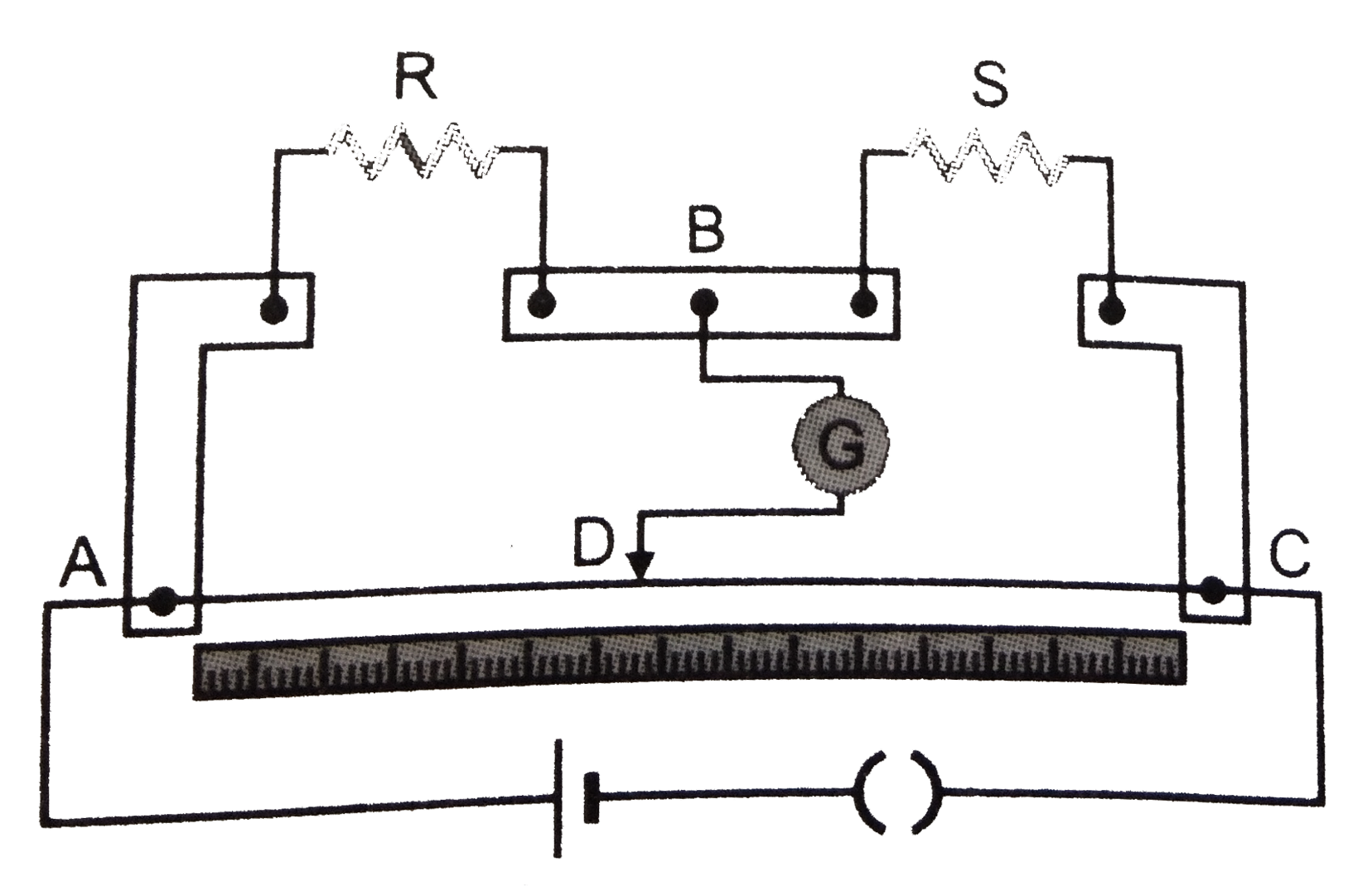
View SolutionCircuit diagram of metre bridge is shown in figure. The null point is found at a distance of 40cm from A. it now a resistance of 12Ω is connected in parallel with S, the null point occurs at 64cm.

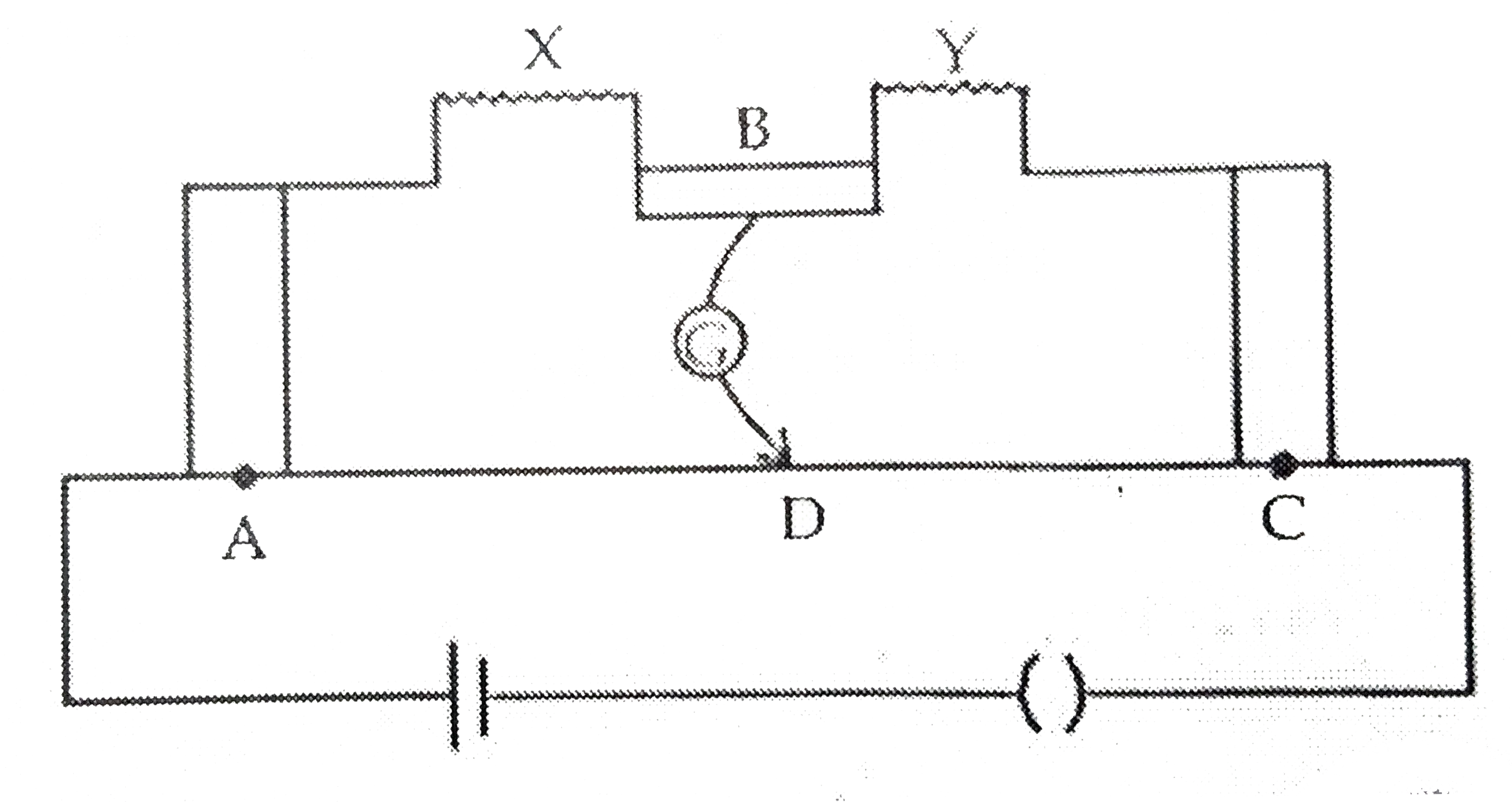
View SolutionThe Fig. shows experimental set up of a metre bridge. When the two unknown resistances X and Yare inserted, the null point Dis obtained 40 cm from the end A. When a resistance of 10Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10Ω resistance is instead | А connected in series with resistance ‘Y. Determine the values of the resistances X and Y.
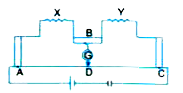
View SolutionThe figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10Ω resistance is instead connected in series with resistance 'Y'. Determine the value of the resistance X and Y
View SolutionTwo unknown resistances X and Y are placed on the left and right gaps of a meter bridge. The null point in the galvanometer is obtained at a distance of 80cm from left. A resistance of 100Ω is now connected in parallel across X. The null point is then found by shifting the sliding contact toward left by 20cm. Calculate X and Y.
View Solution(a) State Kirchhoff's rules for an electirc network. Using Kirchhoff's rules, obtain the balance condition in terms of the resistances of four arms of Wheatstone bridge.
(b) In the meter bridge experimental set up, shown in the figure, the null point 'D' is obtained at a distance of 40 cm from end A of the meter bridge wire. If a resistance of 10Ω is connected in series with R1, null point is obtained at AD=60cm. Calculate the values of R1andR2.

View Solution
