In the above problem the angular velocity of the system after the particle sticks to it will be?
0.3 rad/s
5.3 rad/s
10.3 rad/s
89.3 rad/s
To solve the problem of finding the angular velocity of the system after a particle sticks to a rotating solid cylinder, we can follow these steps:
Step 1: Understand the Initial Conditions
- We have a solid cylinder with:
- Mass (M) = 2 kg
- Radius (R) = 0.2 m
- Initial angular velocity (ω) = 3 rad/s
- A particle with:
- Mass (m) = 0.5 kg
- Velocity (v) = 5 m/s strikes the cylinder tangentially.
Step 2: Calculate the Initial Angular Momentum
The initial angular momentum (L_initial) of the system consists of two parts:
1. The angular momentum of the cylinder (L_cylinder).
2. The angular momentum of the particle (L_particle).
Angular momentum of the cylinder:
Lcylinder=Icylinder⋅ω
Where Icylinder=12MR2.
Calculating Icylinder:
Icylinder=12⋅2⋅(0.2)2=12⋅2⋅0.04=0.04kg m2
Now, calculating Lcylinder:
Lcylinder=0.04⋅3=0.12kg m2/s
Angular momentum of the particle:
The angular momentum of the particle when it strikes the cylinder is given by:
Lparticle=m⋅v⋅R
Lparticle=0.5⋅5⋅0.2=0.5kg m2/s
Total initial angular momentum:
Linitial=Lcylinder+Lparticle=0.12+0.5=0.62kg m2/s
Step 3: Calculate the Final Moment of Inertia
After the particle sticks to the cylinder, the final moment of inertia (I_final) is the sum of the moment of inertia of the cylinder and the moment of inertia of the particle.
Moment of inertia of the particle:
Iparticle=m⋅R2=0.5⋅(0.2)2=0.5⋅0.04=0.02kg m2
Total final moment of inertia:
Ifinal=Icylinder+Iparticle=0.04+0.02=0.06kg m2
Step 4: Apply Conservation of Angular Momentum
According to the conservation of angular momentum:
Linitial=Lfinal
Where:
Lfinal=Ifinal⋅ω′
Thus:
0.62=0.06⋅ω′
Step 5: Solve for Final Angular Velocity (ω')
Rearranging the equation gives:
ω′=0.620.06
Calculating:
ω′=10.33rad/s
Final Answer
The angular velocity of the system after the particle sticks to the cylinder is approximately 10.33 rad/s.
---
- We have a solid cylinder with:
- Mass (M) = 2 kg
- Radius (R) = 0.2 m
- Initial angular velocity (ω) = 3 rad/s
- A particle with:
- Mass (m) = 0.5 kg
- Velocity (v) = 5 m/s strikes the cylinder tangentially.
The initial angular momentum (L_initial) of the system consists of two parts:
1. The angular momentum of the cylinder (L_cylinder).
2. The angular momentum of the particle (L_particle).
Lcylinder=Icylinder⋅ω
Where Icylinder=12MR2.
Icylinder=12⋅2⋅(0.2)2=12⋅2⋅0.04=0.04kg m2
Lcylinder=0.04⋅3=0.12kg m2/s
The angular momentum of the particle when it strikes the cylinder is given by:
Lparticle=m⋅v⋅R
Lparticle=0.5⋅5⋅0.2=0.5kg m2/s
Linitial=Lcylinder+Lparticle=0.12+0.5=0.62kg m2/s
After the particle sticks to the cylinder, the final moment of inertia (I_final) is the sum of the moment of inertia of the cylinder and the moment of inertia of the particle.
Iparticle=m⋅R2=0.5⋅(0.2)2=0.5⋅0.04=0.02kg m2
Ifinal=Icylinder+Iparticle=0.04+0.02=0.06kg m2
According to the conservation of angular momentum:
Linitial=Lfinal
Where:
Lfinal=Ifinal⋅ω′
Thus:
0.62=0.06⋅ω′
Rearranging the equation gives:
ω′=0.620.06
ω′=10.33rad/s
The angular velocity of the system after the particle sticks to the cylinder is approximately 10.33 rad/s.
Similar Questions
Knowledge Check
In the above problem the final angular velocity of the small cylinder is
Aω04Bω0Cω02Dω08In the above problem the root mean square velocity is
A4 m/sB3.01 m/sC3 m/sD5 m/sIn the above problem the velocity of the centre of mass after 1sec will be :
A203m/s vertically downB203m/s vertically upC703m/s vertically downD703m/s vertically up.
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim.
The angular velocity of the disc after the particle sticks to it is
View SolutionIn the above question, the angular velocity will:
View Solution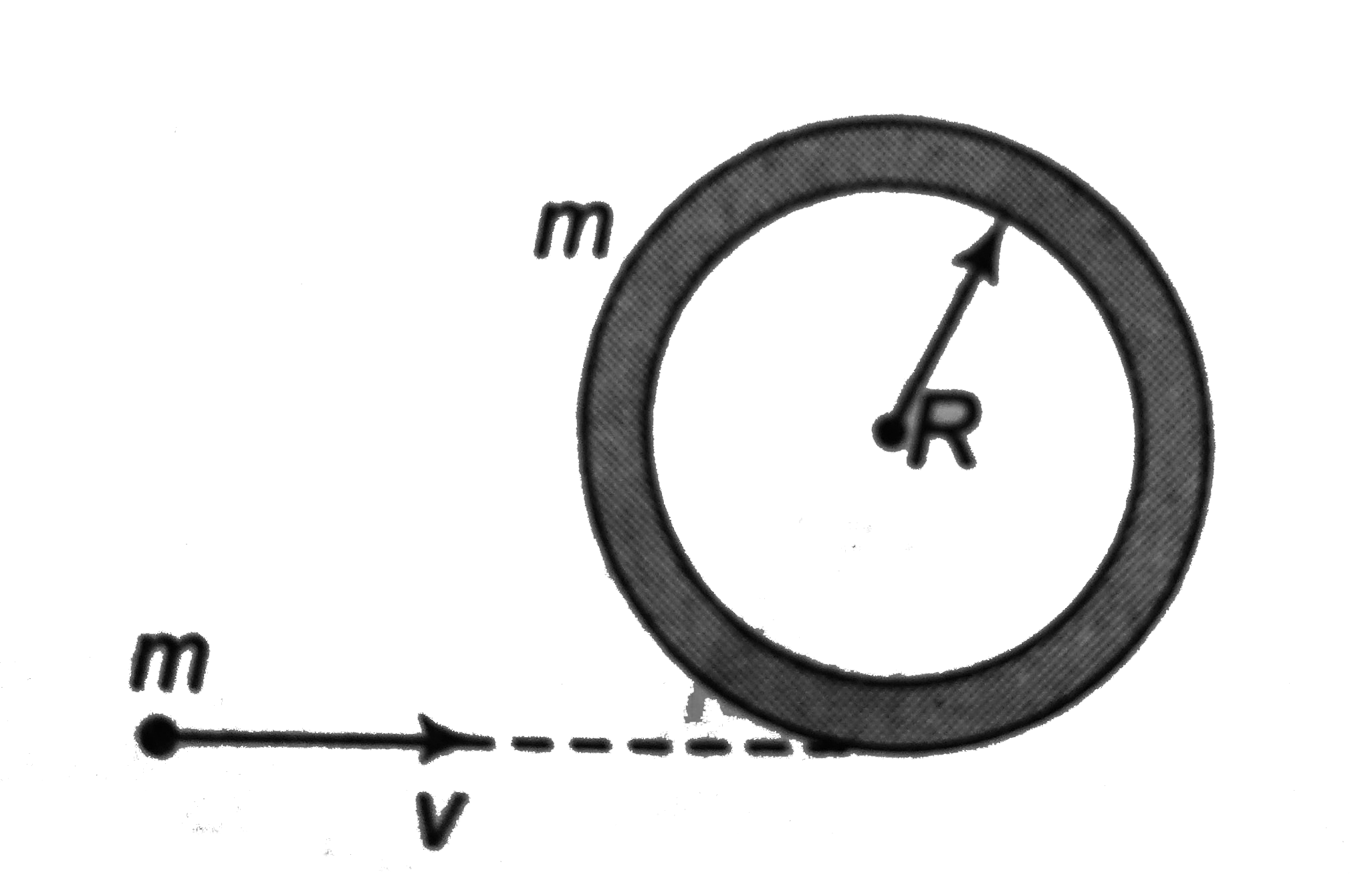
A circular ring of mass m and radius R rests flat on a horizontal smooth surface as shown in figure. A particle of mass m, and moving with a velocity v. Collides inelastically (e=0) with the ring the angular velocity with which the system rotates after the particle strikes the ring is
View SolutionA bar of mass 'm' length 'l' is in pure translatory motion with its centre velocity 'v' It collides with another identical bar which is in rest and sticks to it.
Assume that after the collision it becomes one system, then the angular velocity of the system after the collision is.
 .
.
View SolutionA bar of mass 'm' length 'l' is in pure translatory motion with its centre velocity 'v' It collides with another identical bar which is in rest and sticks to it.
Assume that after the collision it becomes one system, then the angular velocity of the system after the collision is.
 .
.
View Solution
