A wheel of mass M and radius a and M.I. IG (about centre of mass) is set rolling with angular velocity ω up a rough inclined plane of inclination theta. The distance traveled by it up the plane is
IGω22mgsinθ
ω2(Ma2+IG)2Mgsinθ
IGω22ωMgsinθ
IGω2Mgsinθ
The correct Answer is:2
To solve the problem of a wheel rolling up a rough inclined plane, we will use the principle of conservation of energy. The wheel has both translational and rotational kinetic energy initially, and as it rolls up the incline, it will convert this energy into gravitational potential energy until it comes to a stop.
1. Identify the Initial Conditions:
- Mass of the wheel: M
- Radius of the wheel: a
- Moment of inertia about the center of mass: IG
- Initial angular velocity: ω
- Inclination of the plane: θ
2. Determine the Initial Kinetic Energy:
The wheel has both translational and rotational kinetic energy.
- Translational kinetic energy (Kt):
Kt=12Mv2
- Rotational kinetic energy (Kr):
Kr=12IGω2
- The relationship between translational velocity v and angular velocity ω for pure rolling is:
v=aω
- Substituting v into the translational kinetic energy:
Kt=12M(aω)2=12Ma2ω2
- Therefore, the total initial kinetic energy Ki is:
Ki=Kt+Kr=12Ma2ω2+12IGω2
3. Determine the Final Conditions:
When the wheel comes to a stop at distance L up the incline, all kinetic energy is converted into potential energy:
- Potential energy (Uf) at height h:
Uf=Mgh=MgLsinθ
- Since the wheel comes to rest, the final kinetic energy Kf=0.
4. Apply Conservation of Energy:
The initial kinetic energy equals the potential energy at the maximum height:
Ki=Uf
12Ma2ω2+12IGω2=MgLsinθ
5. Rearranging the Equation:
Factor out 12ω2:
12ω2(Ma2+IG)=MgLsinθ
Rearranging for L:
L=12ω2(Ma2+IG)Mgsinθ
6. Final Expression for Distance L:
Thus, the distance traveled by the wheel up the inclined plane is:
L=(Ma2+IG)ω22Mgsinθ
- Mass of the wheel: M
- Radius of the wheel: a
- Moment of inertia about the center of mass: IG
- Initial angular velocity: ω
- Inclination of the plane: θ
The wheel has both translational and rotational kinetic energy.
- Translational kinetic energy (Kt):
Kt=12Mv2
- Rotational kinetic energy (Kr):
Kr=12IGω2
- The relationship between translational velocity v and angular velocity ω for pure rolling is:
v=aω
- Substituting v into the translational kinetic energy:
Kt=12M(aω)2=12Ma2ω2
- Therefore, the total initial kinetic energy Ki is:
Ki=Kt+Kr=12Ma2ω2+12IGω2
When the wheel comes to a stop at distance L up the incline, all kinetic energy is converted into potential energy:
- Potential energy (Uf) at height h:
Uf=Mgh=MgLsinθ
- Since the wheel comes to rest, the final kinetic energy Kf=0.
The initial kinetic energy equals the potential energy at the maximum height:
Ki=Uf
12Ma2ω2+12IGω2=MgLsinθ
Factor out 12ω2:
12ω2(Ma2+IG)=MgLsinθ
Rearranging for L:
L=12ω2(Ma2+IG)Mgsinθ
Thus, the distance traveled by the wheel up the inclined plane is:
L=(Ma2+IG)ω22Mgsinθ
Similar Questions
A uniform solid sphere of radius R, rolling without sliding on a horizontal surface with an angular velocity ω0, meets a rough inclined plane of inclination θ=60∘. The sphere starts pure rolling up the plane with an angular velocity ω Find the value of ω.

View SolutionA solid cylinder rolls up an inclined plane of inclination θ with an initial velocity v. How far does the cylinder go up the plane ?
View Solution
Knowledge Check
A solid cylinder is rolling down a rough inclined plane of inclination θ. Then
AThe friction force is dissipativeBThe friction force is necessarily changingCThe friction force will aid rotation but hinder translationDThe friction force is reduced if θ is reducedA solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
A75gsinθB27gsinθC37gsinθD57gsinθA hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
AFriction opposes its translationBFriction supports rotation motionCOn decreasing θ, frictional force decreasesDAll of these
A body of mass 10kg is lying on a rough inclined plane of inclination 37∘ and μ=1/2 , the minimum force required to pull the body up the plane is
View SolutionA sphere of mass m is rotated about its axis by an angular velocity ω and lowered gently on an inclined plane as shown in figure. Then initally
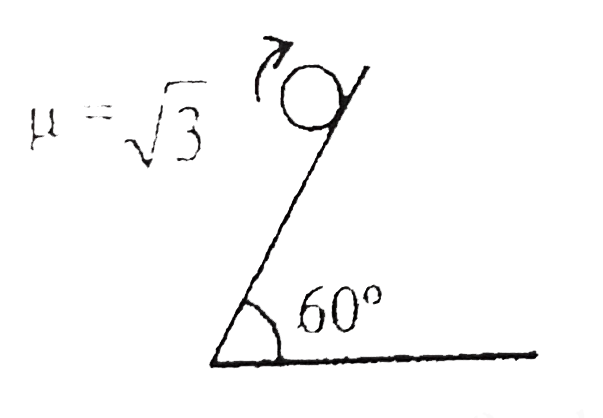
View SolutionA solid cylinder of mass m and radius r is rolling on a rough inclined plane of inclination θ. The coefficient of friction between the cylinder and incline is μ. Then.
View SolutionA solid cylinder roll up without slipping an inclined plane of inclination θ with an initial velocity v. How for does the cylinder go up the plane :-
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View Solution