Calculate the moment of inertia of
a. a ring of mass M and radius R about an axis coinciding with the diameter of the ring.
b. a thin disc about an axis coinciding with the diameter.
Video Solution
Text Solution
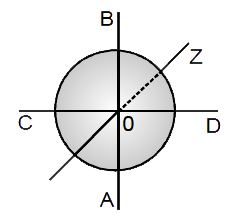
Let X and Y axes be along two perpendicular diameters of the ring. By symmetry, Ix=IyandIx+Iy But we know that Iz=MR2 MR2=Ix+Iy ,MR2=2Ix Ix=Iy=MR22Similarly for a thin disc (i.e., a circular plate) Moment of inertia about a diameter is =I=12(12MR2)=14MR2.

|
Similar Questions
Knowledge Check
Moment of inertia of a disc of mass 'M' and radius 'R' about the diameter is
AMR22BMR24CMR23DMR212Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
A52MR2B32MR2C12MR2DMR2Moment of inertia of a ring of mass M and radius R about a tangent to the circle of the ring is
AMR2B12MR2C32MR2D72MR2
The moment of inertia of a ring of mass M and radius R about PQ axis will be :-

View SolutionFind the moment of inertia of uniform ring of mass M and radius R about a diameter.
View SolutionThe moment of inertia of a thin circular disc of mass M and radius R about any diameter is
View SolutionThe moment of inertia of a thin circular disc of mass M and radius R about any diameter is
View SolutionThe M.I. of a thin ring of mass M and radius R about an axis through the diameter in its plane will be:
View Solution

