A stationary object is released from a point P a distance 3R from the centre of the moon which has radius R and mass M. which one of the following expressions gives the speed of the object on hitting the moon?

${(\frac{2 G M}{3 R})}^{1 / 2}$

${(\frac{4 G M}{3 R})}^{1 / 2}$

${(\frac{G M}{3 R})}^{1 / 2}$

${(\frac{G M}{R})}^{1 / 2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Answer

Step by step video, text & image solution for A stationary object is released from a point P a distance 3R from the centre of the moon which has radius R and mass M. which one of the following expressions gives the speed of the object on hitting the moon? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS GRAVITATION

Topper's Solved these Questions

Knowledge Check

A point mass $m$ is released from rest at a distance of $3 R$ from the centre of a thin-walled hollow sphere of radius $R$ and mass $M$ as shown. The hollow sphere is fixed in position and the only force on the point mass is the gravitational attraction of the hollow sphere. There is a very small hole in the hollow sphere through which the point mass falls as shown. The velocity of a point mass when it passes through point $P$ at a distance $R / 2$ from the centre of the sphere is

A $\sqrt{\frac{2 G M}{3 R}}$
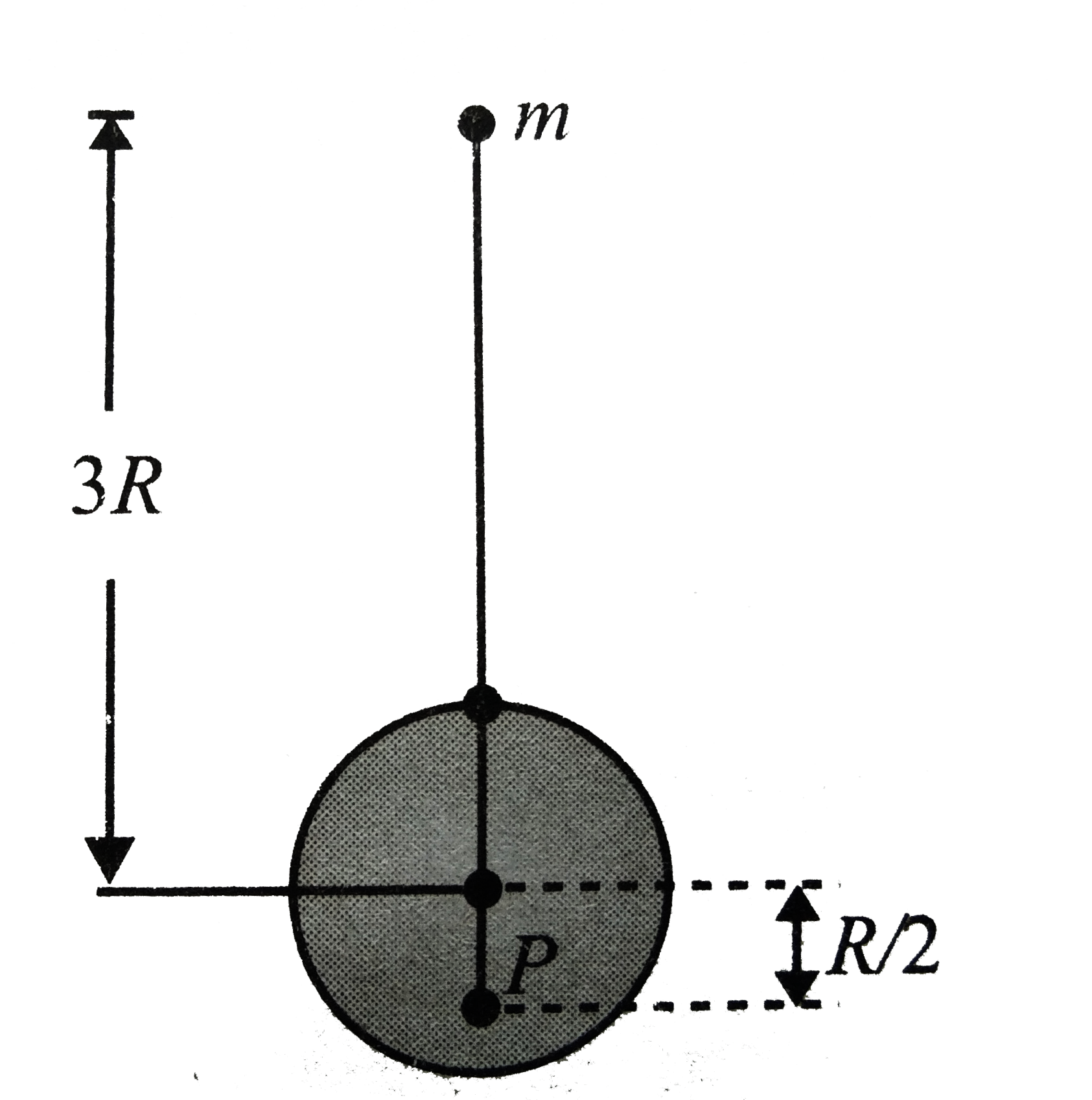B $\sqrt{\frac{5 G M}{3 R}}$
C $\sqrt{\frac{25 G M}{24 R}}$
Dnone of these
A block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R.
Which one of the following expressions gives the speed of the mass at the bottom of the hoop ?
Azero $m / s^{2}$
B $v = \frac{m g}{2 R}$
C $v^{2} = 2 g R$
D $v = m g R$
An object is propelled vertically to a maximum height of 4R from the surface of a planet of radius R and mass M. The speed of object when it returns to the surface of the planet is -
A $2 \sqrt{\frac{2 G M}{5 R}}$
B $\sqrt{\frac{G M}{2 R}}$
C $\sqrt{\frac{3 G M}{2 R}}$
D $\sqrt{\frac{G M}{5 R}}$

AAKASH INSTITUTE-GRAVITATION -ASSIGNMENT SECTION - A (OBJECTIVE TYPE QUESTIONS)

Home
Ask Doubt
Profile

A stationary object is released from a point P a distance 3R from the centre of the moon which has radius R and mass M. which one of the following expressions gives the speed of the object on hitting the moon?

The correct Answer is:B

Topper's Solved these Questions

Similar Questions

Knowledge Check

A block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R. Which one of the following expressions gives the speed of the mass at the bottom of the hoop ?

An object is propelled vertically to a maximum height of 4R from the surface of a planet of radius R and mass M. The speed of object when it returns to the surface of the planet is -

AAKASH INSTITUTE-GRAVITATION -ASSIGNMENT SECTION - A (OBJECTIVE TYPE QUESTIONS)

A block of mass m is released from rest at a height R above a horizontal surface. The acceleration due to gravity is g. The block slides along the inside of a frictionless circular hoop of radius R.
Which one of the following expressions gives the speed of the mass at the bottom of the hoop ?