Compare the power used in the 2Ω resistor in each of the following circuits :
(i) a 6V battery in series with 1Ωand2Ω resistors, and
(ii) a 4V battery in parallel with 12Ωand2Ω resistors.
(i) In the First Case:
Potential difference, V=6V
Current, I=? (To be calculated)
And, Resistance, R=1Ω+2Ω (Resistors in series)
R=3Ω
Now, by Ohm's law (for whole circuit) : VI=R
So, 6I=3
And, Current, I=63
I=2A
Thus, the current flowing in the circuit containing 1Ω and 2Ω resistors in series is 2 A. In series circuit, the same current flows throughout the circuit. So, the current flowing through the 2Ω resistor is also 2A [Figure (i)].Now, we know that the current (in 2Ω resistor) is 2A and its resistance is 2Ω.

So, Power used in 2Ω resistor, P1=I2×R
(In first case) P1=(2)2×2
P1=4×2
P1=8W ...(1)
Thus, the power P1 used in 2Ω resistor in the first case is 8 watts.
(ii) In the Second Case:
Here 4 V battery is attached across the parallel combination of 12Ω and 2Ω resistors, so the potential difference across the 2Ω resistor will also be 4V [see Figure (ii)].
Now, Potentil difference, V=4V (Across the 2Ω resistor)
And, Resistance, R=2Ω
So, Power used in 2Ω resistor, P2=V2R
P2=(4)22
P2=162
P2=8W ...(2)
Thus, the power P2 used in the 2Ω resistor in the second case is also 8 watts.
In order to compare the power used in 2Ω resistor in the two circuits, let us divide P1 by P2.
So, P1P2=8W8W
or P1P2=1
or P1=P2
The 2Ω resistor uses equal power in both the circuits.

Topper's Solved these Questions
- ELECTRICITY BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - ELECTRICITY EXERCISE - Very Short Answer Type Questions
1 Videos
- ELECTRICITY BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - ELECTRICITY EXERCISE - Short Answer Type Questions
2 Videos
- ELECTRICITY BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - ELECTRICITY EXERCISE - Sample Problem
1 Videos
- MAGNETIC EFFECT OF ELECTRIC CURRENT BOOK - LAKHMIR SINGH & MANJIT KAURCHAPTER - MAGNETIC EFFECT OF ELECTRIC CURRENT EXERCISE - NCERT BOOK
2 Videos
Similar Questions
Compare the power used in the 2Ω resistor in each of the following circuits: (i) a 6V battery in series with 1Ωand2Ω resistors, and (ii) a 4V battery in parallel with 12Ωand2Ω resistors.
View SolutionCompare the power used in the 2Ω resistor in each of the following circuits:
(i) a 6 V battery in series with 1Ω and 2Ω resistors, and (ii) a 4 V battery in parallel with 12Ω and 2Ω resistors.
View Solution
Knowledge Check
If power dissipated in the 9Ω resistor in the resistor shown is 36W, the potential difference across the 2Ω resistor is
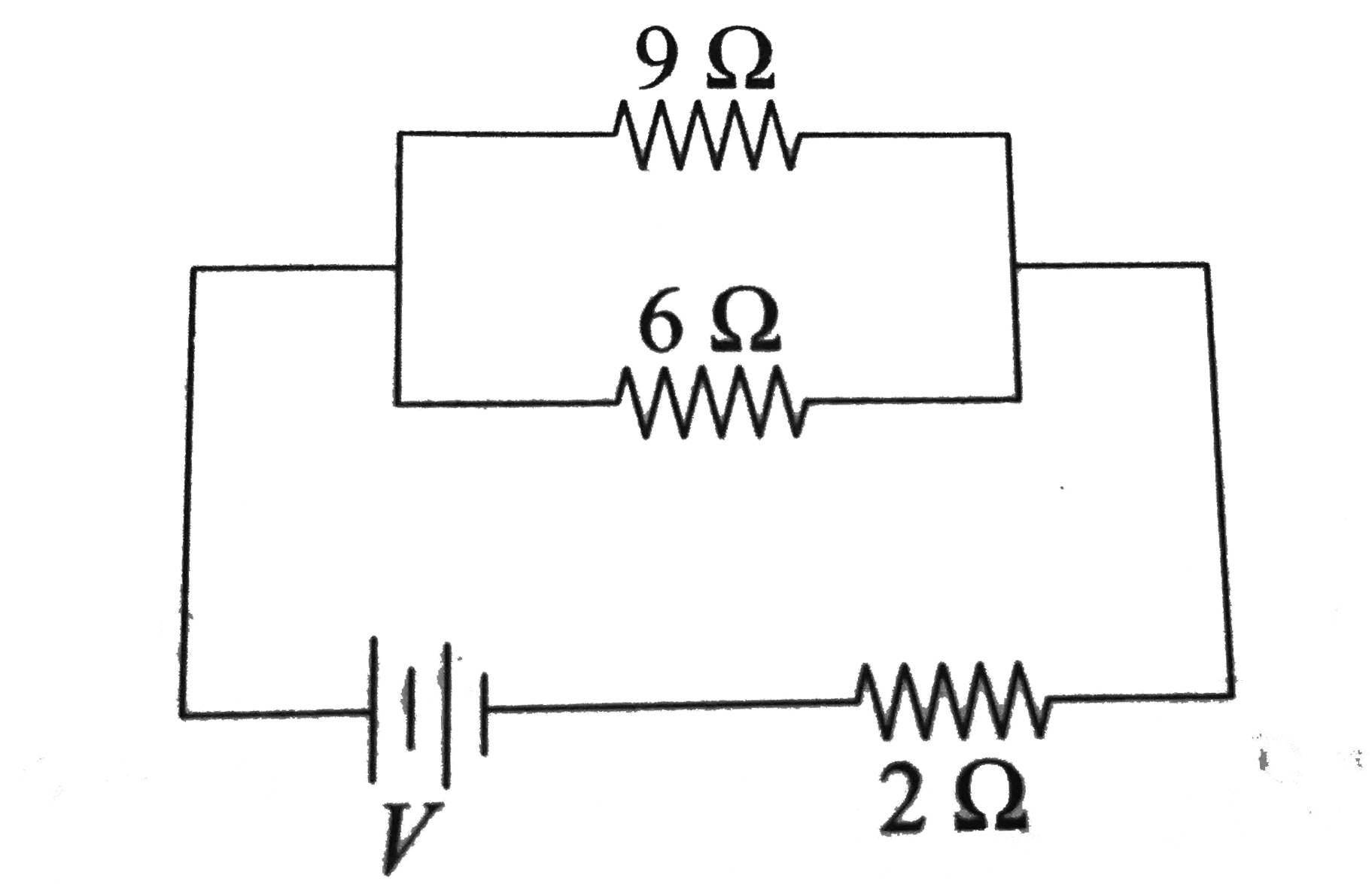 A8VB10VC2VD4V
A8VB10VC2VD4VThe power dissipated in 3Ω resistor in the circuits as shown in the figure is 2W. The power dissipated in 7Ω resistor will be
 A14WB143WC73WD7W
A14WB143WC73WD7WTwo resistors of resistances 2Ωand4Ω when connected to a battery will have :
Asame current flowing through them when connected in parallelBsame current flowing through them when connected in seriesCsame potential difference across them when connected in seriesDdifferent potential differences across them when connected in parallel.
Compare the power used in the 2 ω resistor in each of the following circuits :
a 6 V battery in series with 1 ω and 2 ω resistors, and
View SolutionCompare the power used in the 2 ω resistor in each of the following circuits :
a 4 V battery in parallel with 12 ft and 2 ft resistors.
View SolutionIn the following circuit, the current drawn from the battery is 2A. If the 5Ω resistance is replaced by a 20Ω resistor, then the current drawn from the battery will be
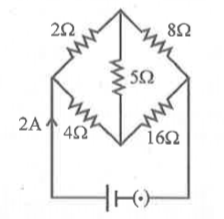
View Solution6Ω and 12Ω resistors are connected in parallel. This combination is connected in series with 10 V battery and 6Ω resistor. What is the potential differnce between the terminals of the 12Ω resistor ?
View SolutionA current of 3A flows through the 2Ω resistor shown in the circuit the power dissipated in the 5Ω resistor is
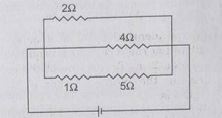
View Solution
