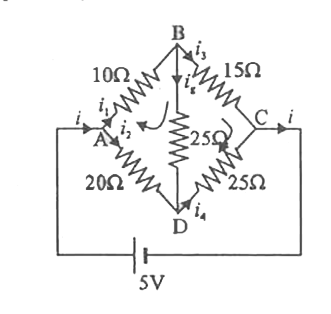
ABCD forms the four arms of a Wheatstone's network. The arms AB, BC, CD, DA are of 10Ω,15Ω,25Ω and 20Ω respectively. The junctions B and D are connected to the ends of galvanometer of resistance 25Ω. If the source voltage is 5V, r = 0, then calculate the current in the galvanometer. Assume the branch currents across AB, BC, CD, DA and BD as i1,i3,−i4,−i2, and ig respectively.Solution in Kannada
Applying KCL to the nodes A, B, C and D
we get i2=i−i1,i3=i1−ig,
i3+i4=i,∴i4=i−i1+ig
Applying KVL to the mesh ABDA we get,
10i1+25ig−20i2=0
or 2i1+5ig−4i2=0
Applying KVL to the mesh BCDB we get,
15(i1−ig)−25(i−i1+ig)−25ig=0
15i1−15ig−25i+25i1−25ig−25ig=0
40i1−65ig−25(i1+i2)=0
15i1−65ig−25i2=0
or 3i1−13ig−5i2=0
Applying KVL to the mesh ADCA we get,
20i2+25(i2+ig)=5
45i2+25ig=5
or 9i2+5ig=1 .....(3)
Using determinant method, Δ=∣∣
∣∣25−43−13−5059∣∣
∣∣=2(−117+25)−3(45+20)+0
i.e., Δ=−184−195=−379, Δig=∣∣
∣∣20−430−5019∣∣
∣∣=0+0+1(−10+12) , Δig=2
ig=ΔigΔ=2−379=−5.28 mA , Current in the galvanometer= 5.28 mA
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - SUBHASH PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - FIVE MARK QUESTIONS AND ANSWERS
6 Videos
- COMMUNICATION SYSTEMS BOOK - SUBHASH PUBLICATIONCHAPTER - COMMUNICATION SYSTEMS EXERCISE - THREE MARKS QUESTIONS WITH ANSWERS
4 Videos
- DUAL NATURE OF RADIATION AND MATTERBOOK - SUBHASH PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTEREXERCISE - NUMERICALS WITH SOLUTIONS
21 Videos
Similar Questions
Derive an expression for electrical conductivity.
View SolutionOutline the production of an Amplitude Modulated Wave.
View SolutionA photo has a wavelength of 5000 Å. Calculate its momentum.
View SolutionA galvaometer of coil resistance 100Ω is connected to a shunt of resistance 10Ω. The current throught the galvanometer is i10 , the current through the shunt is i2 and the total current into the combination is i3, then the ratio i1:i2:i3 is
View SolutionThe four arms of a Wheatstone bridge (Fig. 3.26) have the following resistances:
AB=100Ω,BC=10Ω,CD=5Ω,andDA=60Ω.

A galvanometer of 15W resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
View Solutionएक वृत्त, एक चतुर्भुज ABCD की चारों भुजाओं को अन्तः स्पर्श करता है। सिद्ध कीजिए कि-
AB + CD = AD + BC.
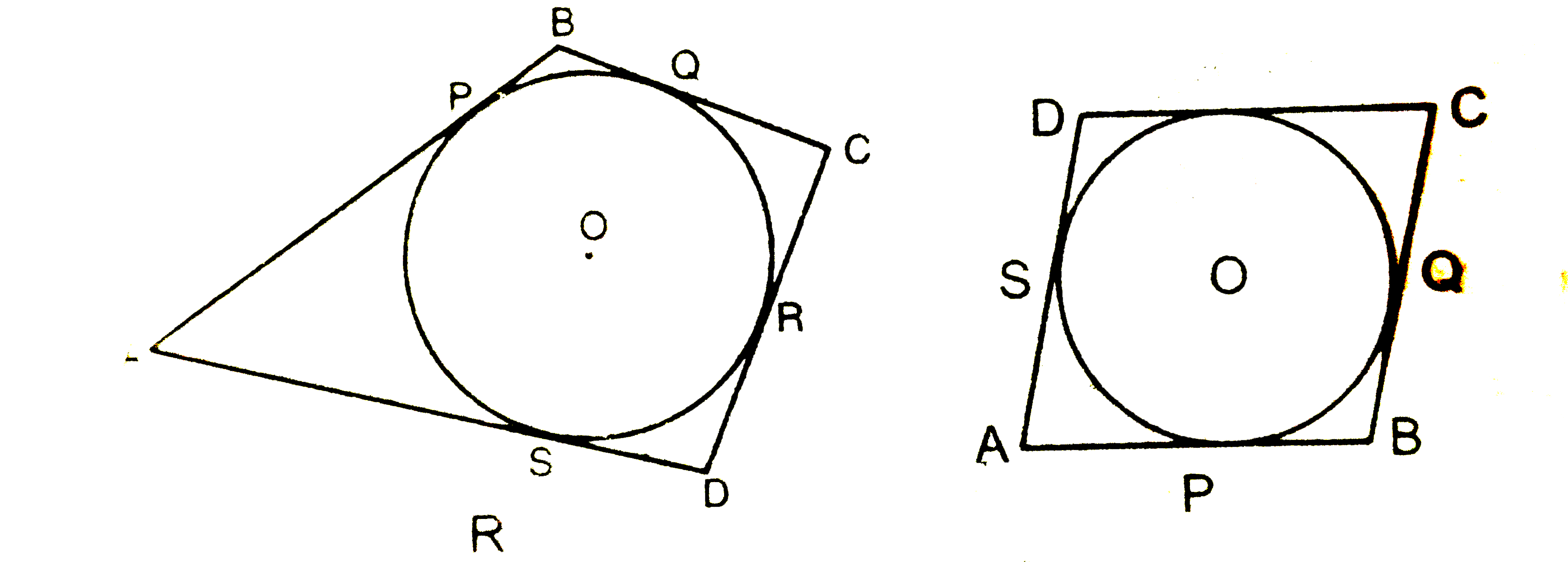
(अथवा) आकृति, में एक चतुर्भुज ABCD, O केन्द्र वाले वृत्त के परिगत इस प्रकार बनाई गई है कि भुजाएँ AB, BC, CD, तथा DA वृत्त को क्रमशः बिन्दुओं P, Q, R तथा S पर स्पर्श करती हैं। सिद्ध कीजिए कि
AB + CD = BC + DA
View SolutionThe four arms of a Wheatstone bridge have the following resistance :
AB=100Ω,BC=10Ω,CD=5Ω, and DA=60Ω
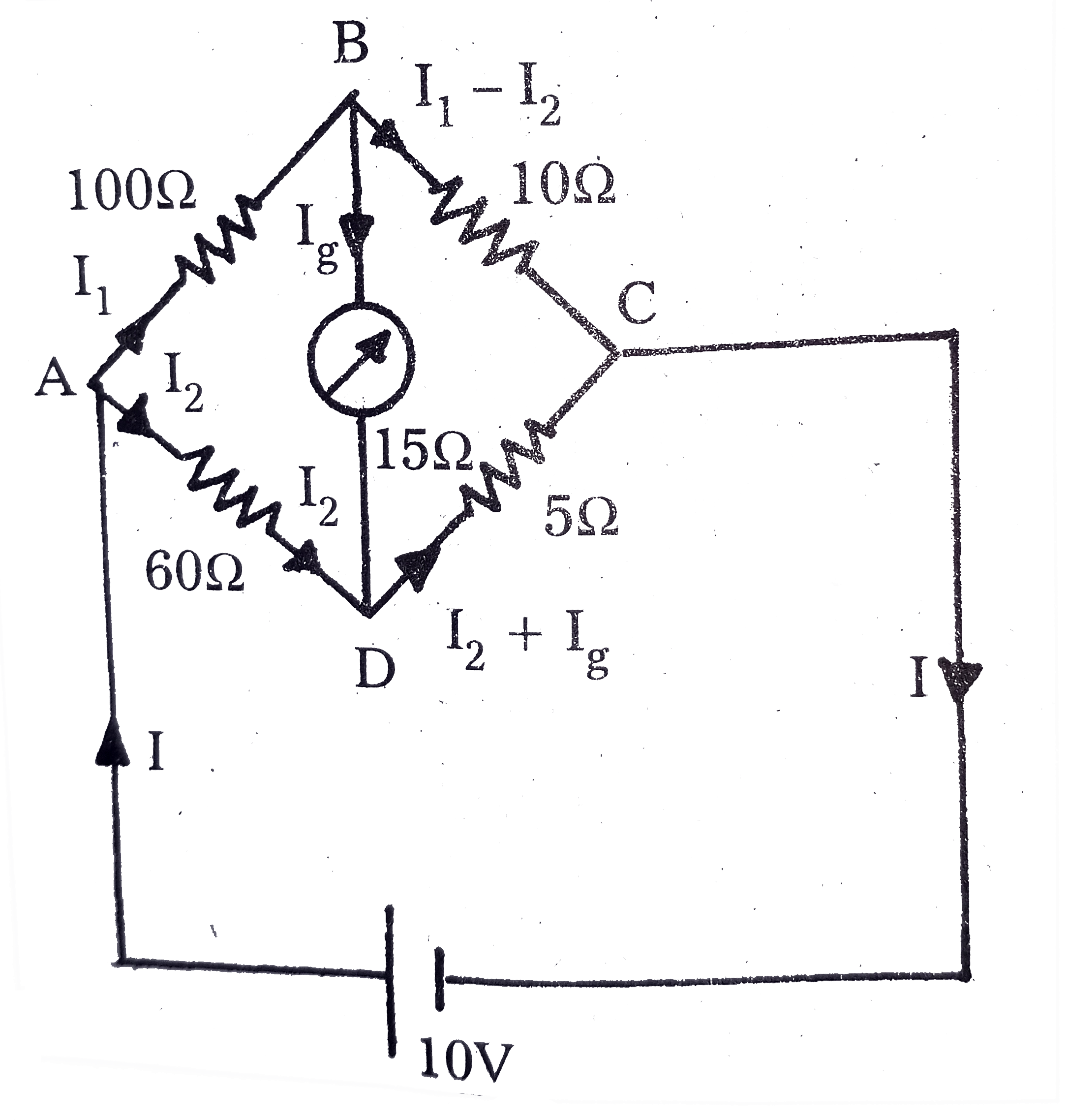
A galvanometer of 15Ω resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
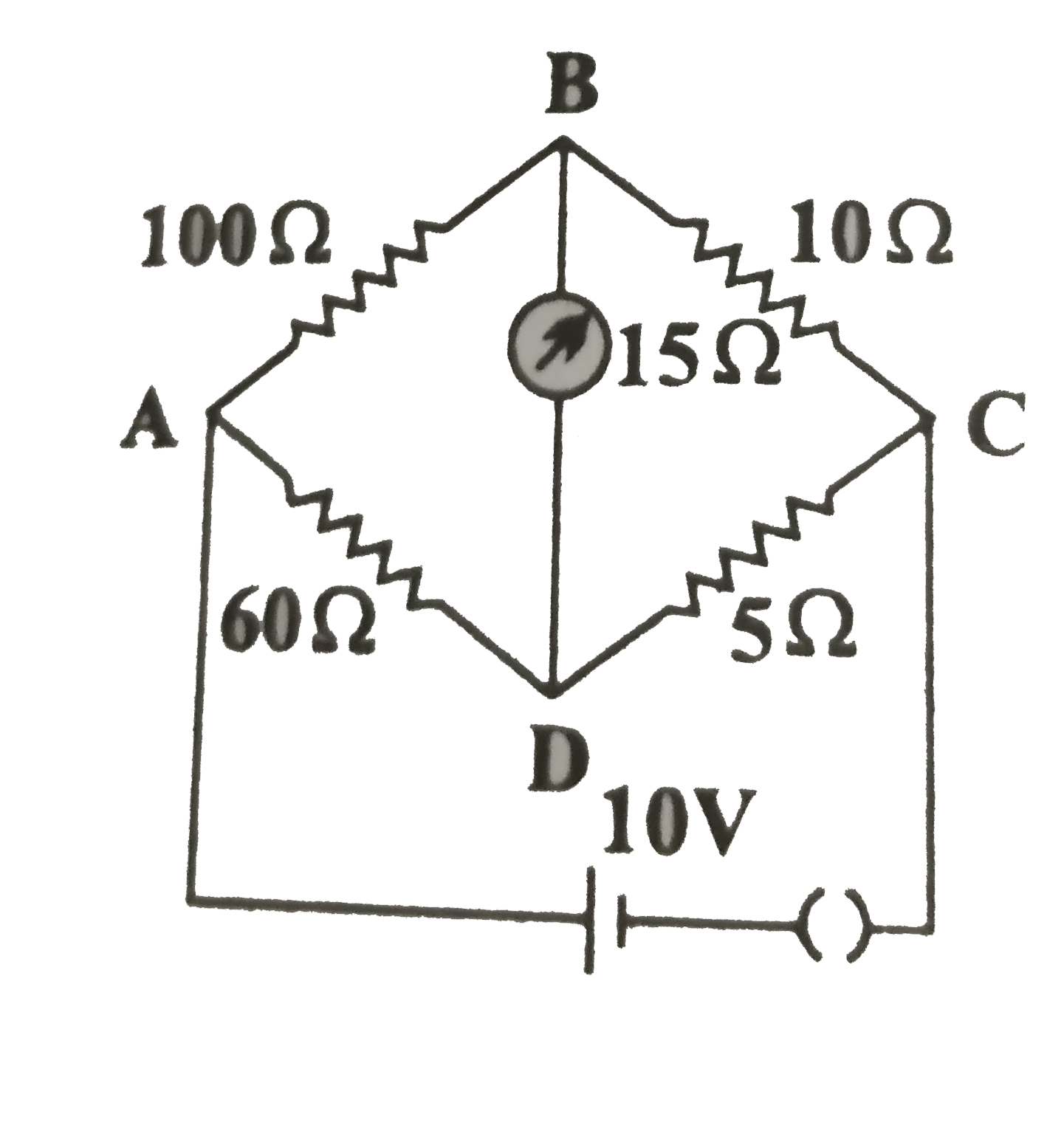
View Solutionव्हीटस्टोन सेतु के चार भुजाओं के प्रतिरोध निम्नवत है- AB=100Ω,BC=10Ω,CD=5Ω तथा DA=60Ω,15Ω प्रतिरोध के एक धारामापी को BD के बीच जोड़ा गया है। धारामापी में प्रवाहित होने वाली धारा को परिकलित कीजिए। AC के मध्य 10V विभवांतर है।
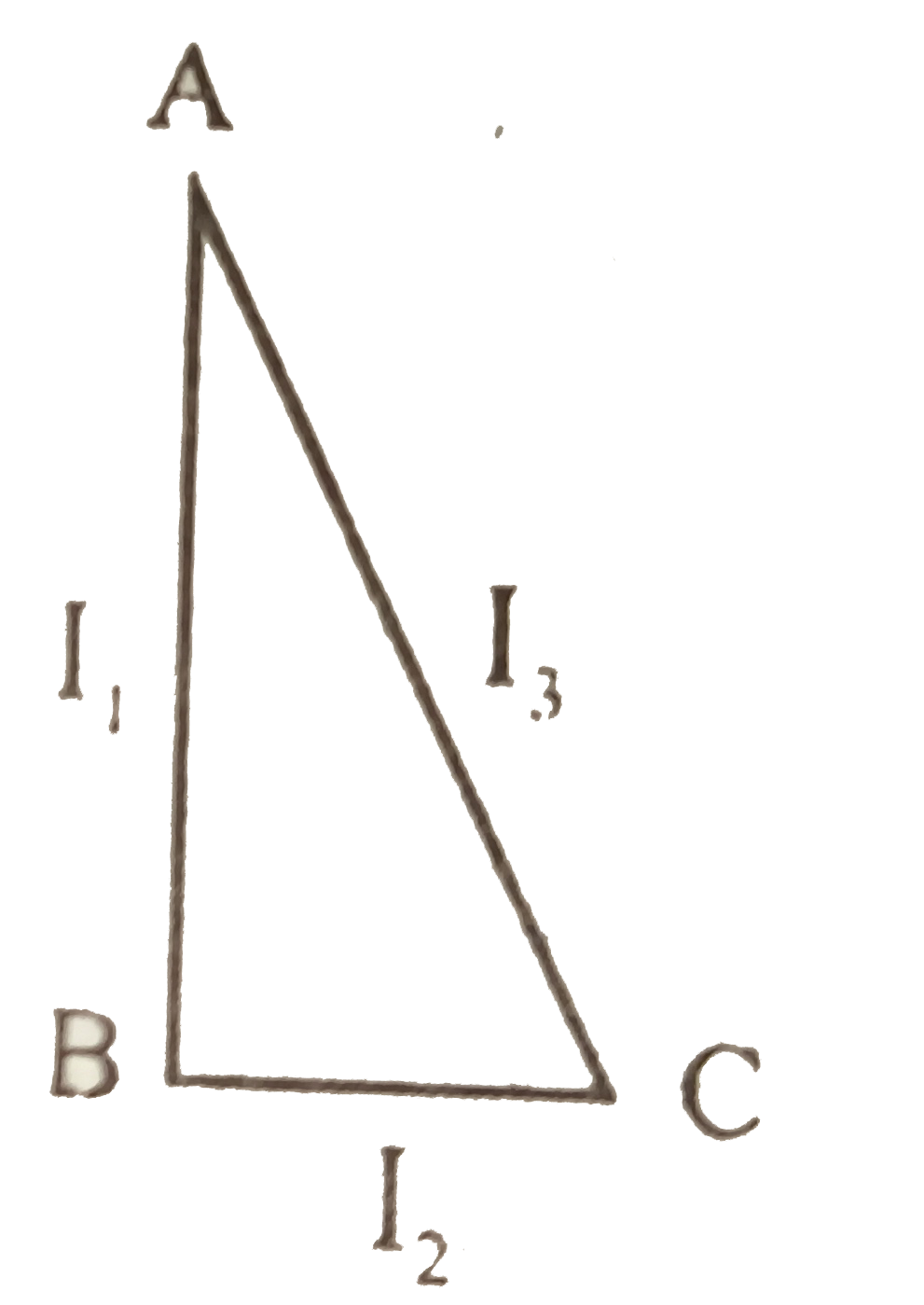
View SolutionABC एकसमान मोटाई की समकोणिक त्रिभुजाकार प्लेट है । इसकी भुजाएँ इस प्रकार हैं की AB>BC. । यदि I1,I2 तथा I3 भुजाओं AB, BC तथा AC के परितः जड़त्व - आघूर्ण हों तो निम्न में से कौन - सा संबंध सही है
View SolutionThe four arms of a Wheatstone bridge (Fig. 3.26) have the following resistances:
AB=100Ω,BC=10Ω,CD=5Ω,andDA=60Ω.

A galvanometer of 15W resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
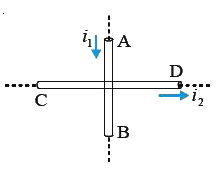
View SolutionTwo long wires AB and CD carrly currents i1 and i2 in the directions shown
View SolutionCalculate the values of currents · I_(1)I_(2)I_(3) and I_(4) Is and loin the section of networks shown in the figure
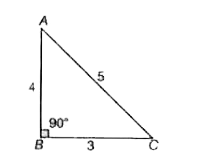
View SolutionABC एक त्रिकोणीय प्लेट है | भुजाएँ चित्र में दी गई है | IAB,IBC तथा ICA क्रमश : AB,BC तथा CA अक्ष के परितः जड़त्व आघूर्ण है | निम्न में से कौन- सा सम्बन्ध सही है ?
View SolutionThe four arms as a Wheatstone bridge have the following resistances:
AB=100Ω,BC=10Ω,CD=5ΩandDA=60Ω
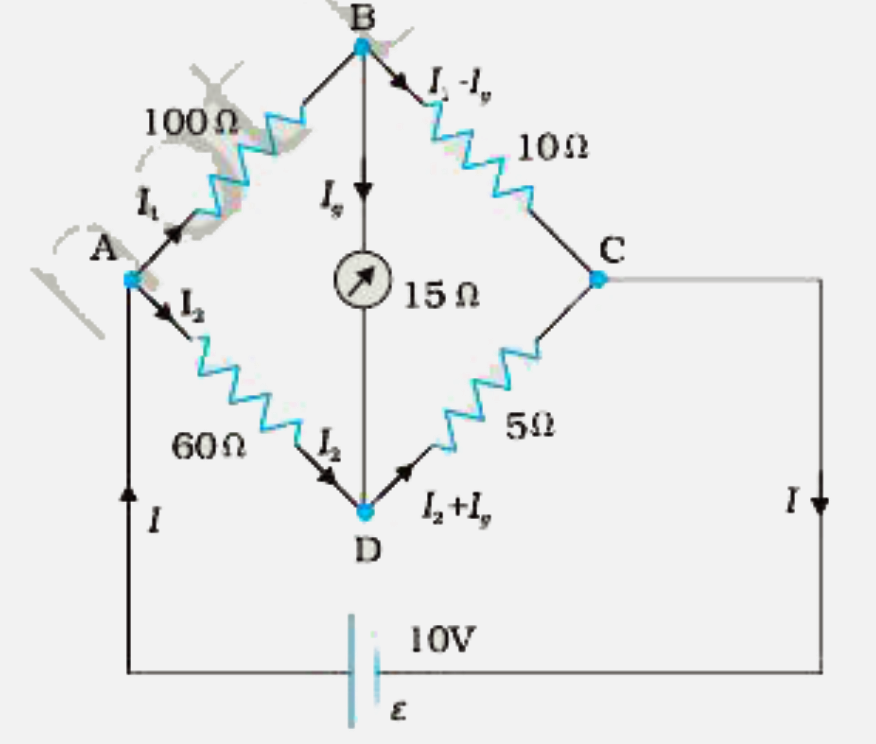
A galvanometer of 15Ω resistacne is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
View Solution(a) Define current sensitivity of a galvanometer. Write its expression. (b) A galvanometer has resistance and shows full scale deflection for currently I_(g) . (i) How can it be converted into an ammeter to measure current up to I_(0) (I_(0) gt I_(g)) (ii) What is the effective resistance of this ammeter ?
View Solution
