The four arms of a Wheatstone bridge (Fig. 3.26) have the following resistances:
AB=100Ω,BC=10Ω,CD=5Ω,andDA=60Ω.

A galvanometer of 15W resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
Considering the mesh BADB, we have
100I1+15Ig−60I2=0
or 20I1+3Ig−12I2=0
Considering the mesh BCDB, we have
10(I1−Ig)−15Ig−5(I2+Ig)=0
10I1−30Ig−5I2=0
2I1−6Ig−I2=0
Consideringn the mesh ADCEA,
60I2+5(I2+Ig)=10
64I2+5Ig=10
13I2+Ig=2
Multiplying Eq, (2.84b) by 10
20I1−60Ig−10I2=0
From Eqs. (2.84d) we have
63Ig−2I2=0
I2=31.5Ig
Substituting the value of I2 into Eq. [3.84 (c)], we get
13(31.5Ig)+Ig=2
410.5Ig=2
Ig=4.87mA.
Topper's Solved these Questions
Similar Questions
The four arms of a Wheatstone bridge (Fig. 3.26) have the following resistances:
AB=100Ω,BC=10Ω,CD=5Ω,andDA=60Ω.

A galvanometer of 15W resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.
View SolutionThe four arms of a Wheatstone bridge have resistances as shown in the figure. A galvanometer of 15Ω resistance is connected across BD. Calculate the current through the galvanometer when a potential difference of 10 V is maintained across AC.

View Solution
Knowledge Check
In a typical Wheatstone network, the resistances in cyclic order are A=10Ω,B=5Ω,C=4Ω D=4Ω for the bridge to be balanced
 A10Ω should be connected in parallel with AB10Ω should be connected in series with AC5Ω should be connected in series with BD5Ω should be connected in parallel with B
A10Ω should be connected in parallel with AB10Ω should be connected in series with AC5Ω should be connected in series with BD5Ω should be connected in parallel with BThree resistances 2Ω,3Ω and 4Ω are connected in parallel. The ratio of currents passing through them when a potential difference is applied across its ends will be
A5:4:3B6:3:2C4:3:2D6:4:3
If the resistance of the galvanometer G is 15Ω, then current through the galvanometer will be
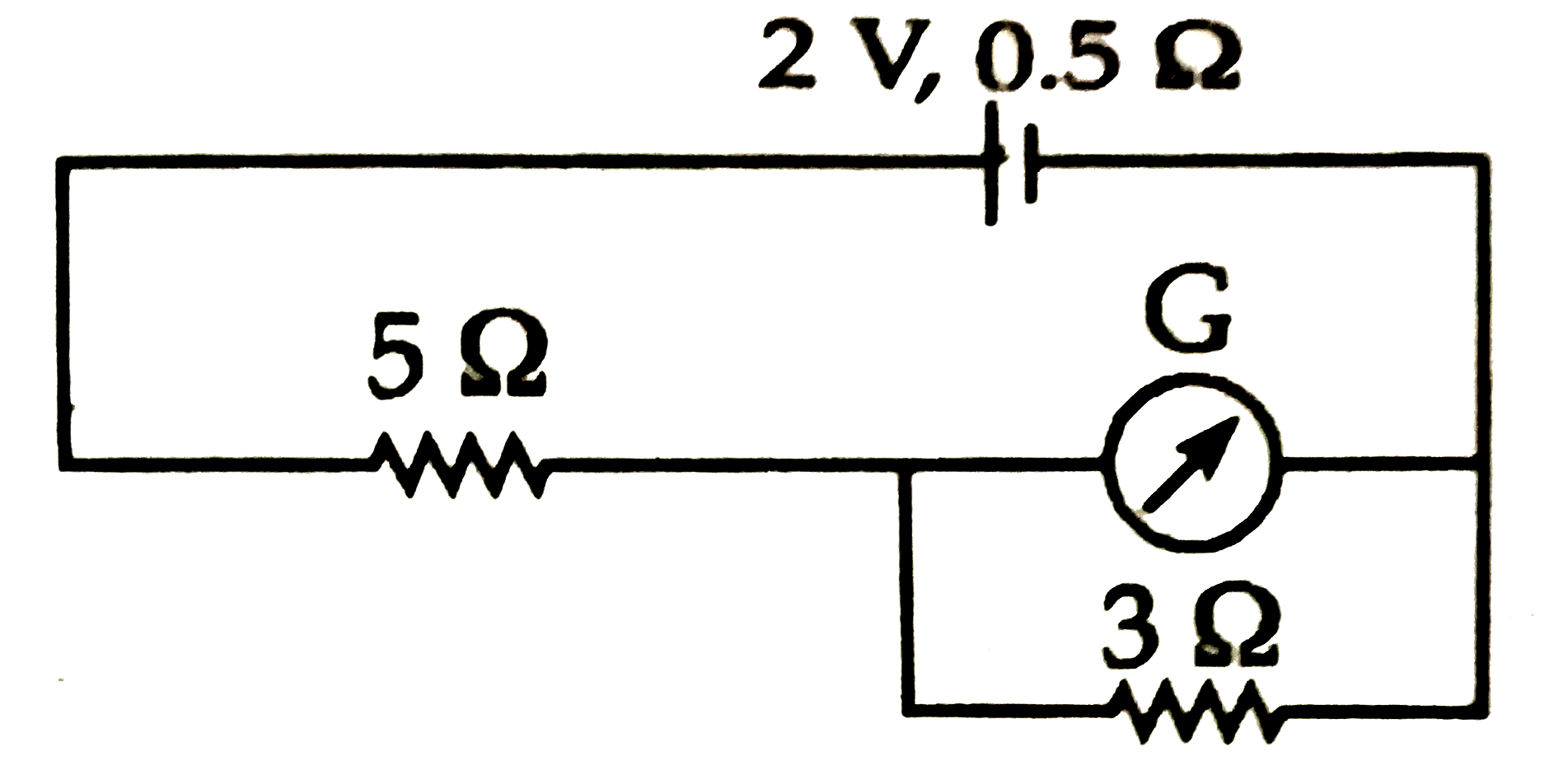
View SolutionIn Wheatstone bridge, the resistances in four arms are 10Ω,10Ω,10Ω and 20Ω. To make the bridge balance, resistance connected across 20Ω is
View SolutionA shunt of 6Ω is connected across a galvanometer of resistance 294Ω. Find the fraction of the total current passing through the galvanometer.
View SolutionIn a wheatstone bridge, the resistance of the arms of the bridge are AB = 2Ω, BC = 4Ω ,AD = 1Ω and DC = 3Ω. The terminals of negligible resistance to A and C. If a galvanometer of resistance 100Ω is connected between B and D, find the current in the galvanometer.
View SolutionFour resistances 5Ω,5Ω,8Ω and 10Ω form a Wheatstone network. Find the resistance whch connected across the 10Ω resistance will balance the network.
View SolutionA galvanometer has a resistance of 50Ω. A resistance of 5Ω is connected across its terminals. What part of the total current will flow through the galvanometer?
View Solution
