(a) Given $n$ resistors each of resistance $R$ . How will you combine them to get the (i) maximum (ii) minimum effective resistance ? What is the ratio of the maximum to minimum resistance ?
(b) Given the resistances of $1 Ω, 2 Ω, 3 Ω$ , how will you combine them to get an equivalent resistance of (i) $(11 / 3) Ω$ (ii) $(11 / 5) Ω$ (iii) $6 Ω$ (iv) $(6 / 11) Ω$ ?
(c) Determine the equivalent resistance of networks shown in Figure.

Video Solution

Text Solution

Verified by Experts

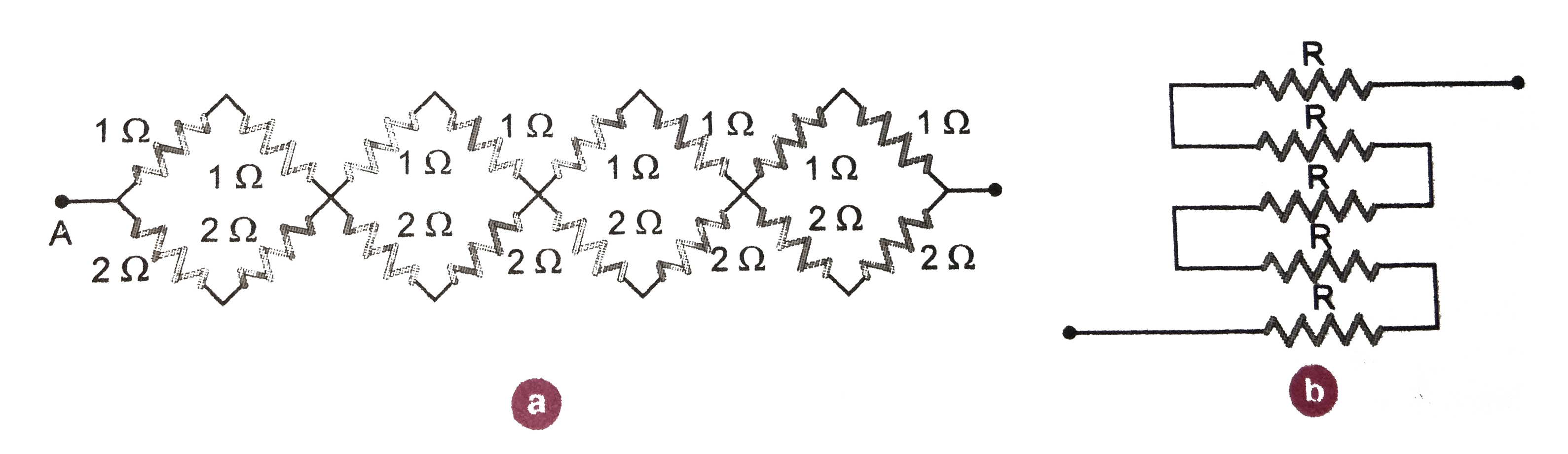
(a) Total number of resistors = n
Resistance of each resistor = R
(i) When n resistors are connected in series, effective resistances $R_{1}$ is the maximum given by the product nR
Hence, maximum resistance of the combination, $R_{1} = n R$
(ii) When n resistors are connected in parallel, the effective resistance $(R_{2})$ is the minimum, given by ratio $\frac{R}{n}$
Hence, minium resistance of the combination, $R_{2} = \frac{R}{n}$
(iii) The ratio of the maximum to the minimum resistance is,
$\frac{R_{1}}{R_{2}} = \frac{n R}{\frac{R}{n}} = n^{2}$
(b) The resistance of the given resistors is,
$R_{1} = 1 Ω, R_{2} = 2 Ω, R_{3} = 3 Ω 2$
(i) Equilivalent resistance, $R = \frac{11}{3} Ω$
Consider the following combination of the resistors

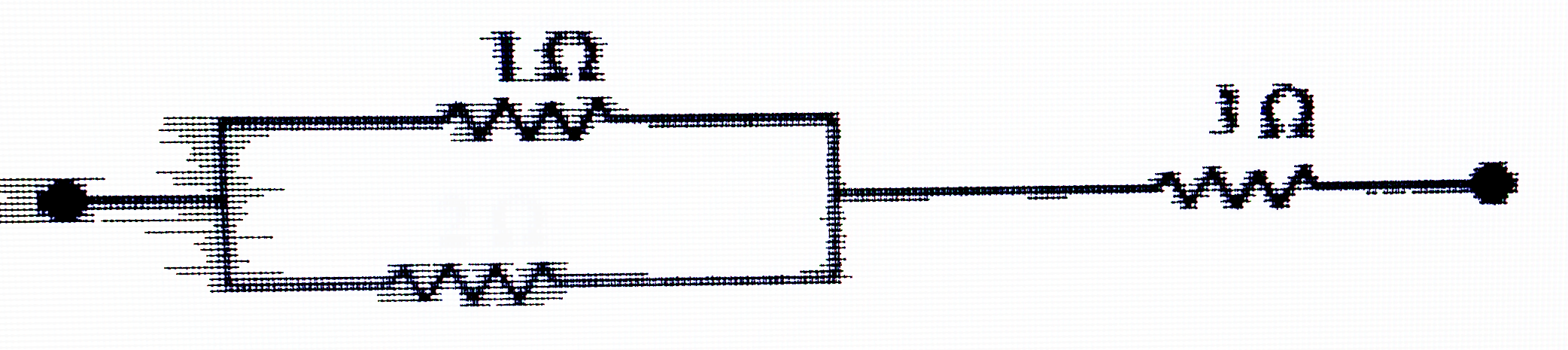
Equilivalent resistance of the circuit is given by,
$R = \frac{2 \times 1}{2 + 1} + 3 = \frac{2}{3} + 3 = \frac{11}{3} Ω$
Equilivalent resistance of the circuit is given by,
$R = \frac{2 \times 1}{2 + 1} + 3 = \frac{2}{3} + 3 = \frac{11}{3} Ω$
(ii) Equilivalent resistance, $R = \frac{11}{5} Ω$
Consider the following combination of the resistors

Equilvalent resistance of the circuit is given by,
$R' = \frac{2 \times 3}{2 + 3} + 1 = \frac{6}{5} + 1 = \frac{11}{5} Ω$
(iii) Equivalent resistance. $R = 6 Ω$
Consider the series combination of the resistor, as shown in the given circuit

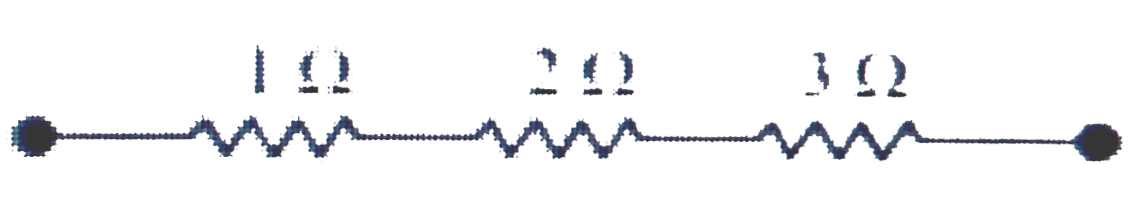
Equivalent resistane of the circuit is given by the sum,
$R = 1 + 2 + 3 = 6 Ω$
(iv) Equivalent resistance, $R = \frac{6}{11} Ω$
Consider the series combination of the resistors, as shown in the given circuit

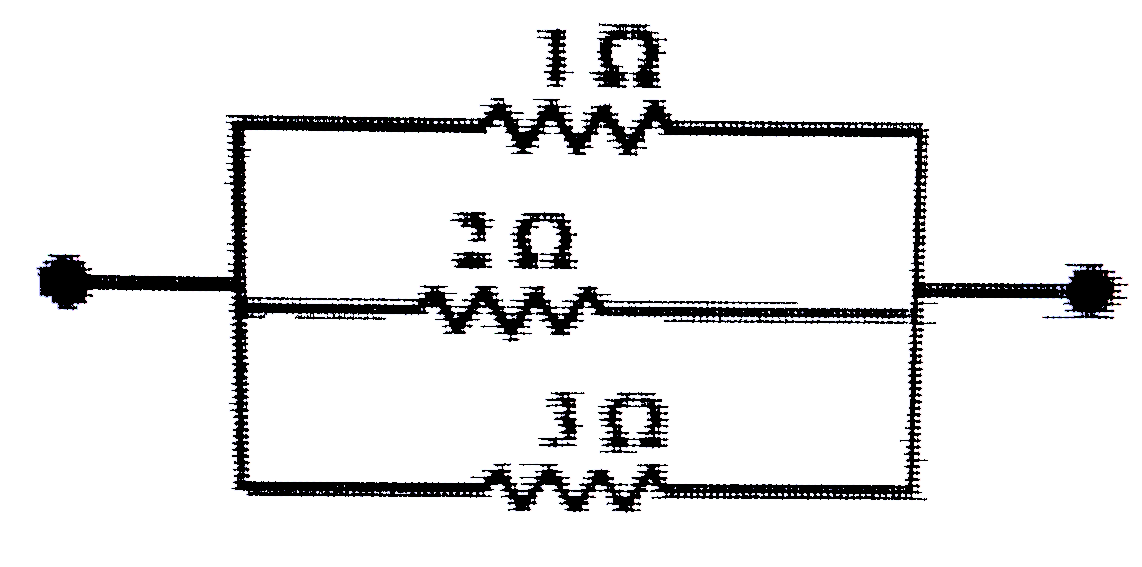
Equivalent resistance of the circuit is given by
$R = \frac{1 \times 2 \times 3}{1 \times + 2 \times 3 + 3 \times 1} = \frac{6}{11} Ω$
(c) (a) It can be observed from the given that in the first small loop, two resistors of resistane $1 Ω$ each are connected in series.
Hence, their equivalent resistance $= (1 + 1) = 2 Ω$
It can also be observed that two resistors of resistance $2 Ω$ each are connected in series. Hence, their equivalent resistance $= (2 + 2) = 4 Ω$
Therefore, the circuit can be redrawn as

It can be observed that $2 Ω and 4 Ω$ resistors are connected in parallel in all the four loops. Hence equivalent resistance (R) of each loop is given by
$R = \frac{2 \times 4}{2 + 4} = \frac{8}{6} = \frac{4}{3} Ω$
The circuit reduces to,

All the four resistors are connected in series.
Hence, equilvalent resistance of the given circuit is $\frac{4}{3} \times 4 = \frac{16}{3} Ω$
(b) It can be observed from the given circuit that five resistors of resistance R each are connected in series.
Hence, equivalent resistance of the circuit $= R + R + R + R + R = 5 R$ .

Updated on:21/07/2023

If you are provided three resistance $2 Ω, 3 Ω$ and $6 Ω$ . How will you connect them so as to obtain the equivalent resistance of $4 Ω$
A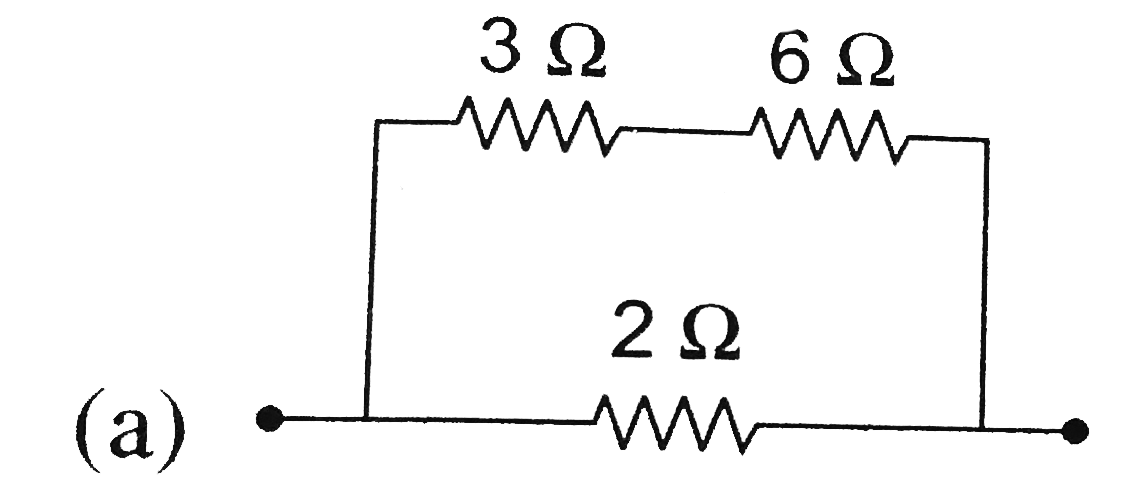
B
C
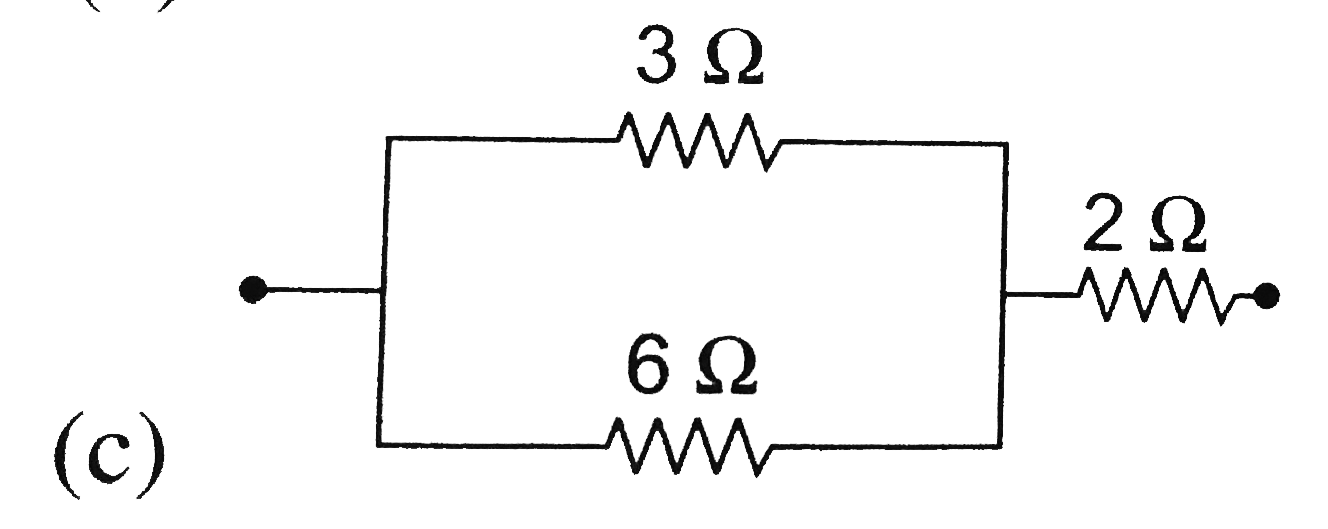Dnone
If you are provided three resistances $2 Ω, 3 Ω$ and $6 Ω$ . How will you connect then so as to obtain the equivalent resistance of $4 Ω$ ?
A
B
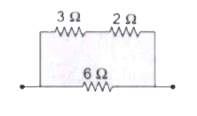C
Dnone of these