A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs. 17.50 per package on nuts and Rs. 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machines for at the most 12 hours a day?
Let the manufacturer produces x packets of nuts and y packets of bolts, then
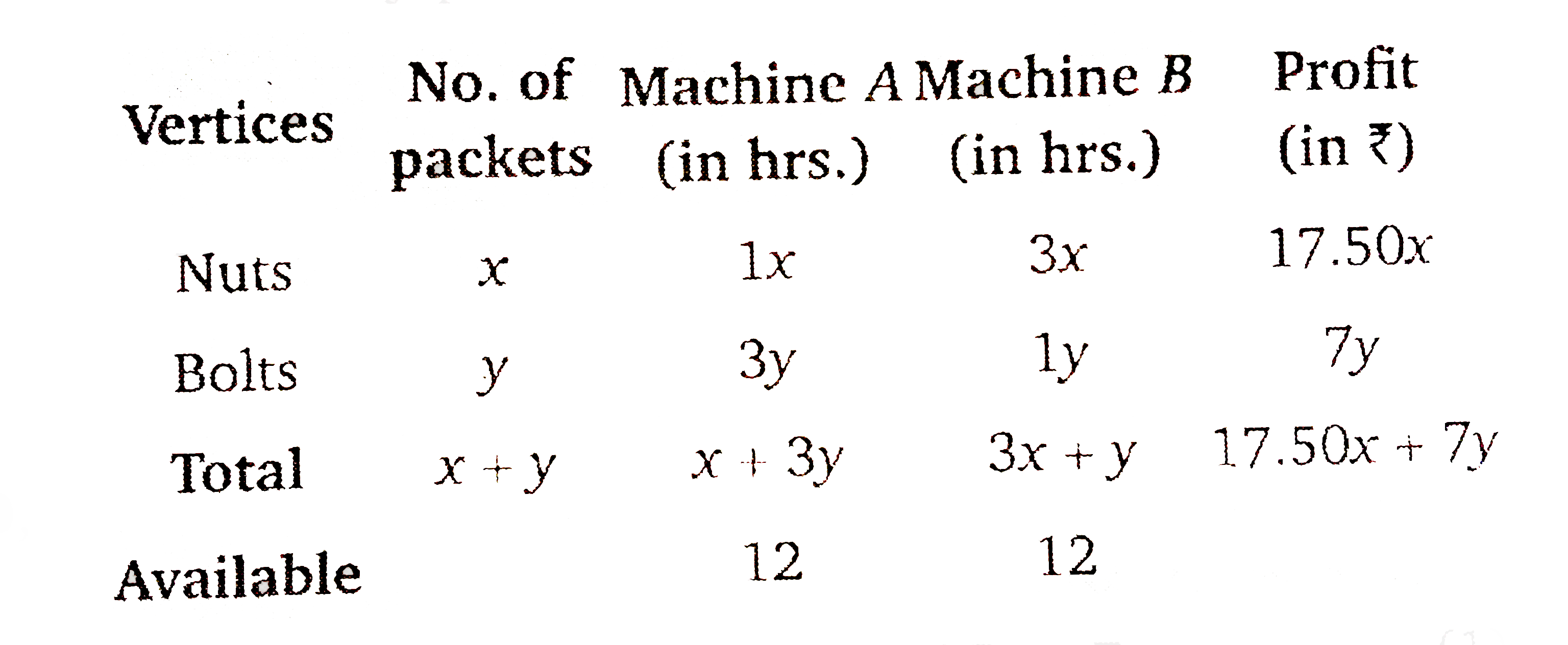
∴ Maximise Z=17.5x+7y……………….1
and constraints x+3y≤12………………………2
3x+y≤12………………….3
x≥0,y≥0………………...4

First draw the graph of the line x+3y=12.
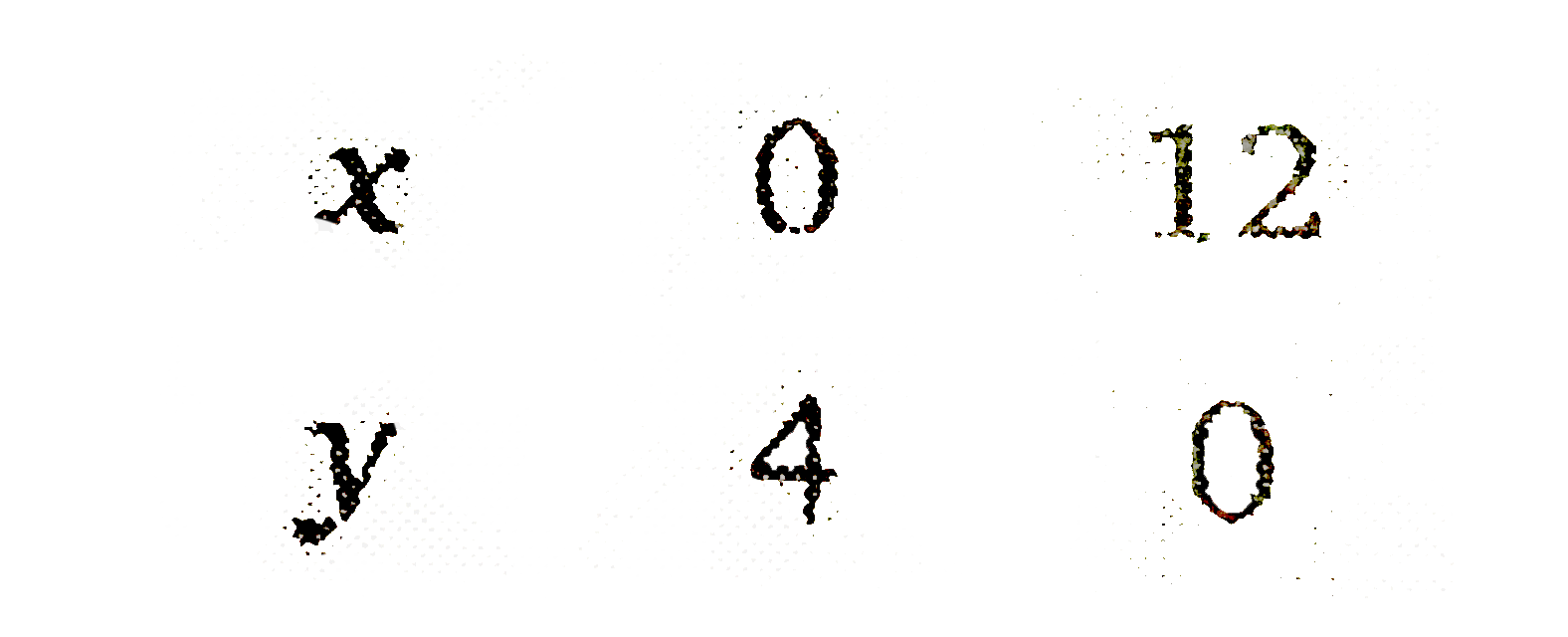
Put (0,0) in the inequation x+3y≥12 ,
0+3×0≤10⇒0≤12 (True)
Therefore half plane contains the origin. Since x,y≥0. So the feasible region is in first quadrant,
Now draw the graph of the line 3x+y=12
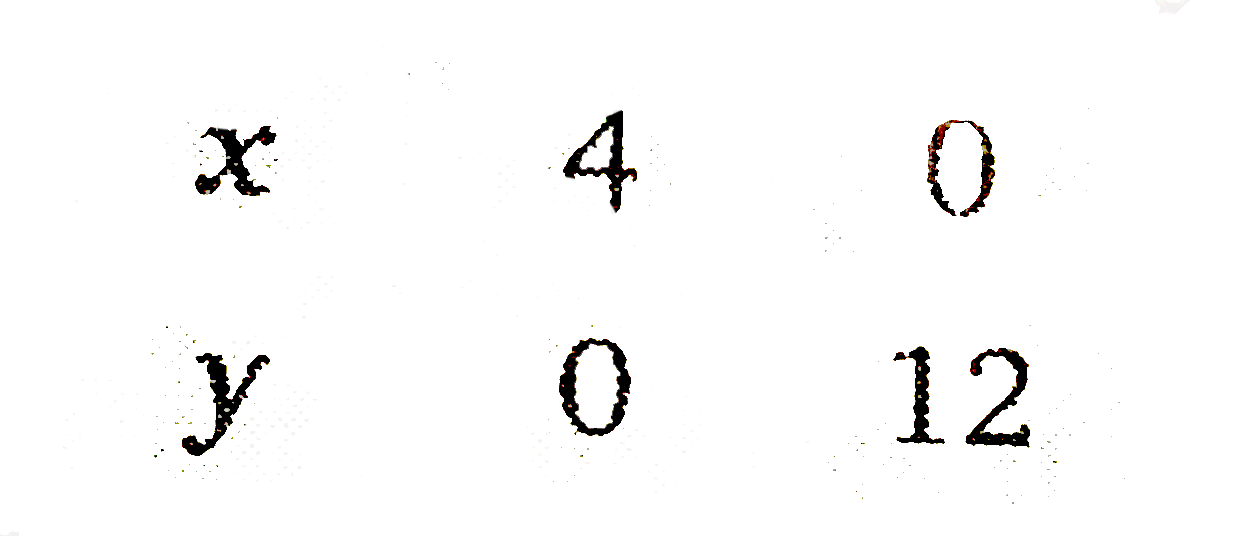
Put (0,0) in the inequation 3x+y≤12,
3×0+0≤12>0≤12 (True)
Therefore, the half plane contains the origin.
From the equations x+3y=12 and 3x+y=12, the point of intersection is B(3,3).
∴ The feasible region is OABCO whose vertices are O(0,0),A(4,0),B(3,3) and C(0,4). Now, we find the value of Z at these points,
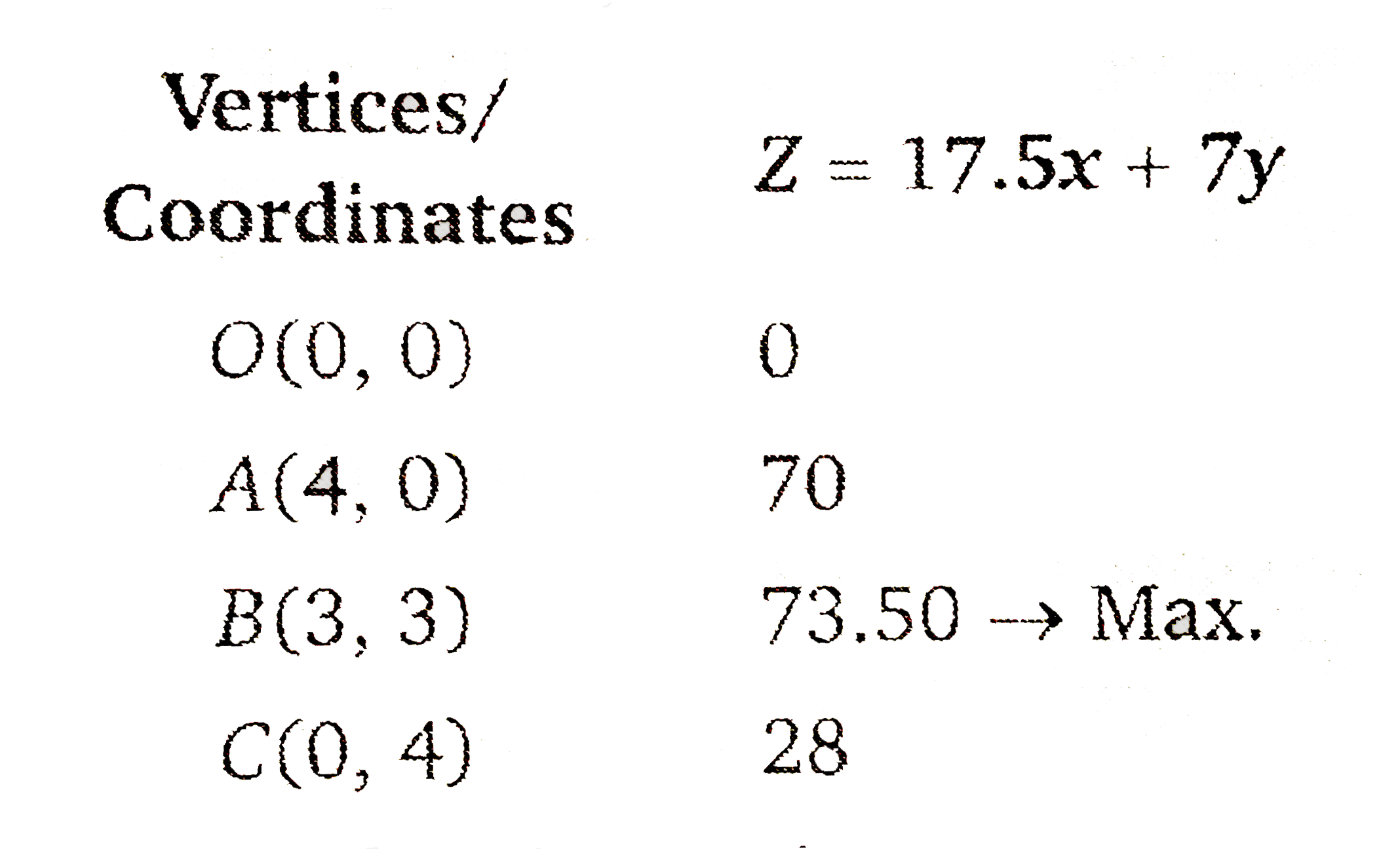
The value of Z is maximum Rs. 73.50 at point (3,3). Therefore, the maximum profit of Rs. 73.50 can be obtained when 3 packets of nuts and 3 packets of bolts are produced per day.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBook:NAGEEN PRAKASHANChapter:LINEAR PROGRAMMINGExercise:Miscellaneous Exercise
Explore 9 Videos
- LINEAR PROGRAMMINGBook:NAGEEN PRAKASHANChapter:LINEAR PROGRAMMINGExercise:Exercise 12.1
Explore 10 Videos
- INVERES TRIGONOMETRIC FUNCTIONSBook:NAGEEN PRAKASHANChapter:INVERES TRIGONOMETRIC FUNCTIONSExercise:Miscellaneous Exercise (prove That )
Explore 9 Videos
- MATRICESBook:NAGEEN PRAKASHANChapter:MATRICESExercise:Miscellaneous Exerice
Explore 15 Videos
Similar Questions
A manufacturer produces nuts and bolts. It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts. He earns a profit of Rs 17.50 per package on nuts and Rs 7.00 per package on bolts. How many packages of each should be produced each day so as to maximise his profit, if he operates his machine for at most 12 hours a day?
View Solution(i) A manufacturer produces nuts and bolts.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts while it takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts.He earns a profit og ₹ 17.50 per package of nuts and ₹ 7.00 per package of bolts.How many packages of each should be produced each day so as to maiximise his profit, if he operate his machine for at the most 12 hous a day?Form an LPP for the problem and solve it graphically.
(ii) A manufacturer produces nuts and bolts.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on amchine A and 1 hour on machine B to produce a package of bolts.He earns a profit ₹35 per package of nuts and ₹14 per package of bolts.How many packages of each should be produced each day so as to maximise his profit, if he operates each machine for atmost 12 hours a day?
View SolutionA manufacturer produces nuts and bolts. It takes 2 hours work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 2 hours on machine B to produce a package of bolts. He earns a profit of Rs. 24 per package on nuts and Rs. 18 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 10 hours a day. Make an L.P.P. from above and solve it graphically ?
View SolutionA manufacturer produces nuts and bolts. It takes 2 hours work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on machine A and 2 hours on machine B to produce a package of bolts. He earns a profit of Rs. 24 per package on nuts and Rs. 18 per package on bolts. How many packages of each should be produced each day so as to maximize his profit, if he operates his machines for at the most 10 hours a day. Make an L.P.P. from above and solve it graphically ?
View Solution(i) A manufacturer produces nuts and bolts for industrial machinery.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts while it takes 3 hours on machine A and 1 hour on machine B to produce a package of bolts.He earns a profit og ₹ 17.50 per package of nuts and ₹ 7.00 per package of bolts.How many packages of each should be produced each day so as to maiximise his profit, if he operate his machine for at the most 12 hous a day?Form an LPP for the problem and solve it graphically.
(ii) A manufacturer produces nuts and bolts.It takes 1 hour of work on machine A and 3 hours on machine B to produce a package of nuts. It takes 3 hours on amchine A and 1 hour on machine B to produce a package of bolts.He earns a profit ₹35 per package of nuts and ₹14 per package of bolts.How many packages of each should be produced each day so as to maximise his profit, if he operates each machine for atmost 12 hours a day? Convert it into an LPP and solve graphically.
View SolutionA manufacturer produces pend and pencils. It takes 1 hour of work on machine A and 2 hours on machine B to produce a package of pens while it take 2 hours on machine A and 1 hour on machine B to produce a package of pencils . He earn a profit of Rs. 4.00 per package on pens and Rs. 3.00 per package on pencils. How many packages of each should be produce each day so as to maximize his profit, if he operates his machines for at most 12 hours a day ? Formulate the above information mathematically and then solve.
View SolutionA manufacture produceds two types of steel trunks. He has two machines, A and B. The first type of book case requires 3 hours on machine A and 3 hours on machine B for completion whereas the second type required 3 hours on machine A and 2 hours n machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs.30 and Rs.25 per trunk of the first type and second type respectively. How many trunks of each type must he make each day to make the maximum profit?
View SolutionA manufacturer produces two types of steel trunks. He has tow machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 and Rs. 25 per trunk of the first type and the second respectively. How many trunks of each type must he make each day to makes maximum profit?
View SolutionManufacturer produces two types of steel trunks. He has two machines, A and B. The first type of trunk requires 3 hours on machine A and 3 hours on machine B. The second type requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs. 30 per trunk on the first type of trunk and Rs. 25 per trunk on the second type. Formulate a linear programming problem to find out how many trunks of each type he must make each day to maximize his profit.
View SolutionA factory manufactures two types of screws, A and B. Each type of screw requires the use of two machines, an automatic and a hand operated. It takes 4 minutes on the automatic and 6 minutes on hand operated machines to manufacture a package on screws A, while it takes 6 minutes on automatic and 3 minutes on the hand operated machines to manufacturer a package of screws B. Each machine is available for at the most 4 hours on any day. The manufacturer can sell a package of screws A at a profit of Rs. 7 and screws B at a profit of Rs. 10. Assuming that he can sell all the screws he manufactures, how many packages of each type should the factory owner produce in a day order to maximise his profit? Determine the maximum profit.
View Solution

