The perpendicular from the origin to a line meets it at the point (-2, 9) find the equation of the line.
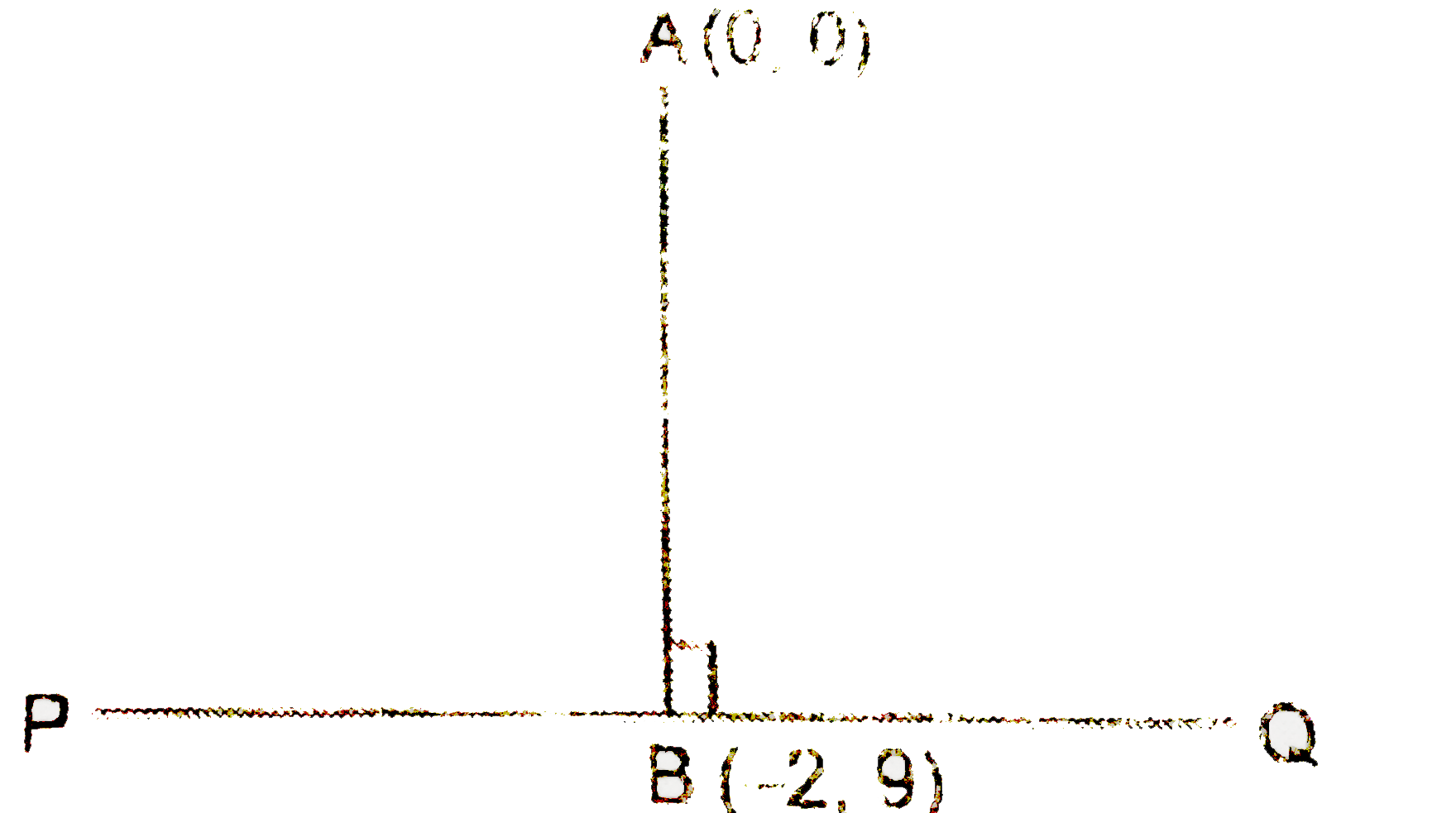
Slope of AB, m1=9−0−2−0=−92
Let slope of PQ is m2.
∴m1m2=−1
⇒m2=29
Equation of line PQ is
y−9=29(x+2)
⇒9y−81=2x+4
⇒2x−9y+85=0
Topper's Solved these Questions
- STRAIGHT LINESBOOK - NAGEEN PRAKASHANCHAPTER - STRAIGHT LINESEXERCISE - Exercise
206 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE
7 Videos
- TRIGNOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHANCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE
10 Videos
Similar Questions
Knowledge Check
The perpendicular from the origin to a line L meets it at the point (3,−9), equation of the line L is
Ax−3y=30B3x−y=18Cx+3y+24=0D3x+y=18
The perpendicular from the origin to the line y=mx+c meets it at the point (−1,2). Find the values of m and c.
View SolutionThe perpendicular from the origin to the line y=mx+c meets it at the point (-1,2). Find the values of m and c.
View SolutionIf the foot of the perpendicular from the origin to a straight line is at (3,−4) , then find the equation of the line.
View SolutionThe perpendicular from the origin to the line y=mx+c meets it at the point (−1,2). Find the values of m and c.
View Solution(i) Find the co-ordinates of the foot of perpendicular from point (−1,3) to the line 3x−4y=16.
(ii) The co-ordinates of the foot of perpendicular drawn from origin to a line are (2,3). Find the equation of the line.
View SolutionFind the equation of the line which is at a distance 5 from the origin and the perpendicular from the origin to the line makes an angle 600 with thepositive direction of the x-axis.
View SolutionThe length of the perpendicular segment from the origin to a line is 2 units and the inclination of this perpendicular is α such that sin α=13andα is acute. Find the equation of the line.
View Solution
