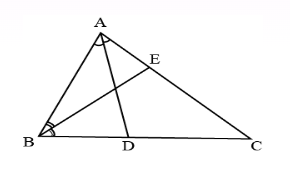
ABC is a triangle in which ∠B =2 ∠C.D is a point on BC such that AD bisects ∠BAC and AB=CD . Prove that ∠BAC=720.
Let BP be the bisector of ∠ABC. Join PD.
Let ∠BAD=∠DAC=x
Let ∠ABP=∠PBC=y
Also ∠B=2∠C
⇒ 2y=2∠C
⇒ ∠C=y
Since ∠PBD=∠PCD=y
⇒ PB=PC ...(I) (sides opposite to equal angles are equal)
Now, in ΔABP and ΔDCP
∵⎧⎪⎨⎪⎩AB=DC(given)∠ABP=∠DCP(each equal to y)PB=PC[from (1)]
∴ΔABP≅ΔDCP (SAS)
∴∠BAP=∠CDP (c.p.c.t)
⇒ ∠CDP=2x and AP=DP (c.p.c.t)
∴∠PDA=∠PAD=x
For ΔABD,∠ADC is the exterior angle
∴∠CDP+∠ADP=x+2y (ext. ∠th.)
⇒ 2x+x=x+2y ⇒ x=y
Now, in ΔABC,
∠A+∠B+∠C=180∘ (angle sum property)
⇒ 2x+2y+y=180∘
⇒ 2x+2x+x=180∘ (∵x=y)
⇒ 5x=180∘ ⇒ x=36∘
⇒ ∠BAC=2x=72∘ Hence Proved.

Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHANCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
In Figure, ABC is a triangle in which ∠B=2∠C . D is a point on side BC such that AD bisects ∠BAC and AB=CD.BE is the bisector of ∠B . The measure of ∠BAC is
(a) 720
(b) 730
(c) 740
(d) 960
View SolutionABC is a triangle in which ∠B =2 ∠C.D is a point on BC such that AD bisects ∠BAC and AB=CD . Prove that ∠BAC=720.
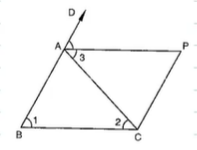
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.
View SolutionABC is a triangle. D is a point on AB such that D=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC
View SolutionIn Figure, it is given that AB=BC and AD=EC . Prove that ABE≅CBD
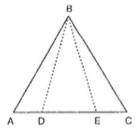
View SolutionABC is a triangle. D is a point on AB such that AD=14AB and E is a point on AC such that AE=14AC. Prove that DE=14BC.
View SolutionIn a parallelogram ABCD, the bisector of ∠A also bisects BC at X Prove that AD=2AB
View SolutionIn a scalene triangle ABC,D is a point on the side AB such that CD2=ADDB, sin s∈AS∈B=sin2C2 then prove that CD is internal bisector of ∠C.
View SolutionABCD is a trapezium with ABDC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionIf ABC is an isosceles triangle such that AB=AC and AD is an altitude from A on BC . Prove that (i) ∠B=∠C (ii) AD bisects BC (iii) AD bisects ∠A
View Solution
