Find the missing frequency in the following distribution if N is 60 and median is 40.
Video Solution
Text Solution
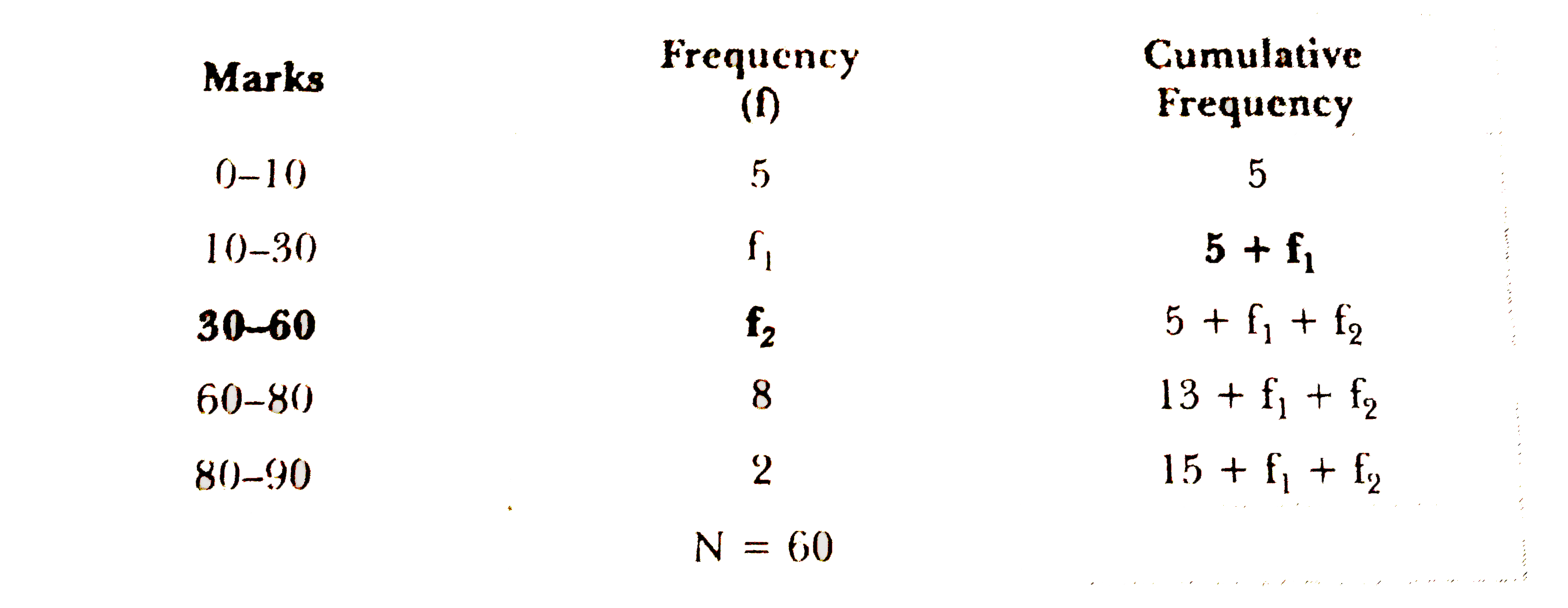
∴N=60
∴15+f1+f2=60orf1+f2=45
Median Size =N2=602=30th term
(∴ Median is 40 , so Median class is 30-60)
M=l1+N2−c.f.f×i
⇒40=30+30−(5+f1)f2×30
⇒10=(25−f1)f2×30
⇒10f2=750−30f1
30f1+10f2=750
Thus, we get
f1+f2=45 ... (i)
30f1+10f2=750 ...(ii)
Dividing equation (ii) by 10, we get
3f1+f2=75 ... (iii)
Now subtracting (i) from (iii), we get
3f1+f2=75
f1−+−f2=45−2f1=30
⇒f1=15
Now substituting f1=15 in (i) , we get
f2=45−15=30
Hence , f1=15,f2=30.
|
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY MEDIAN AND MODEBook:TARUN JAIN & VK OHRIChapter:MEASURES OF CENTRAL TENDENCY MEDIAN AND MODEExercise:Miscellaneous Illustrations
Explore 30 Videos
- MEASURES OF CENTRAL TENDENCY MEDIAN AND MODEBook:TARUN JAIN & VK OHRIChapter:MEASURES OF CENTRAL TENDENCY MEDIAN AND MODEExercise:Objective Type Questios
Explore 26 Videos
- MEASURES OF CENTRAL TENDENCY - ARITHMETIC MEANBook:TARUN JAIN & VK OHRIChapter:MEASURES OF CENTRAL TENDENCY - ARITHMETIC MEANExercise:Illustration
Explore 72 Videos
- MEASURES OF DISPERSIONBook:TARUN JAIN & VK OHRIChapter:MEASURES OF DISPERSIONExercise:Learning by doing
Explore 30 Videos
Similar Questions
Knowledge Check
Find the missing frequency in the following distribution, if it is known that the mean of the distribution is 50.16
 Af1= 27Bf1= 23Cf1 = 34Df1 = 30
Af1= 27Bf1= 23Cf1 = 34Df1 = 30
Find the missing frequency (o) for the following distribution, whose mean is 7.77
View SolutionFind the missing frequency in the following distribution if N=100 and M=30.
Marks0−1010−2020−3030−4040−5050−60Number of Students 10 ? 25 30 ? 10
View SolutionFind the median of the following distribution
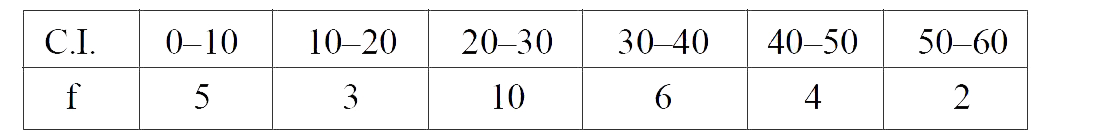
View SolutionFind the median of the following distribution
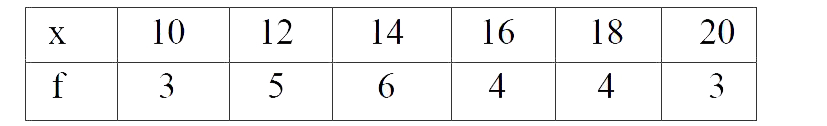
View SolutionFind the missing frequencies in the following frequecny distribution table, if N=100 and median is the value of √1056−√1056−√1056−√1056...∞

View SolutionFind the mean and median of the following distribution :
View SolutionFind the median for the following frequency distribution:
View Solution

