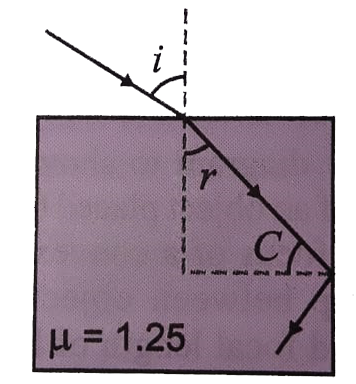
Given a slab with index n=1.33 and incident light striking the top horizontal face at angle i as shown in figure. The maximum value of i for which total internal reflection occurs is

sin−1(√0.77)
cos−1(√0.77)
sin−1(0.77)
sin−1(0.38)
The correct Answer is:A
(a) TIR to take place ,
902−r>θC
⇒r>90∘−θC
From the relation,
μ=sinisinr
sini=μsinr
Since, for TIR to take place,r<90∘−θC
∴i=sin−1{μsinr}
i≤sin−1[{nsin(90∘−θC)}]
or i≤sin−1{μcosθC}
or i≤sin−1{μ√1−1μ2}(∵sinθC=1μC)
or i≤sin−1⎧⎨⎩1.33√1−1(1.33)2⎫⎬⎭
or i≤sin−1{√0.77}

Topper's Solved these Questions
- RAY OPTICSBook:DC PANDEYChapter:RAY OPTICSExercise:medical entrance special format question
Explore 25 Videos
- RAY OPTICSBook:DC PANDEYChapter:RAY OPTICSExercise:Medical entrance gallary
Explore 76 Videos
- RAY OPTICSBook:DC PANDEYChapter:RAY OPTICSExercise:Checkpoint 9.7
Explore 10 Videos
- NUCLEIBook:DC PANDEYChapter:NUCLEIExercise:C MADICAL ENTRANCES GALLERY
Explore 46 Videos
- REFLECTION OF LIGHTBook:DC PANDEYChapter:REFLECTION OF LIGHTExercise:Subjective
Explore 9 Videos
Similar Questions
Knowledge Check
Consider the ray diagram for the refraction given Fig. The maximum value of angle θ for which the light suffers total internal reflection at the vertical surface, is.
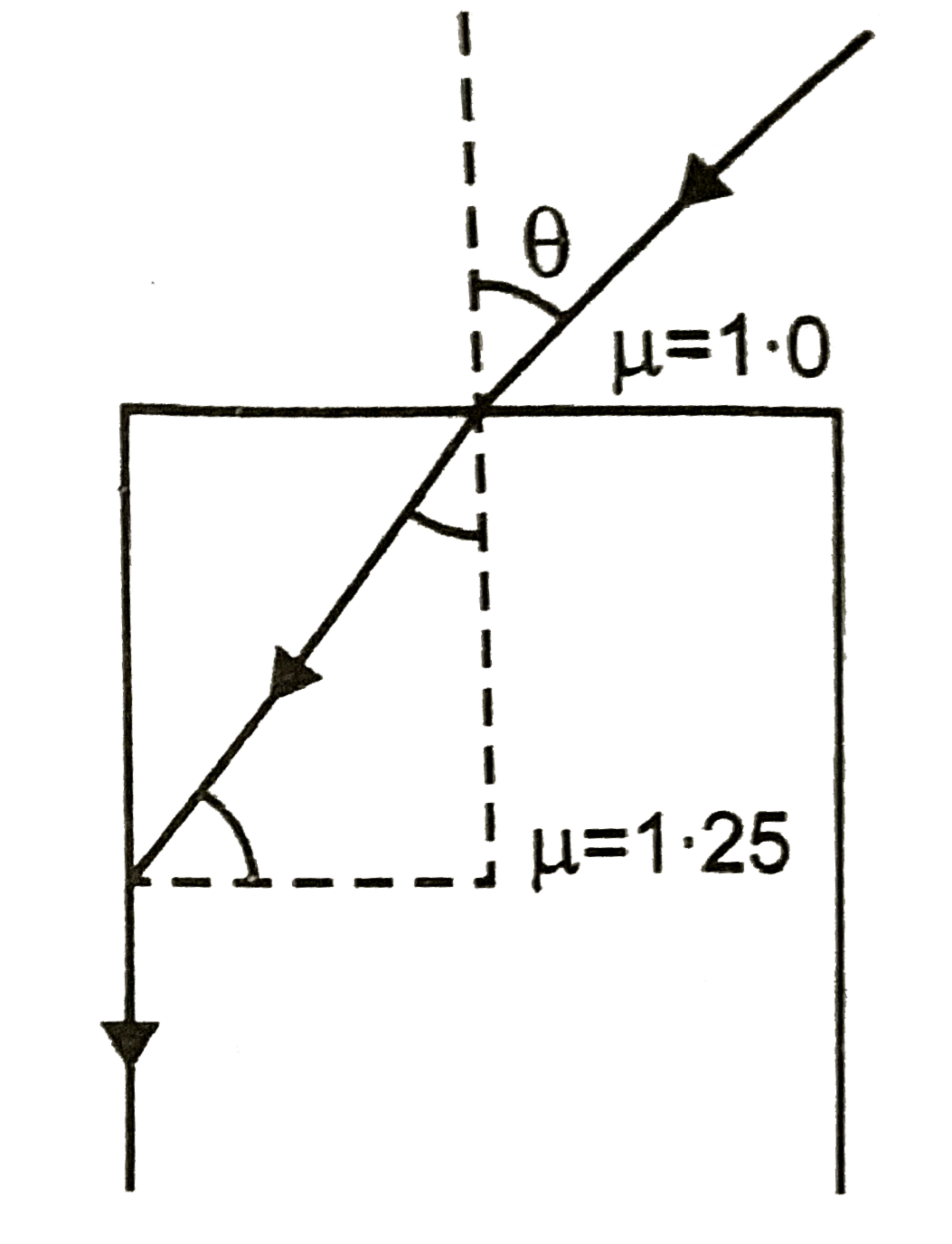 .Acos−1(34)Bsin−1(34)Ctan−1(43)Dcot−1(43)
.Acos−1(34)Bsin−1(34)Ctan−1(43)Dcot−1(43)Consider the ray diagram for the refraction given Fig. The maximum value of angle θ for which the light suffers total internal reflection at the vertical surface, is
 Acos−1(34)Bsin−1(34)Ctan−1(34)Dcot−1(34)
Acos−1(34)Bsin−1(34)Ctan−1(34)Dcot−1(34)A horizontal ray of light passes through a prism of index 1.50 and apex angle 4∘ and then strikes a vertical mirror , as shown in the figure. Through what angle must the mirror be rotated if after reflection the ray is to be horizontal?
_E01_041_Q01.png) A4∘B90.5∘C1∘D1.5∘
A4∘B90.5∘C1∘D1.5∘
A slab of refractive index μ is placed in air and light is incident at maximum angle θ0 from vertical. Find minimum value of μ for which total internal reflection takes place at the vertical surface.
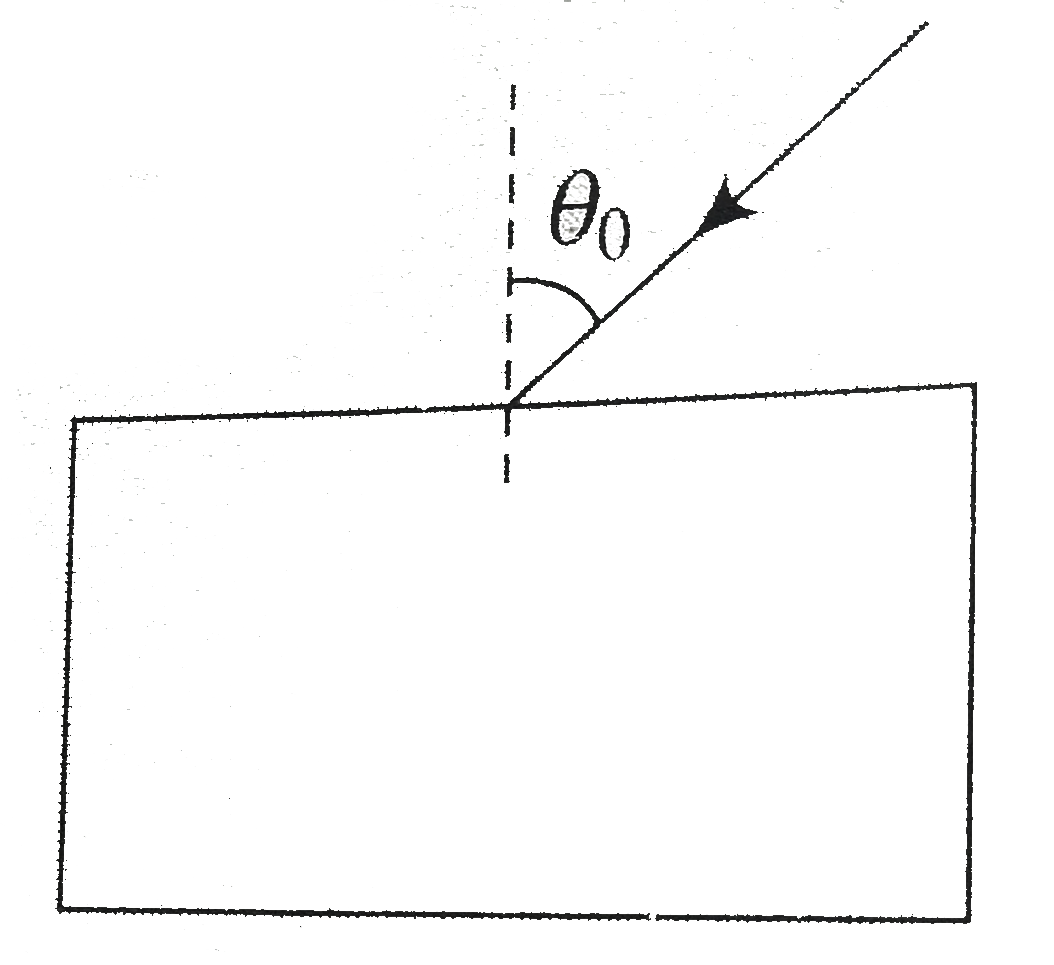
View SolutionConsider the situation shown in figure. Find the maximum angle theta for which the light suffers total internal reflection at the vertical surface.
View SolutionCross section of a light pipe is shown in the following figure :

Inner core is material of refractive index 1.68 and its outer covering is a material of refractive index 1.44. Find the maximum angle at which the ray can be incident with the axis of pipe for which total internal reflection occurs inside the pipe.
View SolutionIn the figure shown for an angle of incidence i at the top of the surface, what is the minimum refractive index for total internal reflection at the vertical surface.
View SolutionA ray of light is incident on the left vertical face of glass cube of refractive index n2, as shown in figure. The plane of incidence is the plane of the page, and the cube is surrounded by liquid (refractive index=n1). What is the largest angle of incidence θ1 for which total internal reflection occurs at the top surfaces?

View Solution


 .
.