A convex lens forms an image of an object on a screen 30 cm from the lens. When the lens is moved 90 cm towards the object, then the image is again formed on the screen. Then, the focal length of the lens is
13 cm
24 cm
33 cm
40 cm
The correct Answer is:B
To solve the problem step by step, we will use the lens formula and the information provided in the question.
Step 1: Understand the situation
We have a convex lens that forms an image at a distance of 30 cm from the lens. When the lens is moved 90 cm towards the object, the image is still formed on the screen. We need to find the focal length of the lens.
Step 2: Set up the lens formula
The lens formula is given by:
1f=1v−1u
where:
- f = focal length of the lens
- v = image distance from the lens
- u = object distance from the lens
Step 3: Analyze the first condition
In the first scenario, the image is formed at 30 cm from the lens, so:
- v=30 cm
- Let u be the object distance (which we need to find).
Using the lens formula:
1f=130−1u(Equation 1)
Step 4: Analyze the second condition
When the lens is moved 90 cm towards the object, the new object distance becomes u−90 cm (since the lens is moving closer to the object). The new image distance is now v1=30+90=120 cm (the image remains on the screen).
Using the lens formula again:
1f=1120−1(u−90)(Equation 2)
Step 5: Equate the two equations
From Equation 1:
1f=130+1u
From Equation 2:
1f=1120+1(u−90)
Since both equations equal 1f, we can set them equal to each other:
130+1u=1120+1(u−90)
Step 6: Solve for u
Cross-multiplying to eliminate the fractions:
1u−1(u−90)=1120−130
Finding a common denominator for the left side:
(u−90)−uu(u−90)=1120−4120
−90u(u−90)=−3120
Cross-multiplying gives:
90×120=3u(u−90)
10800=3u2−270u
3u2−270u−10800=0
Dividing the entire equation by 3:
u2−90u−3600=0
Step 7: Use the quadratic formula
Using the quadratic formula u=−b±√b2−4ac2a:
u=90±√(−90)2−4⋅1⋅(−3600)2⋅1
u=90±√8100+144002
u=90±√225002
u=90±1502
Calculating the two possible values:
1. u=2402=120 cm (valid)
2. u=−602=−30 cm (not valid)
Step 8: Substitute u back to find f
Now substituting u=120 cm back into Equation 1:
1f=130+1120
Finding a common denominator (120):
1f=4120+1120=5120
Thus:
f=1205=24 cm
Final Answer
The focal length of the lens is 24cm.
---
We have a convex lens that forms an image at a distance of 30 cm from the lens. When the lens is moved 90 cm towards the object, the image is still formed on the screen. We need to find the focal length of the lens.
The lens formula is given by:
1f=1v−1u
where:
- f = focal length of the lens
- v = image distance from the lens
- u = object distance from the lens
In the first scenario, the image is formed at 30 cm from the lens, so:
- v=30 cm
- Let u be the object distance (which we need to find).
1f=130−1u(Equation 1)
When the lens is moved 90 cm towards the object, the new object distance becomes u−90 cm (since the lens is moving closer to the object). The new image distance is now v1=30+90=120 cm (the image remains on the screen).
1f=1120−1(u−90)(Equation 2)
From Equation 1:
1f=130+1u
From Equation 2:
1f=1120+1(u−90)
130+1u=1120+1(u−90)
Cross-multiplying to eliminate the fractions:
1u−1(u−90)=1120−130
(u−90)−uu(u−90)=1120−4120
−90u(u−90)=−3120
90×120=3u(u−90)
10800=3u2−270u
3u2−270u−10800=0
Dividing the entire equation by 3:
u2−90u−3600=0
Using the quadratic formula u=−b±√b2−4ac2a:
u=90±√(−90)2−4⋅1⋅(−3600)2⋅1
u=90±√8100+144002
u=90±√225002
u=90±1502
Calculating the two possible values:
1. u=2402=120 cm (valid)
2. u=−602=−30 cm (not valid)
Now substituting u=120 cm back into Equation 1:
1f=130+1120
Finding a common denominator (120):
1f=4120+1120=5120
Thus:
f=1205=24 cm
The focal length of the lens is 24cm.
Topper's Solved these Questions
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - medical entrance special format question
25 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Medical entrance gallary
76 Videos
- RAY OPTICSBOOK - DC PANDEYCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.7
10 Videos
- NUCLEIBOOK - DC PANDEYCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY
46 Videos
- REFLECTION OF LIGHTBOOK - DC PANDEYCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
Similar Questions
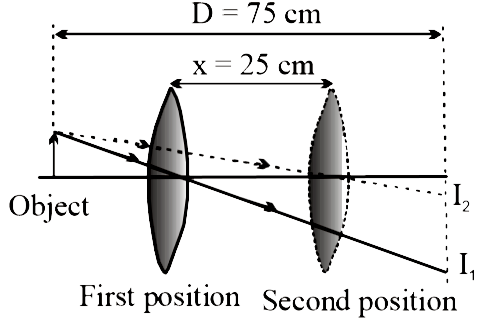
A convex lens when placed in the first position forms a real image of an object on a fixed screen. The distance between the object and the screen is 75 cm. On displacing the lens from first position by 25 cm to the second position, again a real image is formed on the screen. Then the focal length of the lens is
View SolutionA convex lens forms a blurred image of an object on a screen.
Suggest a suitable way to get a sharp image on a screen without disturbing the object , lens or the screen.
View Solution
Knowledge Check
A convex lens produces an image of a real object on a screen with a magnification of 1/2. When the lens is moved 30 cm away from the object, the magnification of the image on the screen is 2. The focal length of the lens is
A30 cmB60 cmC20 cmD15 cmA convex lens forms a real image on a screen placed at a distance 60 cm from the object. When the lens is shifted towards the screen by 20 cm , another image of the object is formed on the screen. The focal length of the lens is :
A45cmB40/3cmC30cmD12cmA convex lens forms an image of an object on a screen. The height of the image is 9 cm . The lens is now displaced until an image is again obtained on the screen. Then height of this image is 4 cm . The distance between the object and the screen is 90 cm.
AThe distance between the two positions of the lens is 30 cmBThe distance of the object from the lens in its first position is 36 cmCThe height of the object is 6 cmDThe focal length of the lens is 21.6 cm
A convex lens forms a real and inverted image of a pencial at a distance of 60 cm from the lens. The image formed is of the same size as the object. Find the focal length and power of the lens. At what distance is the pencil placed from the lens. ?
View SolutionAn object and a screen are mounted on an optical bench and a converging lens is placed between them so that a sharp image is obtained on the screen. The linear magnification of the image is 25. The lens is now moved 30 cm towards the screen and a sharp image is ■ again formed on the screen. Find the focal length of the lens
View SolutionAn object to the left of a lens is imaged by the lens on a screen 30cm to the right of the lens. When the lens is moved 5cm to the right, the screen must be moved 5cm to the left to refocus the images. The focal length of lens is :-
View SolutionA convex lens is used to form image of an object on screen. When half of the lens is covered by painting black on it, then
View SolutionA convex lens forms an image of an object on a screen ,The height of the image is9cmThe lens is now disiplaced between the object on the screen.the height of this image is4cm.the distance between the object and the screen is 90cm
View Solution