A series circuit consisting of an inductance $-$ free resistance $R = 0.16 k Ω$ and coil with active resistance is connected to the mains with effective voltabe $V = 220 V$ . Find the heat power generated in the coil if the effective voltage values across the resistance $R$ and the coil are equal to $V_{1} = 80 V$ and $V_{2} = 180 V$ respectively.

Video Solution

Text Solution

Verified by Experts

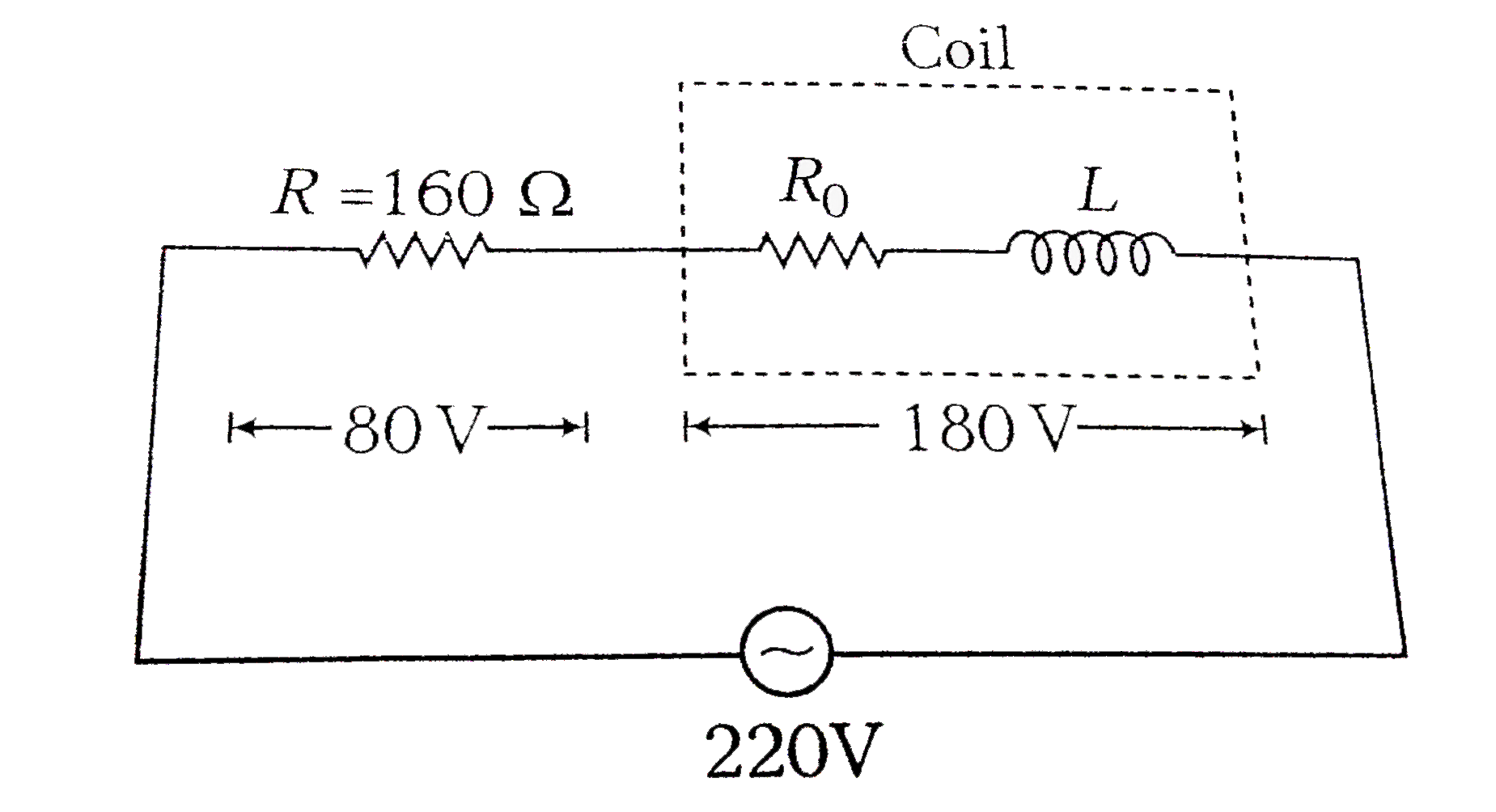
Current in the circuit,
$V_{r} = I_{r m s} R$
$\Rightarrow 80 = I_{r m s} \times 160 \Rightarrow I_{r m s} = \frac{1}{2} A$
Now, $V_{R 0} = I_{r m s} R_{R_{0}} = \frac{R_{0}}{2}$
and $V_{L} = I_{r m s} R_{0} = \frac{R_{0}}{2}$
$\Rightarrow (V_{R} + V_{R 0}^{2} + V_{L}^{2} = {(220)}^{2}$
$\Rightarrow {(80 + \frac{R_{0}}{2})}^{2} + \frac{X_{L}}{2^{2}} = {(220)}^{2}$
Also, $V_{R 0}^{2} + V_{L}^{2} = {(180)}^{2}$
$\Rightarrow \frac{R_{0}}{{(2)}^{2}} + {(\frac{X_{L}}{2})}^{2} = {(180)}^{2}$
Subtracting Eqs. (i) and (ii), we get
$\frac{80 + R_{0}}{2})^{2} - {(\frac{R_{0}}{2})}^{2} = {(220)}^{2} - {(180)}^{2}$
$\Rightarrow (80 + R_{0}) (80) = (400) (40)$
Power consumed in coil,
$P = I_{r m s}^{2} R_{0} = {(\frac{1}{2})}^{2} \times 120 = 30 W$

Updated on:21/07/2023

A 100 V voltmeter of internal resistance 20 $k ω$ is in series with a high resistance R, is connected to 110 V line . The voltmeter reads 5 V, then the value of R is
A $210 k Ω$
B $315 k Ω$
C $420 k Ω$
D $4440 k Ω$
A 100 V voltmeter of internal resistance $20 k Ω$ n series with a high resistance R is connected to 110 V line. The voltmeter reads 5V, the value of R is -
A $210 k Ω$
B $315 k Ω$
C $420 k Ω$
D $4440 k Ω$
A $100 V$ voltmeter of internal resistance $20 k Ω$ in series with a high resistance $R$ is connected to a $110 V$ line. The voltmeter reads $5 V$ , the value of $R$ is
A $210 Ω$
B $315 Ω$
C $420 Ω$
D $400 Ω$