A coil with active resistance R and inductance L was connected at the moment t=0 to a source of voltage V=Vmcosωt. Find the current in the coil as a function of time t.
The equatio of the circuit is (I is the current )
LdIdt=RI=Vmcosωt
From the theory of different equations.
I=Ip+IC
where Ip is a particular integral and IC is the complementary function ( Solution of the differential equation with the RHS =0).Now
IC=ICOe−tR/L
and for Ip we write Ip=Imcos(ωt−φ)
Substituting we get
Im=Vm√R2+ω2L2,φ=tan−1(ωL)R
Then Im=Vm√R2+ω2L2cos(ωt−φ)+ICOe−tR/L
Now in an inductive circuit I=0 at t=0
because a current cannot change suddently.
Thus ICO=−Vm√R2=ω2L2cosφ
and so I=Vm√R2+ω2L2[cos(ωt−φ)−cosφe−tR/L]
Topper's Solved these Questions
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Elastic Waves39videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OSCILLATIONS AND WAVESEXERCISE - Electromagnetic Waves, Radiation36videos
OSCILLATIONS AND WAVES
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - OPTICSEXERCISE - Exercise2videos
OPTICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - PHYSICAL FUNDAMENTALS OF MECHANICSEXERCISE - Relativistic Mechanics49videos
PHYSICAL FUNDAMENTALS OF MECHANICS
Similar Questions
A circuit consisting of a capacitor with capacitance C and a resistance R connected in series was connected at the moment t=0 to a source of ac voltage V=Vmcosωt . Find the current in the circuit as a function of time t.
View SolutionA capacitor with capacitance C and a coil with active resistance R and inductance L are connected in parallel to a source of sinusoidal voltage of frequency ω. Find the phase difference between the current fed to the circuit and the source voltage.
View Solution
Knowledge Check
- Question 1 - Select One
A coil resistance R and inductance L is connected to a battery of emf E volt. The final current in the coil is
AERBELC√(ER2+L2)D√(ELR2+L2) - Question 2 - Select One
A coil of resistance R and inductance L is connected across an a.c power supply of r.m.s. voltage V. The average power dissipated in the coil is,
AV2/RBV2R(R2+ω2L2)CV2√R2+ω2L2Dzero
In the circuit shown the source voltage is given asv=V0 sin ωt. Find the current through the source as a function of time.
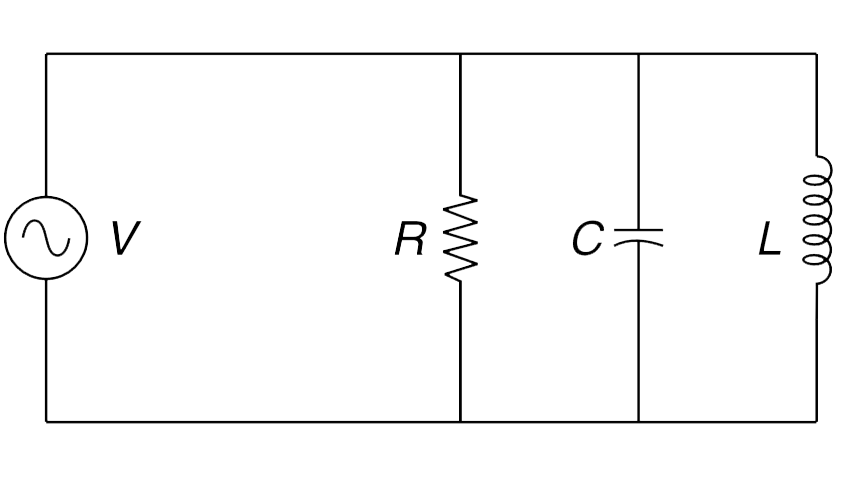 View Solution
View SolutionA series circuit consisting of a capacitor XC=80Ω and a coil with active resistance R=300Ω and inductance XL=40ω is connected to a source of alternating voltage with amplitude V0=200V Find
(a) the current amplitude in the circuit
(b) the phase difference between the current and voltage
(c) the amplitudes of voltage across the capacitor and the coli .View SolutionA capacitor with capacitance C whose interelectrode space is filled up with poorly conducting medium with active resistance R is connected to a source of alternating voltage V=Vmcosωt. Find the time dependence of the steady − state current flowing in lead wires. The resistance of the wires is to be neglected.
View SolutionA capacitor with capacitance C=1.0μF and a coil with active resitance R=0.10Ω and inductance L=1.0mH are connected in parallel to a source of sinusoidal voltage V=31V. Find :
(a) the frequency ω at which the resonance sets in ,
(b) the effective value of the fed current in resonance , as well as the corresponding currents flowing through the coil and through the capacitor.View SolutionA closed circuit consits of a source of constant and E and a choke coil of inductance L connected in series. The active resistance of the whole circuit is equal to R. At the moment t=0 the choke coil inductance was decreased abrupty η times. FInd the current in the circuit as a function of time t.
View SolutionA circuit consists of a capacitor with capacitance C and a coil of inductance L connected in series, as well as a switch and a resistance equal to the critical value for this circuit. With the switch disconnected, the capacitor was charged to a voltage V0, and at the moment t=0, the switch was closed . Find the corrent I in the circuit as a function of time t.What is Imax equal to ?
View Solution

