In a uniform magnetic field, a π shaped metal frame is located perpendicular to the plane of the conductor and varying with time at the rate (dB/dt)=0.20T/s. A conducting connector starts moving with an acceleration a=30cm/s2 along the parallel bars of the frame. The length of the connector is equal to l = 44 cm. Find the emf induced in the loop t = 1 s after the beginning of the motion, if at the moment t = 0, the loop area and the magnetic induction are equal to zero.
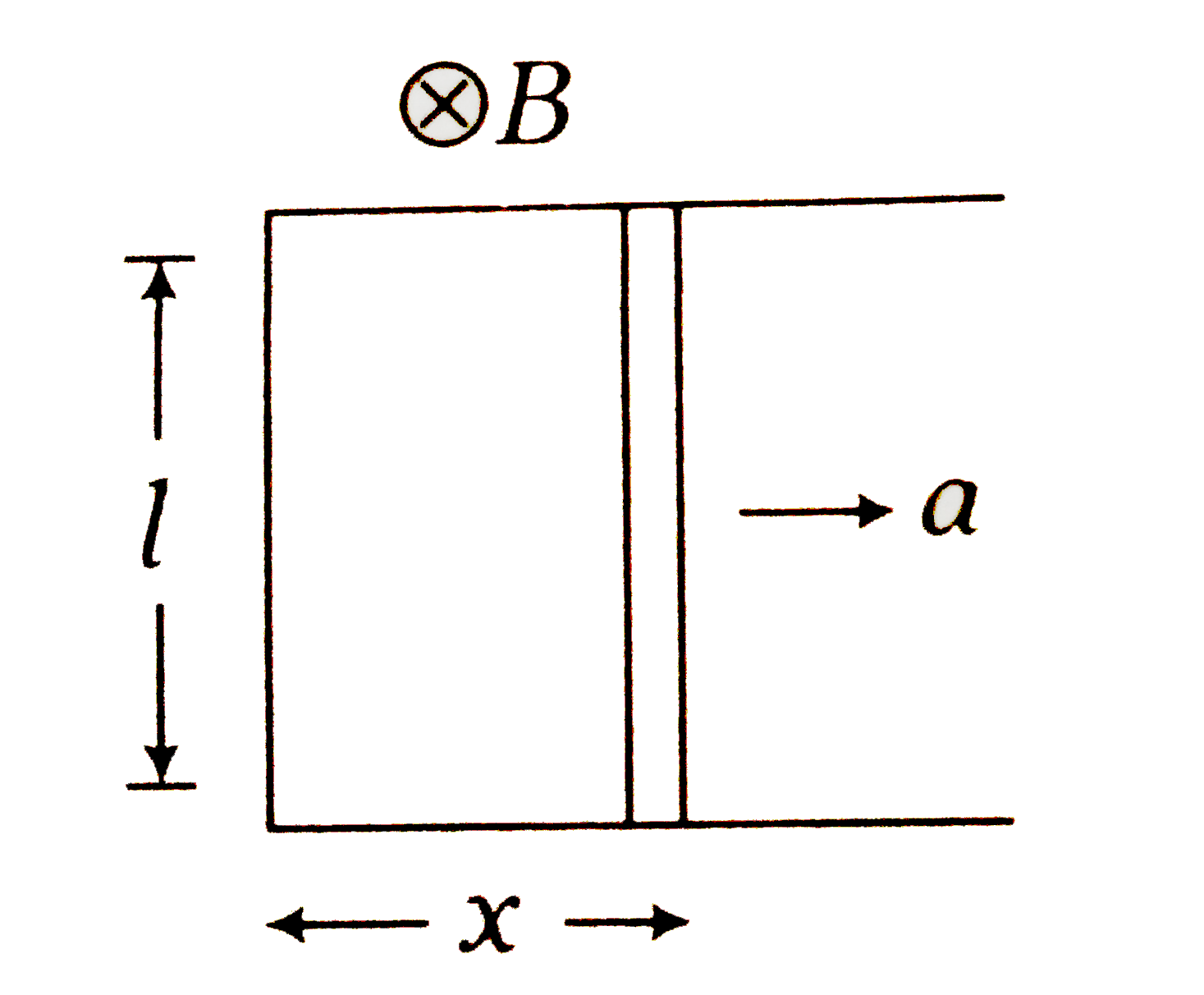
We know, according to kinematic equation, distance travelled
x=ut+12at2. Here, initial velocity, u = 0, acceleration,
a = b = 30cm/s2
So, in time t, distance travelled by conductor, x=12bt2
Flux passing through loop, ϕ=BS=Blx=Blbt22
Here, B and t both are variable.
So, induced emf, e=∣∣∣dϕdt∣∣∣=lb2[dBdtt2+B.2t]
=0.4×0.32(0.2×22+2B)
=0.06(0.8+2B)
Given, dBdt=0.2T/s⇒ dB=0.2dt
On integrating both sides, we get
∫B0dB=0.2∫t0dt⇒B=0.2t=0.2×1=0.2
So, induced emf, e=0.06(0.8+0.2)=0.06V=6×10−2V
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 1
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 2
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
A π shaped metal frame is located in a uniform magnetic field perpendicular to the plane of the conductor and varying with time at the rate (dB/dt)=0.I0T/sec . A conducting connector starts moving with an acceleration a=I0cm/sec2 along the parallel bars of the frame. The lenght o0f the connector is equal to l=20cm . Find the emf induced in the loop t=2sec after the beginnig of the motion, if at the moment t=0 the loop area and the magnetic induction are equal to zero. The inductance of the loop is to be neglected.
View SolutionA II-shaped conductor is located in a uniform magnetic field perpendicular to the plane of the conductor and varying with time at the rate dBdt=0.10T/s.A conducting connectors starts moving with a constant acceleration w=10cm/s2 along the parallel bars of the conductor.The length of the connector is equal to l=20cm.Find the emf induced (in mV) in the loop t=2.0s after the beginning of the motion.If at the moment t=0 the loop area and the magnetic induction (B) are equal to zero.The self inductance of the loop is to be neglected.
View Solution
Knowledge Check
A conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is
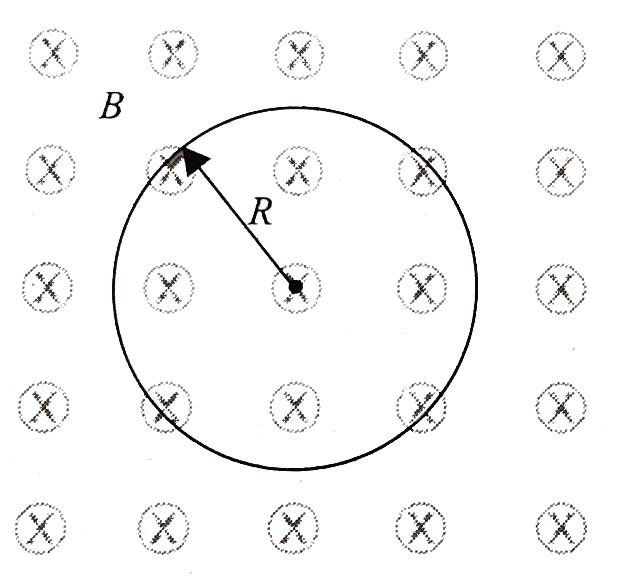 A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzero
A2π(R0+t)B clockwiseBπ(R0+t)B clockwiseC2π(R0+t)B anticlockwiseDzeroPlane figures made of thin wires of resistance R=50 milliohm//metre are located in a uniform magnetic field perpendicular into the plane of the figures and which decrease at the rate dB/dt=0.1mT/s. Then currents in the inner and outer boundary are. (The inner radius a=10cm and outer radius b=20cm)
 A10−4A(clockwise),2×10−4A(clockwise)B10−4A(Anticlockwise),2×10−4A(clockwise)C2×10−4A(clockwise),10−4A(Anticlockwise)D2×10−4A(Anticlockwise),10−4A(anticlockwise)
A10−4A(clockwise),2×10−4A(clockwise)B10−4A(Anticlockwise),2×10−4A(clockwise)C2×10−4A(clockwise),10−4A(Anticlockwise)D2×10−4A(Anticlockwise),10−4A(anticlockwise)A conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of ring. If radius R varies as a function of time t as R=R0+t2. The emf induced in the loop is
 A2πBt(R0+t2) ClockwiseB2πBt(R0+t2) AnticlockwiseC4πBt(R0+t2) AnticlockwiseD4πBt(R0+t2) Clockwise
A2πBt(R0+t2) ClockwiseB2πBt(R0+t2) AnticlockwiseC4πBt(R0+t2) AnticlockwiseD4πBt(R0+t2) Clockwise
A uniform magnetic field B exists in a direction perpendicular to the palne of a square frame made of copper wire. The wire has a total length of 40cm . The magnetic field changes with time at a steady rate (dB/dt)=0.02T/sec . Find the current induced in the frame. Resistance of wire =I0Ω
View SolutionA conducting rod of unit length moves with a velocity of 5m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.4T. Find the emf induced between the ends of the stick.
View SolutionA conducting cirular loop is placed in a unifrom transcerse magnetic field of 0.02 T . Somehow , the radius of the loop begins to decrease at a constant rate of 1. 0 mm/s . Find the emf induced in the loop at the instant when the radius is 2 cm.
View SolutionA rectangular loop with a sliding conductor of length l is located in a uniform magnetic field perpendicular to the plane of loop. The magnetic induction perpendicular to the plane of loop Is equal to B. The part ad and be has electric resistance R1 and R2, respectively. The conductor starts moving with constant acceleration a0, at time t=0. Neglecting the self-inductance of the loop and resistance of conductor. Find
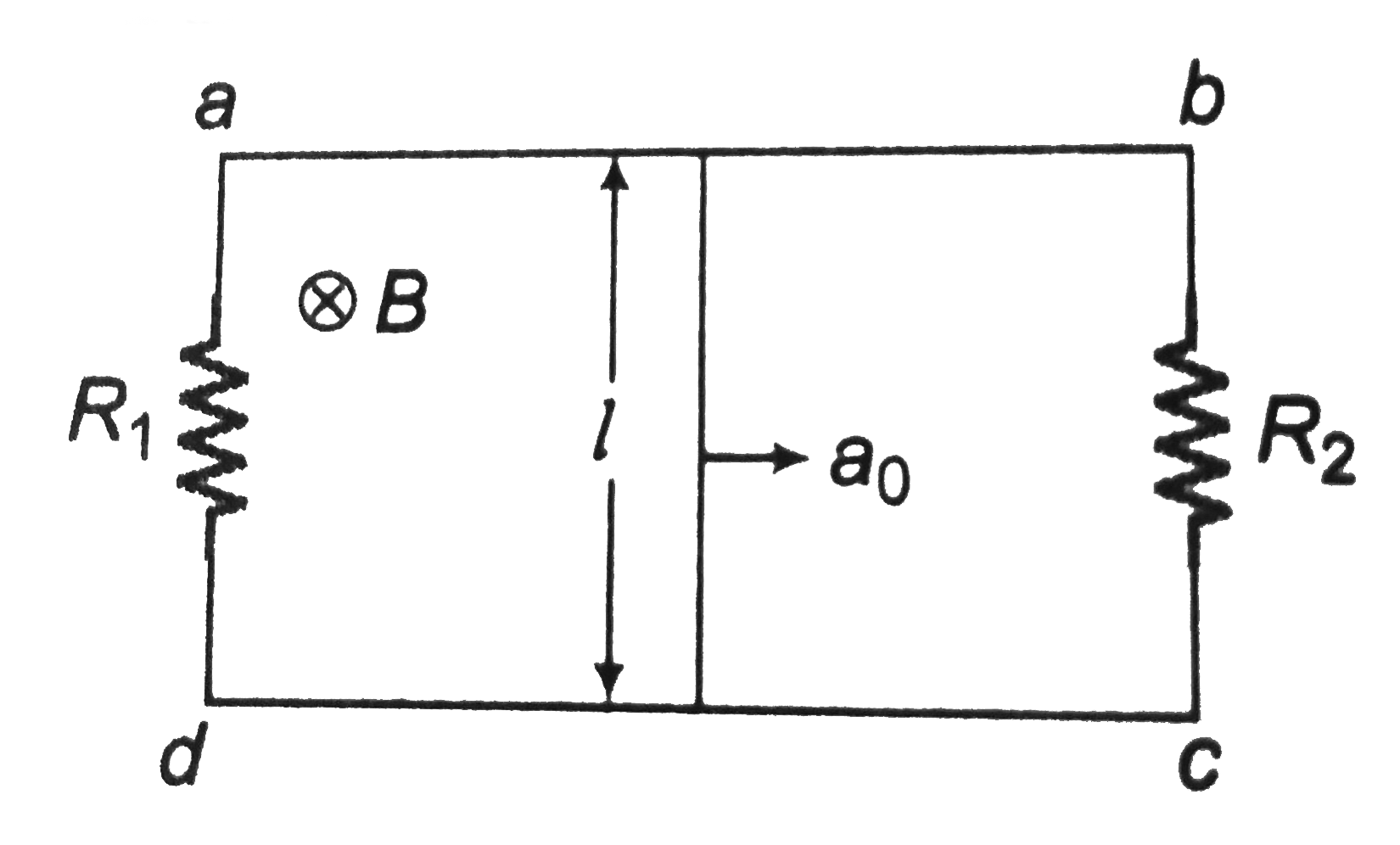
(a) the current through the conductor during its motion.
(b) the polarity of abcd terminal.
(c) external force required to move the conductor with the given acceleration.
View Solutiona conducting loop of radius R is precent in a uniform magnetic-field B perpendicular the plane of the ring. If radius R varies as a function of time 't', as R0+t. The e.m.f induced in the loop is

View Solution
