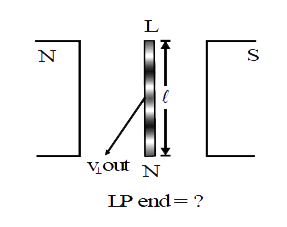A straight conductor 0.1 m long moves in a uniform magnetic field 0.1 T. The velocity of the conductor is 15ms−1 and is directed perpendicular to the field. The emf induced between the two ends of the conductor is
0.10 V
0.15 V
1.50 V
15 V
The correct Answer is:B
To find the induced electromotive force (emf) in a straight conductor moving in a magnetic field, we can use the formula for motional emf:
emf(E)=B⋅l⋅v⋅sin(θ)
Where:
- E is the induced emf,
- B is the magnetic field strength,
- l is the length of the conductor,
- v is the velocity of the conductor,
- θ is the angle between the direction of motion and the magnetic field.
1. Identify the given values:
- Length of the conductor, l=0.1m
- Magnetic field strength, B=0.1T
- Velocity of the conductor, v=15m/s
- Angle θ=90∘ (since the conductor moves perpendicular to the magnetic field)
2. Substitute the values into the formula:
Since the angle θ is 90∘, sin(90∘)=1. Therefore, the formula simplifies to:
E=B⋅l⋅v
3. Calculate the induced emf:
E=0.1T⋅0.1m⋅15m/s
E=0.1⋅0.1⋅15=0.15V
4. Conclusion:
The induced emf between the two ends of the conductor is 0.15V.
Final Answer:
The induced emf is 0.15V.
---
- E is the induced emf,
- B is the magnetic field strength,
- l is the length of the conductor,
- v is the velocity of the conductor,
- θ is the angle between the direction of motion and the magnetic field.
- Length of the conductor, l=0.1m
- Magnetic field strength, B=0.1T
- Velocity of the conductor, v=15m/s
- Angle θ=90∘ (since the conductor moves perpendicular to the magnetic field)
Since the angle θ is 90∘, sin(90∘)=1. Therefore, the formula simplifies to:
E=B⋅l⋅v
E=0.1T⋅0.1m⋅15m/s
E=0.1⋅0.1⋅15=0.15V
The induced emf between the two ends of the conductor is 0.15V.
The induced emf is 0.15V.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBook:DC PANDEYChapter:ELECTROMAGNETIC INDUCTIONExercise:Match the columns
Explore 5 Videos
- CURRENT ELECTRICITYBook:DC PANDEYChapter:CURRENT ELECTRICITYExercise:Medical entrances gallery
Explore 97 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEYChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
Similar Questions
Knowledge Check
A straight conductor 0.1 m long moves in a uniform magnetic field 0.1 T. The velocity of the conductor is 15 m/s and is directed perpendicular to the field. The e.m.f. induced between the two ends of the conductor is
A0.10 VB0.15 VC1.50 VD15.00 VA straight conductor of length 1.5m moves in a uniform magnetic field of induction 5×10−3T with a velocity of 5m/s in a direction perpendicular to its length and also perpendicular to the field. The e.m.f. induced between the ends of the conductor is
A1.5×10−3VB3.75×10−3VC37.5×10−3VD25×10−3V
When straight conductor moves in external magnetic field (LHP rule):-
View SolutionWhen straight conductor moves in external magnetic field (LHP rule):-
View SolutionWhen straight conductor moves in external magnetic field (LHP rule):-
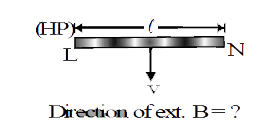
View SolutionWhen straight conductor moves in external magnetic field (LHP rule):-
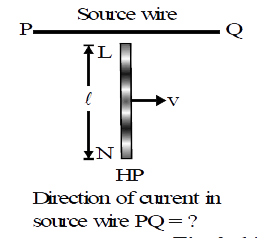
View SolutionWhen straight conductor moves in external magnetic field (LHP rule):-

View SolutionA conductor is moving with velocity v in a region of uniform magnetic field B.The electric field at P inside conductor is
View Solution