A square loop of edge b having M turns is rotated with a uniform angular velocity ω about one of its diagonals which is kept fixed in a horizontal position. A uniform magnetic field B0 exists in the vertical direction.
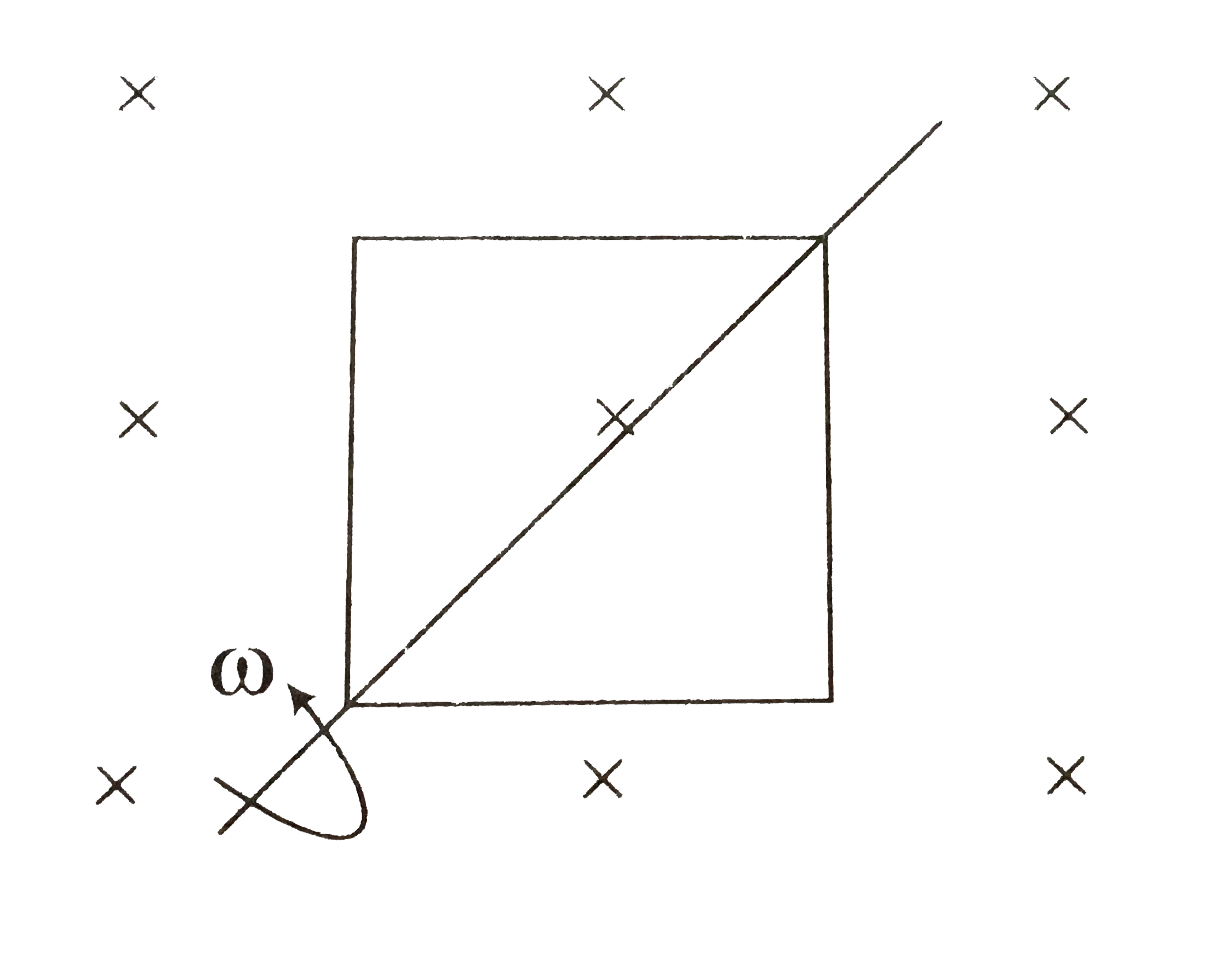
Find (i) the emf induced in the coil as a function of time t.
(ii) the maximum emf induced.
(iii) the average emf induced in the loop over a long period.
(iv) if resistance of loop is R, amount of charge flown in time t = 0 to t = 2T.
(v) heat produced in time t = 0 to t = 2T.
Initially, plane of loop is ⊥ar to the field. Let at any time, normal to loop makes an angle θ with magnetic field θ=ωt.
The flux passing through loop,
ϕB=MB0Scosθ=MB0b2cosωt
⇒ e=−dϕBdt=MB0b2ωsinωt=e0sinωt,
where, e0=MB0b2ω
(ii) For emf to be maximum, then sin ωt should be equal to 1.
⇒ emax=e0
(iii) Long period means one time period, i.e., 0→T
We know that average emf is given as
¯e=∫T0edt∫T0dt=1T.e0∫T0sinωtdt=0 (∵∫T0sinωtdt=0)
(iv) Using the relation, induced current,
i=eR=e0Rsinωt=i0sinωt
where, i0=e0R.
We know q = idt
So, for time O→2T,
q=∫2T0idt=i0∫2T0sinωtdt=0
(v) Heat (H) generated in a loop during time 0→2T, is given as
H=∫2T0e2Rdt=e200∫2T0sin2ωtdt
=e20R.2.T2=e20R.2πω=2πe20ωR (∵T=2πω)
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 1
3 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 2
2 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery
97 Videos
- ELECTROMAGNETIC WAVESBOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C
22 Videos
Similar Questions
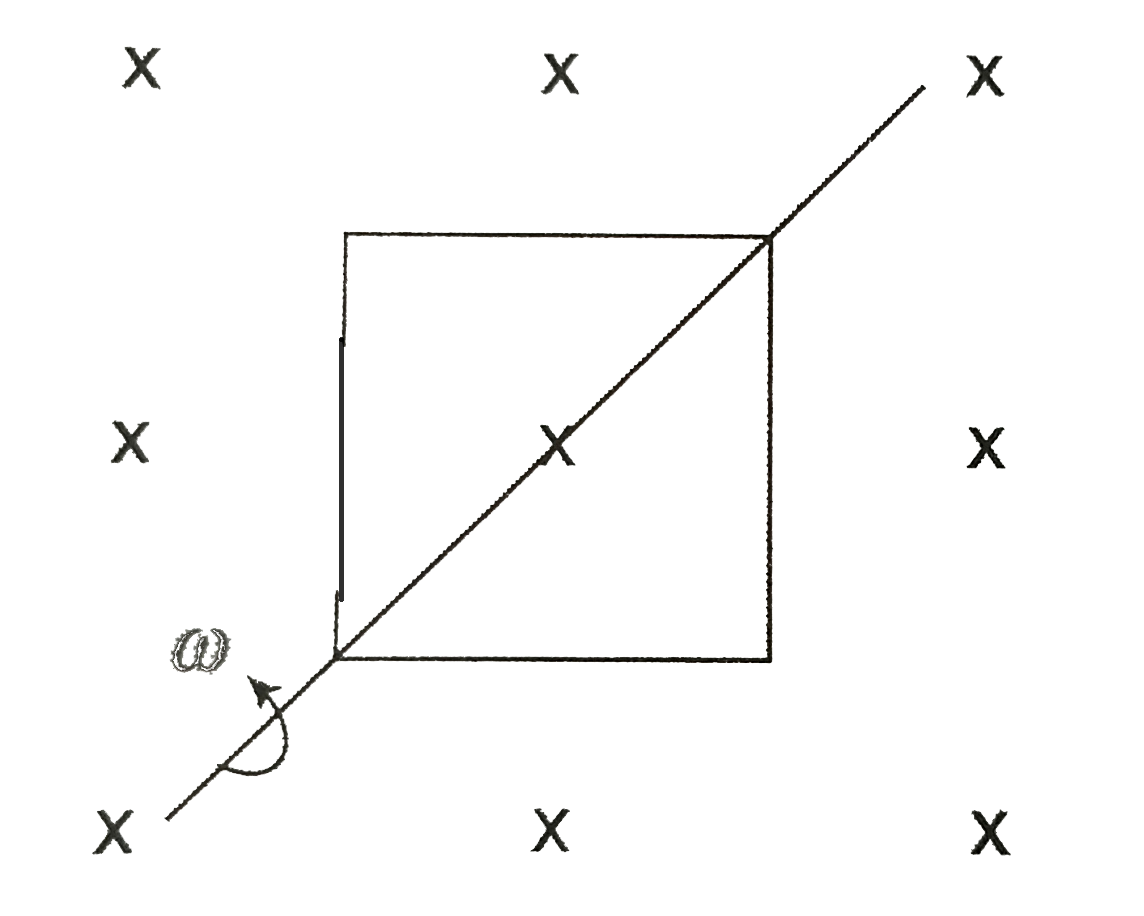
A square loop of edge a having N turns is rotated with a uniform angular velocity ω about one of its diagonals which is kept fixed in a horizontal position. A uniform magnetic field B exists in the vertical direction. Find
(a) the emf induced ion the coil as a function of time t
(b) the maximum emf induced
(c) the average emf induced in the loop over a long period (d) the average of the squares of emf induced over a long period
(e) if resistance of loop is R , amount of change flow in time t=0 to t=2T
(f) heat produced in time t=0 to =4T
View SolutionA ring rotates with angular velocity ω about an axis in the plane of the ring which passes through the center of the ring. A constant magnetic field B exists perpendicualr to the plane of the ring . Find the emf induced in the ring as a function of time.

View Solution
Knowledge Check
An emf induced in a coil rotating in a uniform magnetic field is given by
Ae=e0sinωtBe0=esinωtCe=sinωtDe=e0sinωA coil of N turns and mean area A is rotating with uniform angular velocity ω about an axis ai right angles to a uniform magnetic field B. The induced emfe in the coil will be
ANBAsinωtBNBωsinωtCNBAωsinωtDNBAωsinωtA coil of N turns and mean cross-sectional area A is rotating with uniform angular velocity ω about an axis at right angle to uniform magnetic field B. The induced emf E in the coil will be
ANBAsinωtBNBωsinωtCNB/AsinωtDNBAωsinωt
A wire loop confined in a plane is rotated in its oen plane with some angular velocity. A uniform magnetic field exists in the region. Fid the emf induced in the loop.
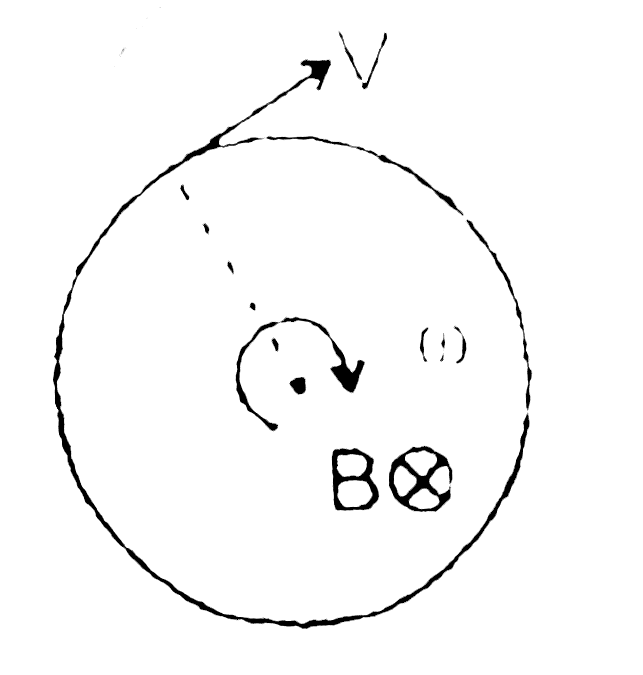
View SolutionA ring rotates with angular velocity ω about an axis perpendicula to the plane of the ring passing through the center of the ring (Fig. 3.77). A constant magnetic field B exists parallel to the axis. Find the emf induced in the ring.

View SolutionA ring rotates with angular velocity ω about an axis perpendicular to the plane of the ring passing through the center of the ring.A constant magnetic field B exists parallel to the axis.Find the emf induced in the ring.
View SolutionA circular coil of one turn of radiius 5.0 cm is rotated about a diameter with a constatn angular speed of 80 revolutions per minute. A uniform magnetic field B =0.010 T exists in a directon perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c ) the average of the squares of emf induced over a long period.
View SolutionA circular coil of one turn of radius 5.0cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B=0.0IT exists in a direction perpendicular to the axis of rotation, the maximum emf induced, the average emf induced in the coil over a long period and the average of the squares of emf induced over a long period is
View Solution
