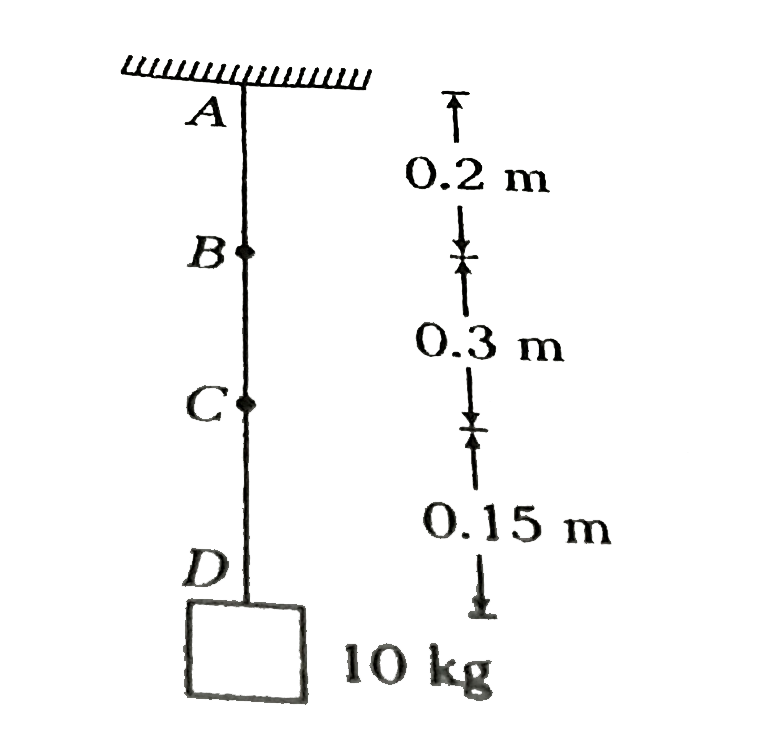
A rod AD consisting of three segments AB,BC and CD joined together is hanging vertically from a fixed support at A. The lengths of the segments are restectively 0.2 m , 0.3m and 0.15 m . The cross-section of the rod is uniformly 10−4m2 . A weight of 10 kg is hung from D.Calculate the displacement of points B,C and D if YAB=3.5×1010Nm−2,YBC=5×1010,YCD=2×1010Nm−2.
(Neglect the weight of the rod )
Given, area , A=10−14m2
YAB=3.5×1010Nm−2
YBC=5×1010Nm−2
YCD=2×1010Nm−2
Increase in length,
ΔL=FLAY=MgLAY=10×10L10−4Y=106LY
Now, increase in length of AB segment
(ΔLAB)=106×LABYAB=106×23.5×1010=5.7×10−6m
Increase in length of BC segment
(ΔL)BC=106×LBCYBC
=106×0.35×1010=6×10−6m
Increase in length of CD segment
(ΔL)CD=106LCDYCD=106×(0.15)×(2×1010)=7.5×10−6m
So, Displacement of B=LAB=5.7×10−6m
Displacement of C=ΔLAB+ΔLBC=11.7×10−6m
Displacement of D=ΔLAB+ΔLBC+ΔLCD=26.7×10−6m
Topper's Solved these Questions
- ELASTICITYBook:DC PANDEYChapter:ELASTICITYExercise:Check point 12.1
Explore 15 Videos
- ELASTICITYBook:DC PANDEYChapter:ELASTICITYExercise:Check point 12.2
Explore 15 Videos
- ELASTICITYBook:DC PANDEYChapter:ELASTICITYExercise:Level 2 Subjective
Explore 10 Videos
- CURRENT ELECTRICITYBook:DC PANDEYChapter:CURRENT ELECTRICITYExercise:All Questions
Explore 434 Videos
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Integer
Explore 17 Videos
Similar Questions
A rod AD consisting of three segments AB, BC and CD joined together is hanging vertically from a fixed support at A. The lengths of the segments are respectively : 1 m, 0.2 m and 0.15 m. The cross section of the rod is uniformly 10–4m2. A weight of 10 kg is hung from D. Calculate the displacements of point of B, C and D using the data of Young's moduli given below (neglect the weight of the rod).
YAB=2.5×1010N/m2,
YBC=4.0×1010N/m2,
YCD=1.0×1010N/m2
View Solution(2.4×103)÷(8×10−2)=? 3×10−5 b. 3×104 c. 3×105 d. 30
View Solution
Knowledge Check
For a material Y=6.6×1010Nm2 and bulk modulus K=11×1010N/m2, then its Poisson's ratio is
A0.8B0.35C0.7D0.4For increasing the length by 0.5mm in a steel wire of length 4m and area of cross section 5mm2, the force required is (Y=11.90×1012N/m2)
A4×107NB2×103NC7.4×103ND103NA light rod of length 2 m is suspended ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is ade of steel and is of cross-section 0.1 cm and the other of brass of cross-section 0.2 cm. Along the rod at what distance a weight may be hung to produce stresses in the wires?
(YSteel=2×1011Nm−2,YBass=1×1011Nm−2)A43m from steel wireB43m from brass wireC1 m from steel wireD14m from brass wire
A wire of length 1m is stretched by a force of 10N. The area of cross-section of the wire is 2×10–6m2 and Y is 2×1011N/m2 . Increase in length of the wire will be -
View SolutionWhen a force is applied on a wire of uniform cross-sectional are 3×10−6m2 and length 4 m, the increase in length is 1 mm. Energy stored in it will be (Given, Y=2×1011Nm−2)
View SolutionOn increasing the length by 0.5 mm in a steel wire of length 2 m and area of cross section 2mm2, the force required is [Y for steel =2.2×1011Nm2]
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
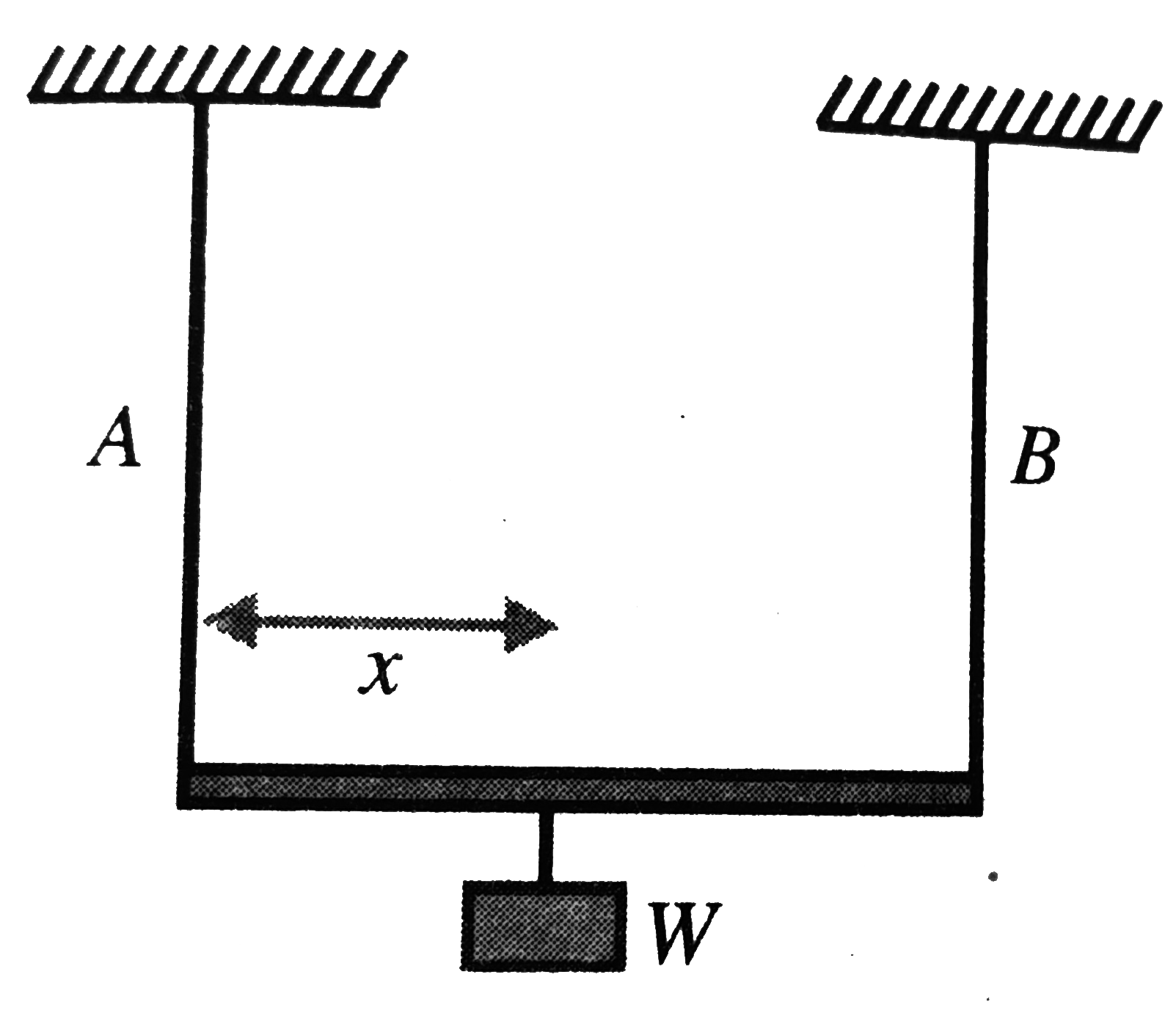
Determine the value of x so that equal strains are produced in each wire
View SolutionA light rod of length L=2m is suspended horizontally from the ceiling by two wires A and B of equal lengths. The wire A is made of steel with the area of cross section AS=1×10−5m2, while the wire B is made of brass of cross sectional area Ab=2×10−5m2. A weight W is suspended at a distance x from the wire A as shown in figure.
Take, Young's modulus of steel and brass as Ys=2×1011Nm−2 and Yb=1×1011Nm−2.
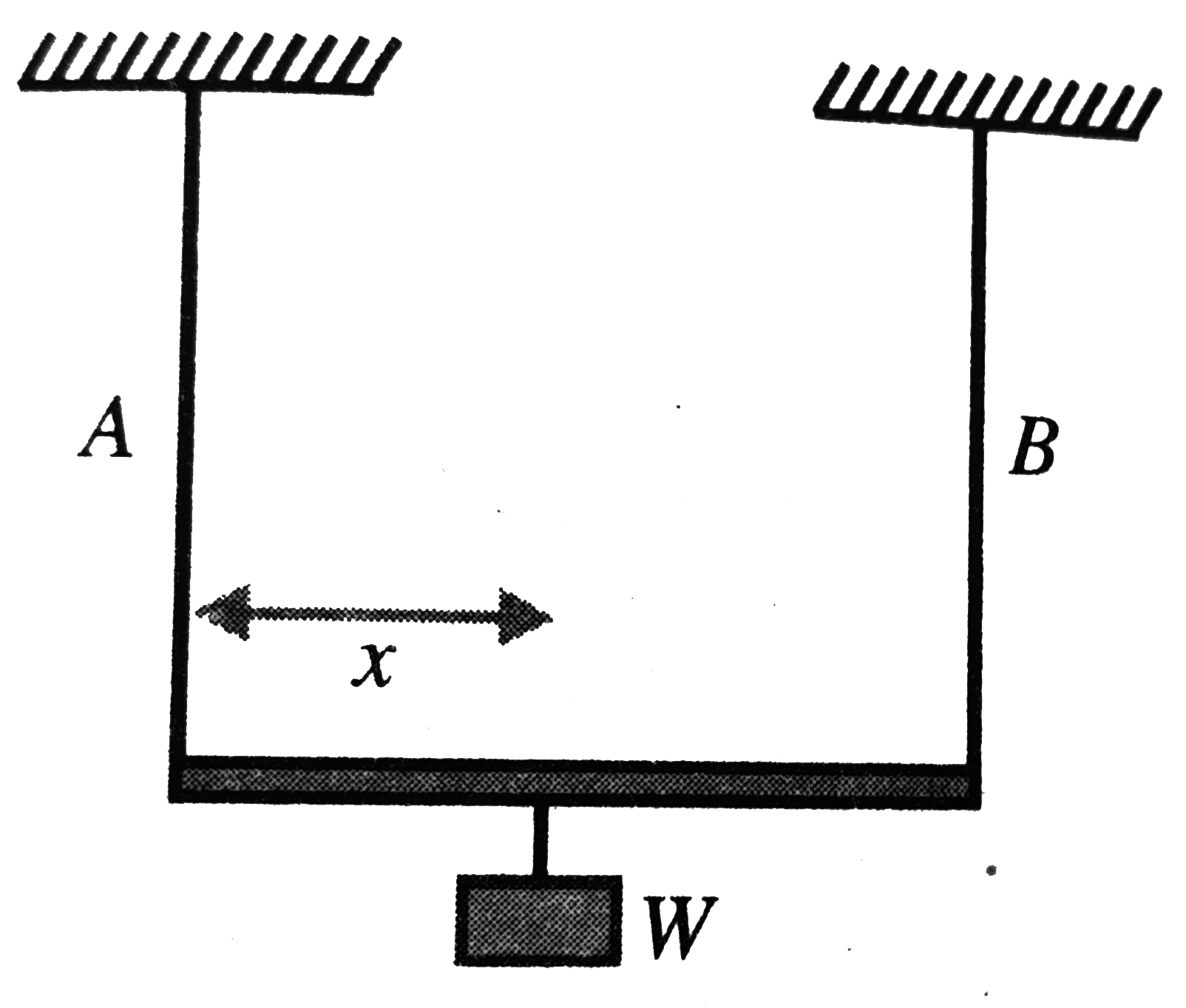
Determine the value of x so that equal stresses are produced in each wire.
View Solution
