The velocity v and displacement x of a particle executing simple harmonic motion are related as
vdvdx=−ω2x.
Atx=0,v=v0. Find the velocity v when the displacement becomes x.
√v20+ω2x2
√v20−ω2x2
v=3√v30+ω2x3
v=v0−(ω3x3ex3)1/3
The correct Answer is:B
(b) Given, vdvdx=−ω2x
On integrating within the limitv∫v0vdv=x−0ω2xdx
⇒[v22]vv0=−ω2[x22]x0
⇒v2−v20=−ω2x2⇒v=√v20−ω2x2
Similar Questions
The plot of velocity (v) versus displacement (x) of a particle executing simple harmonic motion is shown in figure. The time period of oscillation of particle is :-

View SolutionThe velocity-displacement graph of a particle is shown in the figure. Write the relation/equation between v and x.
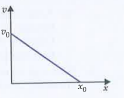 .
.
View Solution
Knowledge Check
The total energy of a particle having a displacement x, executing simple harmonic motion is
A∝xB∝x2Cindependent of xD∝x1/2A particle executing simple harmonic motion with an amplitude 5 cm and a time period 0.2 s. the velocity and acceleration of the particle when the displacement is 5 cm is
A0.5πms−1,0ms−2B0.5ms−1,−5π2ms−2C0ms−1,−5π2ms−2D0.5πms−1,−0.5π2ms−2If the displacement (x) and velocity (v) of a particle executing simple harmonic motion are related through the expression 4v2=25−x2, then its time period is given by
AπB2πC4πD6π
The acceleration-displacement (a−X) graph of a particle executing simple harmonic motion is shown in the figure. Find the frequency of oscillation.

View SolutionThe energy of a particle executing simple harmonic motion is given by E=Ax2+Bv2 where x is the displacement from mean position x=0 and v is the velocity of the particle at x then choose the correct statement(s)
View SolutionIf x,v and a denote the displacement, the velocity and the acceleration of a particle executing simple harmonic motion of time period T, then, which of the following does not change with time ?
View SolutionThe figure shows graph between velocity 'V' and displacement 'X' from mean position of a particle performing simple harmonic motion

The velocity of particle when it is at a distance 1.5m from mean position is :
View SolutionThe equation of motion of a particle executing simple harmonic motion is a+16π2x=0 In this equation, a is the linear acceleration in m/s2 of the particle at a displacement x in meter. The time period in simple harmonic motion is
View Solution